A Simulation-Free Deep Learning Approach to Stochastic Optimal Control

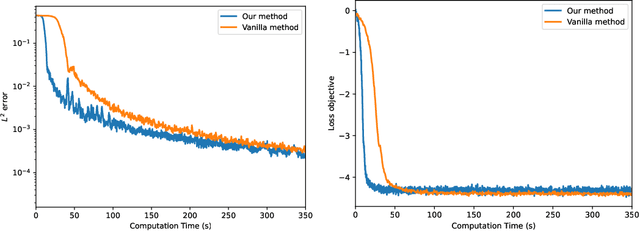
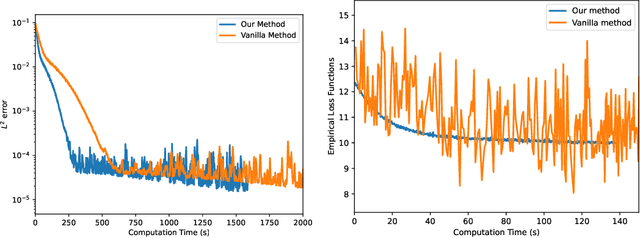
We propose a simulation-free algorithm for the solution of generic problems in stochastic optimal control (SOC). Unlike existing methods, our approach does not require the solution of an adjoint problem, but rather leverages Girsanov theorem to directly calculate the gradient of the SOC objective on-policy. This allows us to speed up the optimization of control policies parameterized by neural networks since it completely avoids the expensive back-propagation step through stochastic differential equations (SDEs) used in the Neural SDE framework. In particular, it enables us to solve SOC problems in high dimension and on long time horizons. We demonstrate the efficiency of our approach in various domains of applications, including standard stochastic optimal control problems, sampling from unnormalized distributions via construction of a Schr\"odinger-F\"ollmer process, and fine-tuning of pre-trained diffusion models. In all cases our method is shown to outperform the existing methods in both the computing time and memory efficiency.

Probabilistic Forecasting with Stochastic Interpolants and Föllmer Processes

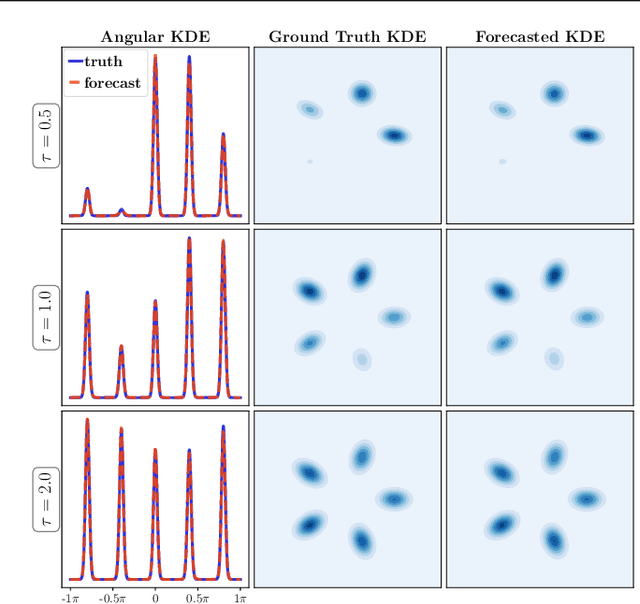
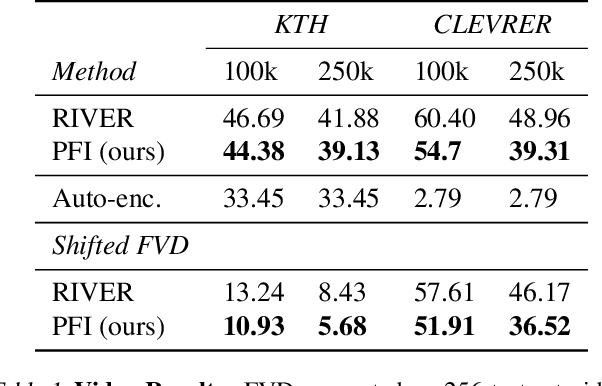
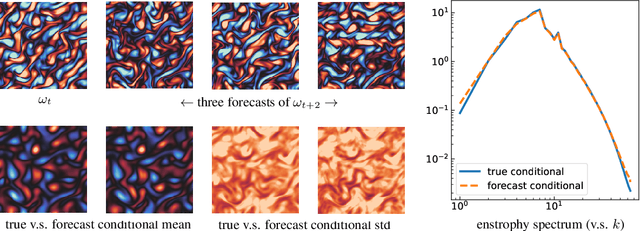
We propose a framework for probabilistic forecasting of dynamical systems based on generative modeling. Given observations of the system state over time, we formulate the forecasting problem as sampling from the conditional distribution of the future system state given its current state. To this end, we leverage the framework of stochastic interpolants, which facilitates the construction of a generative model between an arbitrary base distribution and the target. We design a fictitious, non-physical stochastic dynamics that takes as initial condition the current system state and produces as output a sample from the target conditional distribution in finite time and without bias. This process therefore maps a point mass centered at the current state onto a probabilistic ensemble of forecasts. We prove that the drift coefficient entering the stochastic differential equation (SDE) achieving this task is non-singular, and that it can be learned efficiently by square loss regression over the time-series data. We show that the drift and the diffusion coefficients of this SDE can be adjusted after training, and that a specific choice that minimizes the impact of the estimation error gives a F\"ollmer process. We highlight the utility of our approach on several complex, high-dimensional forecasting problems, including stochastically forced Navier-Stokes and video prediction on the KTH and CLEVRER datasets.

Efficient Training of Energy-Based Models Using Jarzynski Equality

Energy-based models (EBMs) are generative models inspired by statistical physics with a wide range of applications in unsupervised learning. Their performance is best measured by the cross-entropy (CE) of the model distribution relative to the data distribution. Using the CE as the objective for training is however challenging because the computation of its gradient with respect to the model parameters requires sampling the model distribution. Here we show how results for nonequilibrium thermodynamics based on Jarzynski equality together with tools from sequential Monte-Carlo sampling can be used to perform this computation efficiently and avoid the uncontrolled approximations made using the standard contrastive divergence algorithm. Specifically, we introduce a modification of the unadjusted Langevin algorithm (ULA) in which each walker acquires a weight that enables the estimation of the gradient of the cross-entropy at any step during GD, thereby bypassing sampling biases induced by slow mixing of ULA. We illustrate these results with numerical experiments on Gaussian mixture distributions as well as the MNIST dataset. We show that the proposed approach outperforms methods based on the contrastive divergence algorithm in all the considered situations.