Contrasting with Symile: Simple Model-Agnostic Representation Learning for Unlimited Modalities

Contrastive learning methods, such as CLIP, leverage naturally paired data-for example, images and their corresponding text captions-to learn general representations that transfer efficiently to downstream tasks. While such approaches are generally applied to two modalities, domains such as robotics, healthcare, and video need to support many types of data at once. We show that the pairwise application of CLIP fails to capture joint information between modalities, thereby limiting the quality of the learned representations. To address this issue, we present Symile, a simple contrastive learning approach that captures higher-order information between any number of modalities. Symile provides a flexible, architecture-agnostic objective for learning modality-specific representations. To develop Symile's objective, we derive a lower bound on total correlation, and show that Symile representations for any set of modalities form a sufficient statistic for predicting the remaining modalities. Symile outperforms pairwise CLIP, even with modalities missing in the data, on cross-modal classification and retrieval across several experiments including on an original multilingual dataset of 33M image, text and audio samples and a clinical dataset of chest X-rays, electrocardiograms, and laboratory measurements. All datasets and code used in this work are publicly available at https://github.com/rajesh-lab/symile.

What's the score? Automated Denoising Score Matching for Nonlinear Diffusions

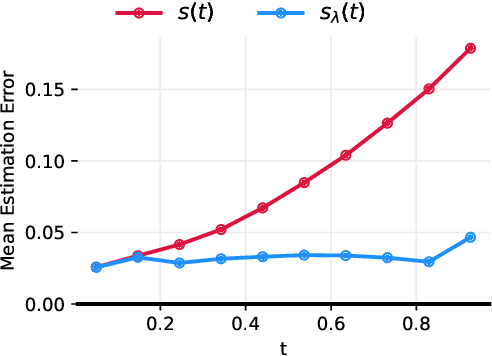
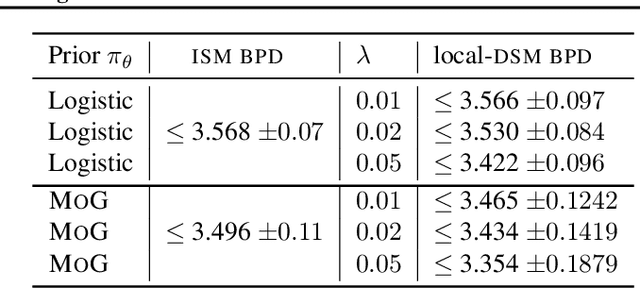
Reversing a diffusion process by learning its score forms the heart of diffusion-based generative modeling and for estimating properties of scientific systems. The diffusion processes that are tractable center on linear processes with a Gaussian stationary distribution. This limits the kinds of models that can be built to those that target a Gaussian prior or more generally limits the kinds of problems that can be generically solved to those that have conditionally linear score functions. In this work, we introduce a family of tractable denoising score matching objectives, called local-DSM, built using local increments of the diffusion process. We show how local-DSM melded with Taylor expansions enables automated training and score estimation with nonlinear diffusion processes. To demonstrate these ideas, we use automated-DSM to train generative models using non-Gaussian priors on challenging low dimensional distributions and the CIFAR10 image dataset. Additionally, we use the automated-DSM to learn the scores for nonlinear processes studied in statistical physics.

Probabilistic Forecasting with Stochastic Interpolants and Föllmer Processes

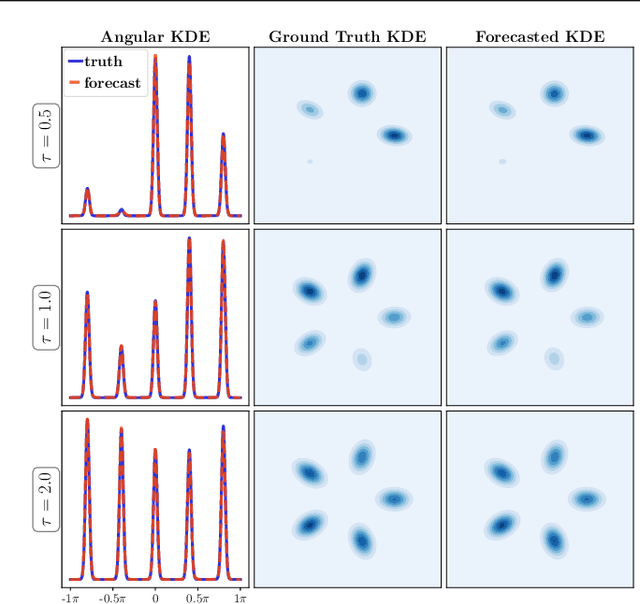
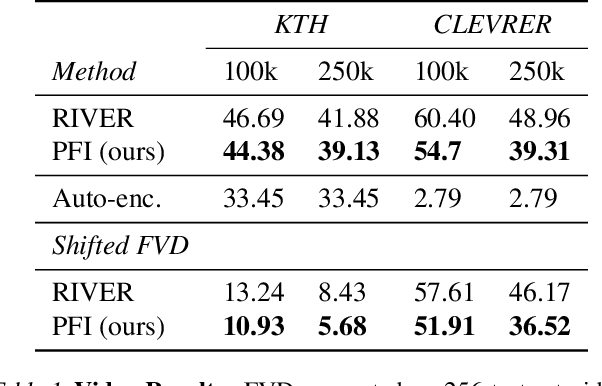
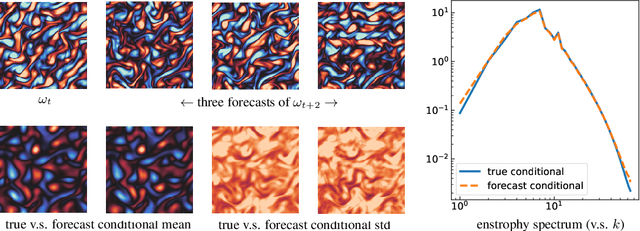
We propose a framework for probabilistic forecasting of dynamical systems based on generative modeling. Given observations of the system state over time, we formulate the forecasting problem as sampling from the conditional distribution of the future system state given its current state. To this end, we leverage the framework of stochastic interpolants, which facilitates the construction of a generative model between an arbitrary base distribution and the target. We design a fictitious, non-physical stochastic dynamics that takes as initial condition the current system state and produces as output a sample from the target conditional distribution in finite time and without bias. This process therefore maps a point mass centered at the current state onto a probabilistic ensemble of forecasts. We prove that the drift coefficient entering the stochastic differential equation (SDE) achieving this task is non-singular, and that it can be learned efficiently by square loss regression over the time-series data. We show that the drift and the diffusion coefficients of this SDE can be adjusted after training, and that a specific choice that minimizes the impact of the estimation error gives a F\"ollmer process. We highlight the utility of our approach on several complex, high-dimensional forecasting problems, including stochastically forced Navier-Stokes and video prediction on the KTH and CLEVRER datasets.

SiT: Exploring Flow and Diffusion-based Generative Models with Scalable Interpolant Transformers

We present Scalable Interpolant Transformers (SiT), a family of generative models built on the backbone of Diffusion Transformers (DiT). The interpolant framework, which allows for connecting two distributions in a more flexible way than standard diffusion models, makes possible a modular study of various design choices impacting generative models built on dynamical transport: using discrete vs. continuous time learning, deciding the objective for the model to learn, choosing the interpolant connecting the distributions, and deploying a deterministic or stochastic sampler. By carefully introducing the above ingredients, SiT surpasses DiT uniformly across model sizes on the conditional ImageNet 256x256 benchmark using the exact same backbone, number of parameters, and GFLOPs. By exploring various diffusion coefficients, which can be tuned separately from learning, SiT achieves an FID-50K score of 2.06.

Stochastic interpolants with data-dependent couplings

Generative models inspired by dynamical transport of measure -- such as flows and diffusions -- construct a continuous-time map between two probability densities. Conventionally, one of these is the target density, only accessible through samples, while the other is taken as a simple base density that is data-agnostic. In this work, using the framework of stochastic interpolants, we formalize how to \textit{couple} the base and the target densities. This enables us to incorporate information about class labels or continuous embeddings to construct dynamical transport maps that serve as conditional generative models. We show that these transport maps can be learned by solving a simple square loss regression problem analogous to the standard independent setting. We demonstrate the usefulness of constructing dependent couplings in practice through experiments in super-resolution and in-painting.

A dynamic risk score for early prediction of cardiogenic shock using machine learning

Myocardial infarction and heart failure are major cardiovascular diseases that affect millions of people in the US. The morbidity and mortality are highest among patients who develop cardiogenic shock. Early recognition of cardiogenic shock is critical. Prompt implementation of treatment measures can prevent the deleterious spiral of ischemia, low blood pressure, and reduced cardiac output due to cardiogenic shock. However, early identification of cardiogenic shock has been challenging due to human providers' inability to process the enormous amount of data in the cardiac intensive care unit (ICU) and lack of an effective risk stratification tool. We developed a deep learning-based risk stratification tool, called CShock, for patients admitted into the cardiac ICU with acute decompensated heart failure and/or myocardial infarction to predict onset of cardiogenic shock. To develop and validate CShock, we annotated cardiac ICU datasets with physician adjudicated outcomes. CShock achieved an area under the receiver operator characteristic curve (AUROC) of 0.820, which substantially outperformed CardShock (AUROC 0.519), a well-established risk score for cardiogenic shock prognosis. CShock was externally validated in an independent patient cohort and achieved an AUROC of 0.800, demonstrating its generalizability in other cardiac ICUs.

Where to Diffuse, How to Diffuse, and How to Get Back: Automated Learning for Multivariate Diffusions

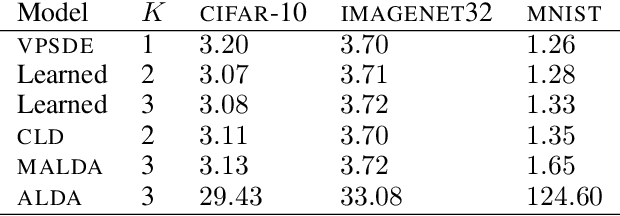
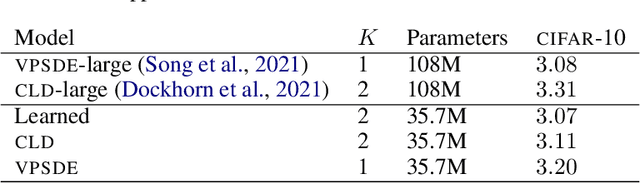
Diffusion-based generative models (DBGMs) perturb data to a target noise distribution and reverse this inference diffusion process to generate samples. The choice of inference diffusion affects both likelihoods and sample quality. For example, extending the inference process with auxiliary variables leads to improved sample quality. While there are many such multivariate diffusions to explore, each new one requires significant model-specific analysis, hindering rapid prototyping and evaluation. In this work, we study Multivariate Diffusion Models (MDMs). For any number of auxiliary variables, we provide a recipe for maximizing a lower-bound on the MDMs likelihood without requiring any model-specific analysis. We then demonstrate how to parameterize the diffusion for a specified target noise distribution; these two points together enable optimizing the inference diffusion process. Optimizing the diffusion expands easy experimentation from just a few well-known processes to an automatic search over all linear diffusions. To demonstrate these ideas, we introduce two new specific diffusions as well as learn a diffusion process on the MNIST, CIFAR10, and ImageNet32 datasets. We show learned MDMs match or surpass bits-per-dims (BPDs) relative to fixed choices of diffusions for a given dataset and model architecture.

Survival Mixture Density Networks

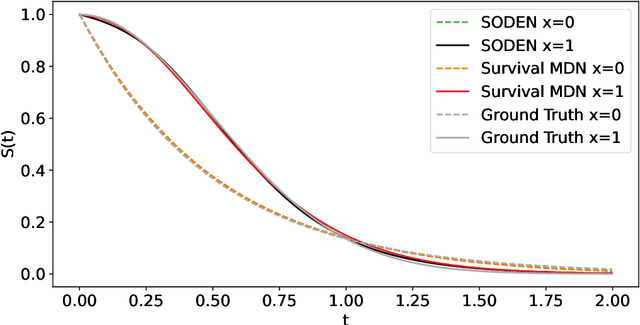
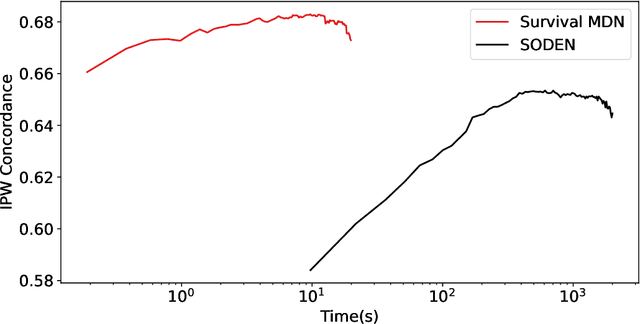
Survival analysis, the art of time-to-event modeling, plays an important role in clinical treatment decisions. Recently, continuous time models built from neural ODEs have been proposed for survival analysis. However, the training of neural ODEs is slow due to the high computational complexity of neural ODE solvers. Here, we propose an efficient alternative for flexible continuous time models, called Survival Mixture Density Networks (Survival MDNs). Survival MDN applies an invertible positive function to the output of Mixture Density Networks (MDNs). While MDNs produce flexible real-valued distributions, the invertible positive function maps the model into the time-domain while preserving a tractable density. Using four datasets, we show that Survival MDN performs better than, or similarly to continuous and discrete time baselines on concordance, integrated Brier score and integrated binomial log-likelihood. Meanwhile, Survival MDNs are also faster than ODE-based models and circumvent binning issues in discrete models.

Learning Invariant Representations with Missing Data

Spurious correlations allow flexible models to predict well during training but poorly on related test populations. Recent work has shown that models that satisfy particular independencies involving correlation-inducing \textit{nuisance} variables have guarantees on their test performance. Enforcing such independencies requires nuisances to be observed during training. However, nuisances, such as demographics or image background labels, are often missing. Enforcing independence on just the observed data does not imply independence on the entire population. Here we derive \acrshort{mmd} estimators used for invariance objectives under missing nuisances. On simulations and clinical data, optimizing through these estimates achieves test performance similar to using estimators that make use of the full data.

Inverse-Weighted Survival Games

Deep models trained through maximum likelihood have achieved state-of-the-art results for survival analysis. Despite this training scheme, practitioners evaluate models under other criteria, such as binary classification losses at a chosen set of time horizons, e.g. Brier score (BS) and Bernoulli log likelihood (BLL). Models trained with maximum likelihood may have poor BS or BLL since maximum likelihood does not directly optimize these criteria. Directly optimizing criteria like BS requires inverse-weighting by the censoring distribution, estimation of which itself also requires inverse-weighted by the failure distribution. But neither are known. To resolve this dilemma, we introduce Inverse-Weighted Survival Games to train both failure and censoring models with respect to criteria such as BS or BLL. In these games, objectives for each model are built from re-weighted estimates featuring the other model, where the re-weighting model is held fixed during training. When the loss is proper, we show that the games always have the true failure and censoring distributions as a stationary point. This means models in the game do not leave the correct distributions once reached. We construct one case where this stationary point is unique. We show that these games optimize BS on simulations and then apply these principles on real world cancer and critically-ill patient data.