Sublinear iterations can suffice even for DDPMs

SDE-based methods such as denoising diffusion probabilistic models (DDPMs) have shown remarkable success in real-world sample generation tasks. Prior analyses of DDPMs have been focused on the exponential Euler discretization, showing guarantees that generally depend at least linearly on the dimension or initial Fisher information. Inspired by works in log-concave sampling (Shen and Lee, 2019), we analyze an integrator -- the denoising diffusion randomized midpoint method (DDRaM) -- that leverages an additional randomized midpoint to better approximate the SDE. Using a recently-developed analytic framework called the "shifted composition rule", we show that this algorithm enjoys favorable discretization properties under appropriate smoothness assumptions, with sublinear $\widetilde{O}(\sqrt{d})$ score evaluations needed to ensure convergence. This is the first sublinear complexity bound for pure DDPM sampling -- prior works which obtained such bounds worked instead with ODE-based sampling and had to make modifications to the sampler which deviate from how they are used in practice. We also provide experimental validation of the advantages of our method, showing that it performs well in practice with pre-trained image synthesis models.

Generalised Flow Maps for Few-Step Generative Modelling on Riemannian Manifolds

Geometric data and purpose-built generative models on them have become ubiquitous in high-impact deep learning application domains, ranging from protein backbone generation and computational chemistry to geospatial data. Current geometric generative models remain computationally expensive at inference -- requiring many steps of complex numerical simulation -- as they are derived from dynamical measure transport frameworks such as diffusion and flow-matching on Riemannian manifolds. In this paper, we propose Generalised Flow Maps (GFM), a new class of few-step generative models that generalises the Flow Map framework in Euclidean spaces to arbitrary Riemannian manifolds. We instantiate GFMs with three self-distillation-based training methods: Generalised Lagrangian Flow Maps, Generalised Eulerian Flow Maps, and Generalised Progressive Flow Maps. We theoretically show that GFMs, under specific design decisions, unify and elevate existing Euclidean few-step generative models, such as consistency models, shortcut models, and meanflows, to the Riemannian setting. We benchmark GFMs against other geometric generative models on a suite of geometric datasets, including geospatial data, RNA torsion angles, and hyperbolic manifolds, and achieve state-of-the-art sample quality for single- and few-step evaluations, and superior or competitive log-likelihoods using the implicit probability flow.

BoltzNCE: Learning Likelihoods for Boltzmann Generation with Stochastic Interpolants and Noise Contrastive Estimation

Efficient sampling from the Boltzmann distribution defined by an energy function is a key challenge in modeling physical systems such as molecules. Boltzmann Generators tackle this by leveraging Continuous Normalizing Flows that transform a simple prior into a distribution that can be reweighted to match the Boltzmann distribution using sample likelihoods. However, obtaining likelihoods requires computing costly Jacobians during integration, making it impractical for large molecular systems. To overcome this, we propose learning the likelihood of the generated distribution via an energy-based model trained with noise contrastive estimation and score matching. By using stochastic interpolants to anneal between the prior and generated distributions, we combine both the objective functions to efficiently learn the density function. On the alanine dipeptide system, we demonstrate that our method yields free energy profiles and energy distributions comparable to those obtained with exact likelihoods. Additionally, we show that free energy differences between metastable states can be estimated accurately with orders-of-magnitude speedup.

How to build a consistency model: Learning flow maps via self-distillation

Building on the framework proposed in Boffi et al. (2024), we present a systematic approach for learning flow maps associated with flow and diffusion models. Flow map-based models, commonly known as consistency models, encompass recent efforts to improve the efficiency of generative models based on solutions to differential equations. By exploiting a relationship between the velocity field underlying a continuous-time flow and the instantaneous rate of change of the flow map, we show how to convert existing distillation schemes into direct training algorithms via self-distillation, eliminating the need for pre-trained models. We empirically evaluate several instantiations of our framework, finding that high-dimensional tasks like image synthesis benefit from objective functions that avoid temporal and spatial derivatives of the flow map, while lower-dimensional tasks can benefit from objectives incorporating higher-order derivatives to capture sharp features.

Model-free learning of probability flows: Elucidating the nonequilibrium dynamics of flocking

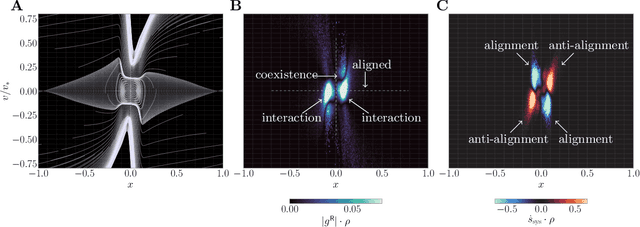
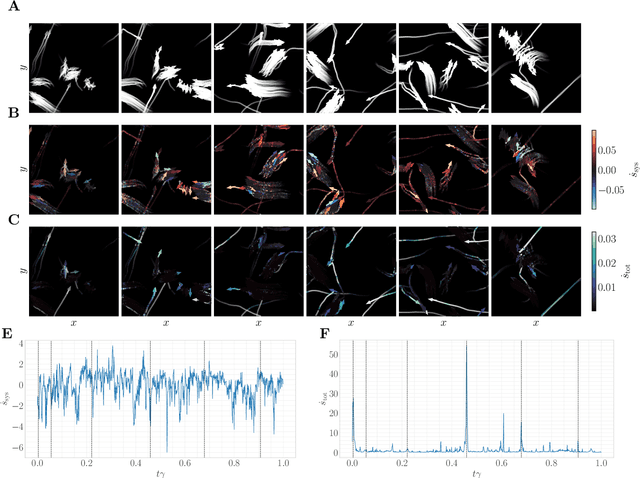
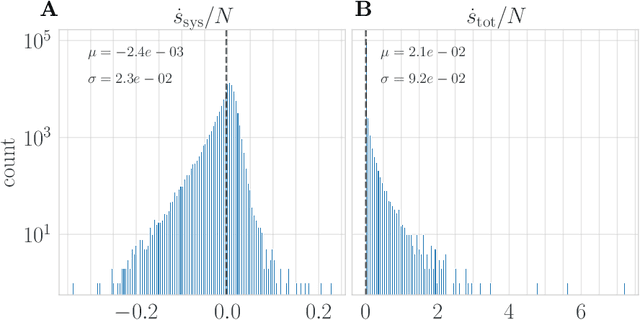
Active systems comprise a class of nonequilibrium dynamics in which individual components autonomously dissipate energy. Efforts towards understanding the role played by activity have centered on computation of the entropy production rate (EPR), which quantifies the breakdown of time reversal symmetry. A fundamental difficulty in this program is that high dimensionality of the phase space renders traditional computational techniques infeasible for estimating the EPR. Here, we overcome this challenge with a novel deep learning approach that estimates probability currents directly from stochastic system trajectories. We derive a new physical connection between the probability current and two local definitions of the EPR for inertial systems, which we apply to characterize the departure from equilibrium in a canonical model of flocking. Our results highlight that entropy is produced and consumed on the spatial interface of a flock as the interplay between alignment and fluctuation dynamically creates and annihilates order. By enabling the direct visualization of when and where a given system is out of equilibrium, we anticipate that our methodology will advance the understanding of a broad class of complex nonequilibrium dynamics.

Shallow diffusion networks provably learn hidden low-dimensional structure

Diffusion-based generative models provide a powerful framework for learning to sample from a complex target distribution. The remarkable empirical success of these models applied to high-dimensional signals, including images and video, stands in stark contrast to classical results highlighting the curse of dimensionality for distribution recovery. In this work, we take a step towards understanding this gap through a careful analysis of learning diffusion models over the Barron space of single layer neural networks. In particular, we show that these shallow models provably adapt to simple forms of low dimensional structure, thereby avoiding the curse of dimensionality. We combine our results with recent analyses of sampling with diffusion models to provide an end-to-end sample complexity bound for learning to sample from structured distributions. Importantly, our results do not require specialized architectures tailored to particular latent structures, and instead rely on the low-index structure of the Barron space to adapt to the underlying distribution.

Flow Map Matching

Generative models based on dynamical transport of measure, such as diffusion models, flow matching models, and stochastic interpolants, learn an ordinary or stochastic differential equation whose trajectories push initial conditions from a known base distribution onto the target. While training is cheap, samples are generated via simulation, which is more expensive than one-step models like GANs. To close this gap, we introduce flow map matching -- an algorithm that learns the two-time flow map of an underlying ordinary differential equation. The approach leads to an efficient few-step generative model whose step count can be chosen a-posteriori to smoothly trade off accuracy for computational expense. Leveraging the stochastic interpolant framework, we introduce losses for both direct training of flow maps and distillation from pre-trained (or otherwise known) velocity fields. Theoretically, we show that our approach unifies many existing few-step generative models, including consistency models, consistency trajectory models, progressive distillation, and neural operator approaches, which can be obtained as particular cases of our formalism. With experiments on CIFAR-10 and ImageNet 32x32, we show that flow map matching leads to high-quality samples with significantly reduced sampling cost compared to diffusion or stochastic interpolant methods.

Probabilistic Forecasting with Stochastic Interpolants and Föllmer Processes

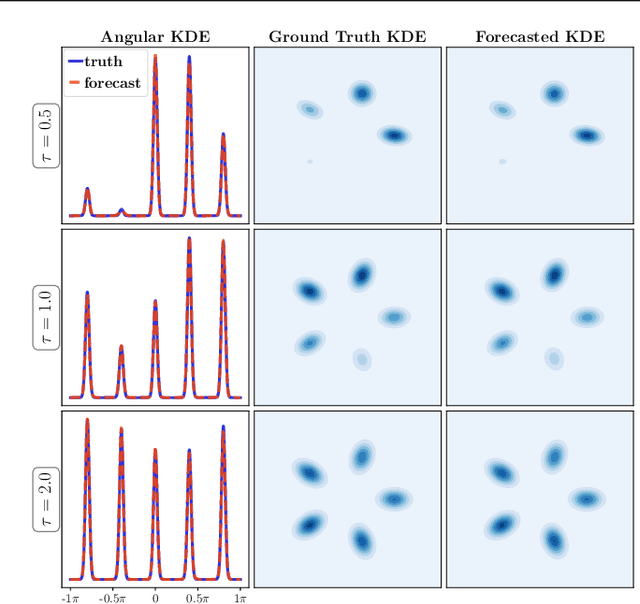
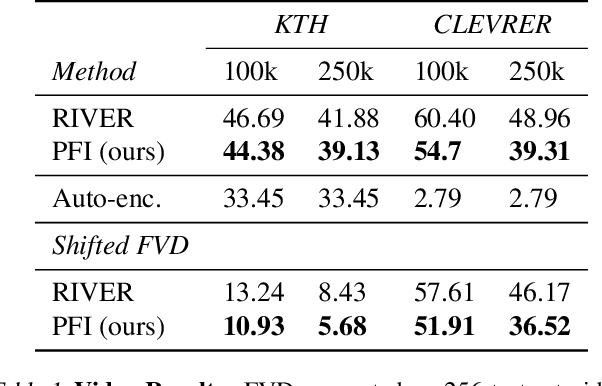
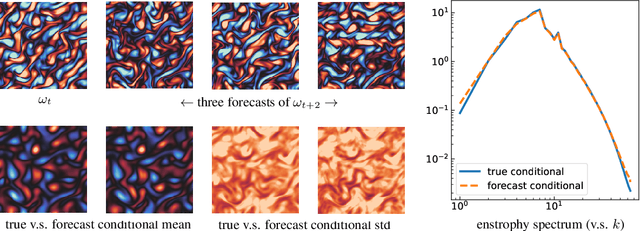
We propose a framework for probabilistic forecasting of dynamical systems based on generative modeling. Given observations of the system state over time, we formulate the forecasting problem as sampling from the conditional distribution of the future system state given its current state. To this end, we leverage the framework of stochastic interpolants, which facilitates the construction of a generative model between an arbitrary base distribution and the target. We design a fictitious, non-physical stochastic dynamics that takes as initial condition the current system state and produces as output a sample from the target conditional distribution in finite time and without bias. This process therefore maps a point mass centered at the current state onto a probabilistic ensemble of forecasts. We prove that the drift coefficient entering the stochastic differential equation (SDE) achieving this task is non-singular, and that it can be learned efficiently by square loss regression over the time-series data. We show that the drift and the diffusion coefficients of this SDE can be adjusted after training, and that a specific choice that minimizes the impact of the estimation error gives a F\"ollmer process. We highlight the utility of our approach on several complex, high-dimensional forecasting problems, including stochastically forced Navier-Stokes and video prediction on the KTH and CLEVRER datasets.

SiT: Exploring Flow and Diffusion-based Generative Models with Scalable Interpolant Transformers

We present Scalable Interpolant Transformers (SiT), a family of generative models built on the backbone of Diffusion Transformers (DiT). The interpolant framework, which allows for connecting two distributions in a more flexible way than standard diffusion models, makes possible a modular study of various design choices impacting generative models built on dynamical transport: using discrete vs. continuous time learning, deciding the objective for the model to learn, choosing the interpolant connecting the distributions, and deploying a deterministic or stochastic sampler. By carefully introducing the above ingredients, SiT surpasses DiT uniformly across model sizes on the conditional ImageNet 256x256 benchmark using the exact same backbone, number of parameters, and GFLOPs. By exploring various diffusion coefficients, which can be tuned separately from learning, SiT achieves an FID-50K score of 2.06.

Stochastic interpolants with data-dependent couplings

Generative models inspired by dynamical transport of measure -- such as flows and diffusions -- construct a continuous-time map between two probability densities. Conventionally, one of these is the target density, only accessible through samples, while the other is taken as a simple base density that is data-agnostic. In this work, using the framework of stochastic interpolants, we formalize how to \textit{couple} the base and the target densities. This enables us to incorporate information about class labels or continuous embeddings to construct dynamical transport maps that serve as conditional generative models. We show that these transport maps can be learned by solving a simple square loss regression problem analogous to the standard independent setting. We demonstrate the usefulness of constructing dependent couplings in practice through experiments in super-resolution and in-painting.