EX-DRL: Hedging Against Heavy Losses with EXtreme Distributional Reinforcement Learning

Recent advancements in Distributional Reinforcement Learning (DRL) for modeling loss distributions have shown promise in developing hedging strategies in derivatives markets. A common approach in DRL involves learning the quantiles of loss distributions at specified levels using Quantile Regression (QR). This method is particularly effective in option hedging due to its direct quantile-based risk assessment, such as Value at Risk (VaR) and Conditional Value at Risk (CVaR). However, these risk measures depend on the accurate estimation of extreme quantiles in the loss distribution's tail, which can be imprecise in QR-based DRL due to the rarity and extremity of tail data, as highlighted in the literature. To address this issue, we propose EXtreme DRL (EX-DRL), which enhances extreme quantile prediction by modeling the tail of the loss distribution with a Generalized Pareto Distribution (GPD). This method introduces supplementary data to mitigate the scarcity of extreme quantile observations, thereby improving estimation accuracy through QR. Comprehensive experiments on gamma hedging options demonstrate that EX-DRL improves existing QR-based models by providing more precise estimates of extreme quantiles, thereby improving the computation and reliability of risk metrics for complex financial risk management.

Deep Hedging of Derivatives Using Reinforcement Learning

This paper shows how reinforcement learning can be used to derive optimal hedging strategies for derivatives when there are transaction costs. The paper illustrates the approach by showing the difference between using delta hedging and optimal hedging for a short position in a call option when the objective is to minimize a function equal to the mean hedging cost plus a constant times the standard deviation of the hedging cost. Two situations are considered. In the first, the asset price follows a geometric Brownian motion. In the second, the asset price follows a stochastic volatility process. The paper extends the basic reinforcement learning approach in a number of ways. First, it uses two different Q-functions so that both the expected value of the cost and the expected value of the square of the cost are tracked for different state/action combinations. This approach increases the range of objective functions that can be used. Second, it uses a learning algorithm that allows for continuous state and action space. Third, it compares the accounting P&L approach (where the hedged position is valued at each step) and the cash flow approach (where cash inflows and outflows are used). We find that a hybrid approach involving the use of an accounting P&L approach that incorporates a relatively simple valuation model works well. The valuation model does not have to correspond to the process assumed for the underlying asset price.

Valuing Exotic Options and Estimating Model Risk

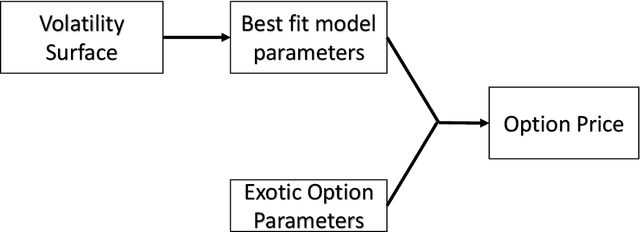
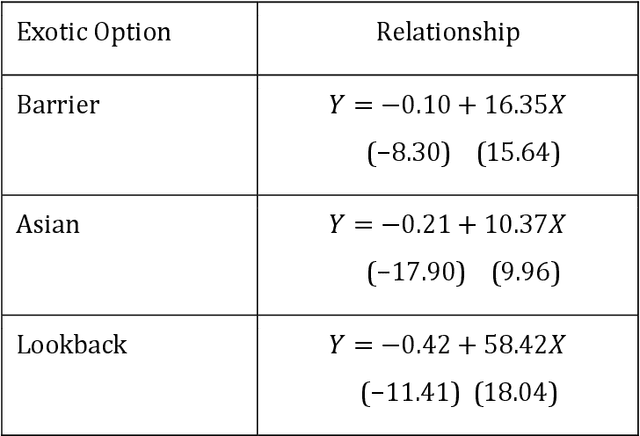
A common approach to valuing exotic options involves choosing a model and then determining its parameters to fit the volatility surface as closely as possible. We refer to this as the model calibration approach (MCA). This paper considers an alternative approach where the points on the volatility surface are features input to a neural network. We refer to this as the volatility feature approach (VFA). We conduct experiments showing that VFA can be expected to outperform MCA for the volatility surfaces encountered in practice. Once the upfront computational time has been invested in developing the neural network, the valuation of exotic options using VFA is very fast. VFA is a useful tool for the estimation of model risk. We illustrate this using S&P 500 data for the 2001 to 2019 period.