EX-DRL: Hedging Against Heavy Losses with EXtreme Distributional Reinforcement Learning

Recent advancements in Distributional Reinforcement Learning (DRL) for modeling loss distributions have shown promise in developing hedging strategies in derivatives markets. A common approach in DRL involves learning the quantiles of loss distributions at specified levels using Quantile Regression (QR). This method is particularly effective in option hedging due to its direct quantile-based risk assessment, such as Value at Risk (VaR) and Conditional Value at Risk (CVaR). However, these risk measures depend on the accurate estimation of extreme quantiles in the loss distribution's tail, which can be imprecise in QR-based DRL due to the rarity and extremity of tail data, as highlighted in the literature. To address this issue, we propose EXtreme DRL (EX-DRL), which enhances extreme quantile prediction by modeling the tail of the loss distribution with a Generalized Pareto Distribution (GPD). This method introduces supplementary data to mitigate the scarcity of extreme quantile observations, thereby improving estimation accuracy through QR. Comprehensive experiments on gamma hedging options demonstrate that EX-DRL improves existing QR-based models by providing more precise estimates of extreme quantiles, thereby improving the computation and reliability of risk metrics for complex financial risk management.

A Robust Quantile Huber Loss With Interpretable Parameter Adjustment In Distributional Reinforcement Learning

Distributional Reinforcement Learning (RL) estimates return distribution mainly by learning quantile values via minimizing the quantile Huber loss function, entailing a threshold parameter often selected heuristically or via hyperparameter search, which may not generalize well and can be suboptimal. This paper introduces a generalized quantile Huber loss function derived from Wasserstein distance (WD) calculation between Gaussian distributions, capturing noise in predicted (current) and target (Bellman-updated) quantile values. Compared to the classical quantile Huber loss, this innovative loss function enhances robustness against outliers. Notably, the classical Huber loss function can be seen as an approximation of our proposed loss, enabling parameter adjustment by approximating the amount of noise in the data during the learning process. Empirical tests on Atari games, a common application in distributional RL, and a recent hedging strategy using distributional RL, validate the effectiveness of our proposed loss function and its potential for parameter adjustments in distributional RL. The implementation of the proposed loss function is available here.

A unified uncertainty-aware exploration: Combining epistemic and aleatory uncertainty

Exploration is a significant challenge in practical reinforcement learning (RL), and uncertainty-aware exploration that incorporates the quantification of epistemic and aleatory uncertainty has been recognized as an effective exploration strategy. However, capturing the combined effect of aleatory and epistemic uncertainty for decision-making is difficult. Existing works estimate aleatory and epistemic uncertainty separately and consider the composite uncertainty as an additive combination of the two. Nevertheless, the additive formulation leads to excessive risk-taking behavior, causing instability. In this paper, we propose an algorithm that clarifies the theoretical connection between aleatory and epistemic uncertainty, unifies aleatory and epistemic uncertainty estimation, and quantifies the combined effect of both uncertainties for a risk-sensitive exploration. Our method builds on a novel extension of distributional RL that estimates a parameterized return distribution whose parameters are random variables encoding epistemic uncertainty. Experimental results on tasks with exploration and risk challenges show that our method outperforms alternative approaches.

Uncertainty-aware transfer across tasks using hybrid model-based successor feature reinforcement learning

Sample efficiency is central to developing practical reinforcement learning (RL) for complex and large-scale decision-making problems. The ability to transfer and generalize knowledge gained from previous experiences to downstream tasks can significantly improve sample efficiency. Recent research indicates that successor feature (SF) RL algorithms enable knowledge generalization between tasks with different rewards but identical transition dynamics. It has recently been hypothesized that combining model-based (MB) methods with SF algorithms can alleviate the limitation of fixed transition dynamics. Furthermore, uncertainty-aware exploration is widely recognized as another appealing approach for improving sample efficiency. Putting together two ideas of hybrid model-based successor feature (MB-SF) and uncertainty leads to an approach to the problem of sample efficient uncertainty-aware knowledge transfer across tasks with different transition dynamics or/and reward functions. In this paper, the uncertainty of the value of each action is approximated by a Kalman filter (KF)-based multiple-model adaptive estimation. This KF-based framework treats the parameters of a model as random variables. To the best of our knowledge, this is the first attempt at formulating a hybrid MB-SF algorithm capable of generalizing knowledge across large or continuous state space tasks with various transition dynamics while requiring less computation at decision time than MB methods. The number of samples required to learn the tasks was compared to recent SF and MB baselines. The results show that our algorithm generalizes its knowledge across different transition dynamics, learns downstream tasks with significantly fewer samples than starting from scratch, and outperforms existing approaches.

Combining information-seeking exploration and reward maximization: Unified inference on continuous state and action spaces under partial observability

Reinforcement learning (RL) gained considerable attention by creating decision-making agents that maximize rewards received from fully observable environments. However, many real-world problems are partially or noisily observable by nature, where agents do not receive the true and complete state of the environment. Such problems are formulated as partially observable Markov decision processes (POMDPs). Some studies applied RL to POMDPs by recalling previous decisions and observations or inferring the true state of the environment from received observations. Nevertheless, aggregating observations and decisions over time is impractical for environments with high-dimensional continuous state and action spaces. Moreover, so-called inference-based RL approaches require large number of samples to perform well since agents eschew uncertainty in the inferred state for the decision-making. Active inference is a framework that is naturally formulated in POMDPs and directs agents to select decisions by minimising expected free energy (EFE). This supplies reward-maximising (exploitative) behaviour in RL, with an information-seeking (exploratory) behaviour. Despite this exploratory behaviour of active inference, its usage is limited to discrete state and action spaces due to the computational difficulty of the EFE. We propose a unified principle for joint information-seeking and reward maximization that clarifies a theoretical connection between active inference and RL, unifies active inference and RL, and overcomes their aforementioned limitations. Our findings are supported by strong theoretical analysis. The proposed framework's superior exploration property is also validated by experimental results on partial observable tasks with high-dimensional continuous state and action spaces. Moreover, the results show that our model solves reward-free problems, making task reward design optional.

AKF-SR: Adaptive Kalman Filtering-based Successor Representation

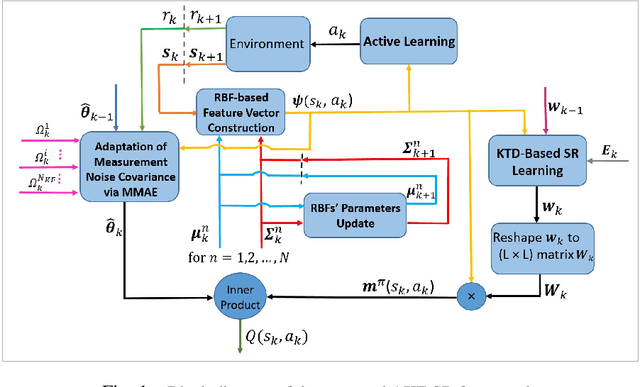
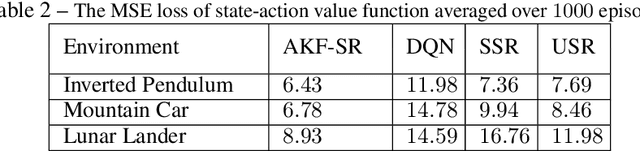
Recent studies in neuroscience suggest that Successor Representation (SR)-based models provide adaptation to changes in the goal locations or reward function faster than model-free algorithms, together with lower computational cost compared to that of model-based algorithms. However, it is not known how such representation might help animals to manage uncertainty in their decision-making. Existing methods for SR learning do not capture uncertainty about the estimated SR. In order to address this issue, the paper presents a Kalman filter-based SR framework, referred to as Adaptive Kalman Filtering-based Successor Representation (AKF-SR). First, Kalman temporal difference approach, which is a combination of the Kalman filter and the temporal difference method, is used within the AKF-SR framework to cast the SR learning procedure into a filtering problem to benefit from the uncertainty estimation of the SR, and also decreases in memory requirement and sensitivity to model's parameters in comparison to deep neural network-based algorithms. An adaptive Kalman filtering approach is then applied within the proposed AKF-SR framework in order to tune the measurement noise covariance and measurement mapping function of Kalman filter as the most important parameters affecting the filter's performance. Moreover, an active learning method that exploits the estimated uncertainty of the SR to form the behaviour policy leading to more visits to less certain values is proposed to improve the overall performance of an agent in terms of received rewards while interacting with its environment.

Multi-Agent Reinforcement Learning via Adaptive Kalman Temporal Difference and Successor Representation

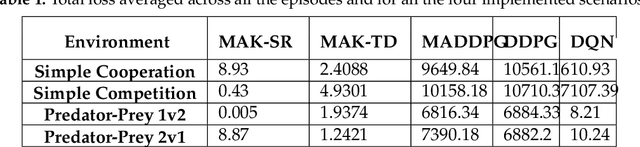
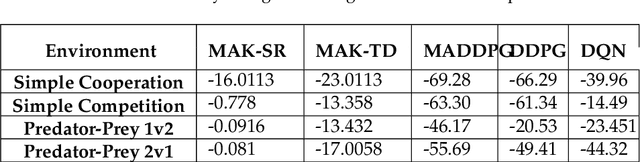
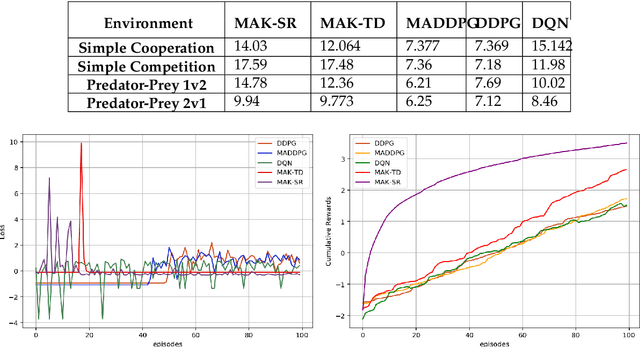
Distributed Multi-Agent Reinforcement Learning (MARL) algorithms has attracted a surge of interest lately mainly due to the recent advancements of Deep Neural Networks (DNNs). Conventional Model-Based (MB) or Model-Free (MF) RL algorithms are not directly applicable to the MARL problems due to utilization of a fixed reward model for learning the underlying value function. While DNN-based solutions perform utterly well when a single agent is involved, such methods fail to fully generalize to the complexities of MARL problems. In other words, although recently developed approaches based on DNNs for multi-agent environments have achieved superior performance, they are still prone to overfiting, high sensitivity to parameter selection, and sample inefficiency. The paper proposes the Multi-Agent Adaptive Kalman Temporal Difference (MAK-TD) framework and its Successor Representation-based variant, referred to as the MAK-SR. Intuitively speaking, the main objective is to capitalize on unique characteristics of Kalman Filtering (KF) such as uncertainty modeling and online second order learning. The proposed MAK-TD/SR frameworks consider the continuous nature of the action-space that is associated with high dimensional multi-agent environments and exploit Kalman Temporal Difference (KTD) to address the parameter uncertainty. By leveraging the KTD framework, SR learning procedure is modeled into a filtering problem, where Radial Basis Function (RBF) estimators are used to encode the continuous space into feature vectors. On the other hand, for learning localized reward functions, we resort to Multiple Model Adaptive Estimation (MMAE), to deal with the lack of prior knowledge on the observation noise covariance and observation mapping function. The proposed MAK-TD/SR frameworks are evaluated via several experiments, which are implemented through the OpenAI Gym MARL benchmarks.

MM-KTD: Multiple Model Kalman Temporal Differences for Reinforcement Learning

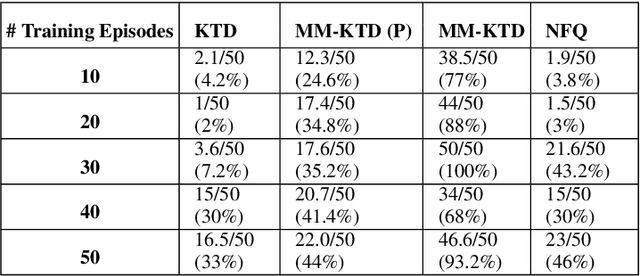
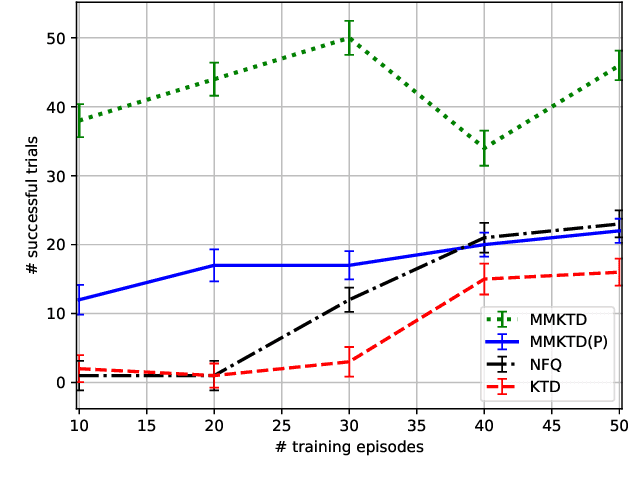
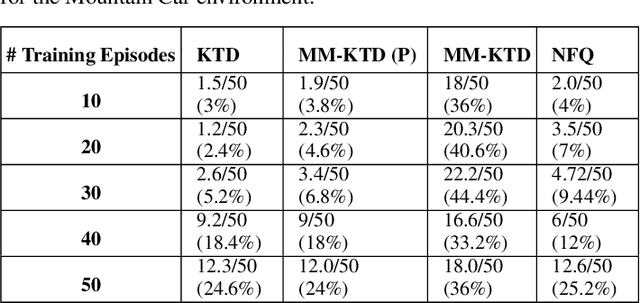
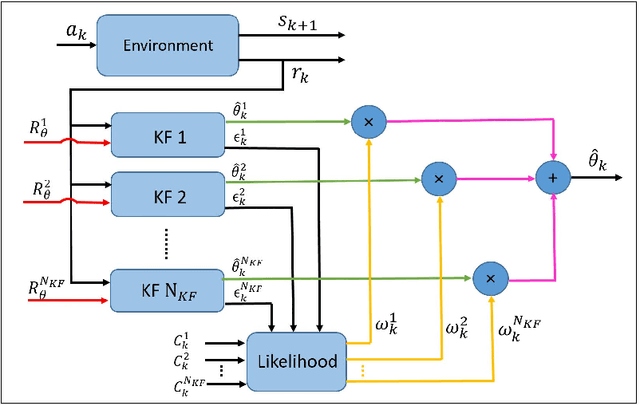
There has been an increasing surge of interest on development of advanced Reinforcement Learning (RL) systems as intelligent approaches to learn optimal control policies directly from smart agents' interactions with the environment. Objectives: In a model-free RL method with continuous state-space, typically, the value function of the states needs to be approximated. In this regard, Deep Neural Networks (DNNs) provide an attractive modeling mechanism to approximate the value function using sample transitions. DNN-based solutions, however, suffer from high sensitivity to parameter selection, are prone to overfitting, and are not very sample efficient. A Kalman-based methodology, on the other hand, could be used as an efficient alternative. Such an approach, however, commonly requires a-priori information about the system (such as noise statistics) to perform efficiently. The main objective of this paper is to address this issue. Methods: As a remedy to the aforementioned problems, this paper proposes an innovative Multiple Model Kalman Temporal Difference (MM-KTD) framework, which adapts the parameters of the filter using the observed states and rewards. Moreover, an active learning method is proposed to enhance the sampling efficiency of the system. More specifically, the estimated uncertainty of the value functions are exploited to form the behaviour policy leading to more visits to less certain values, therefore, improving the overall learning sample efficiency. As a result, the proposed MM-KTD framework can learn the optimal policy with significantly reduced number of samples as compared to its DNN-based counterparts. Results: To evaluate performance of the proposed MM-KTD framework, we have performed a comprehensive set of experiments based on three RL benchmarks. Experimental results show superiority of the MM-KTD framework in comparison to its state-of-the-art counterparts.