EX-DRL: Hedging Against Heavy Losses with EXtreme Distributional Reinforcement Learning

Recent advancements in Distributional Reinforcement Learning (DRL) for modeling loss distributions have shown promise in developing hedging strategies in derivatives markets. A common approach in DRL involves learning the quantiles of loss distributions at specified levels using Quantile Regression (QR). This method is particularly effective in option hedging due to its direct quantile-based risk assessment, such as Value at Risk (VaR) and Conditional Value at Risk (CVaR). However, these risk measures depend on the accurate estimation of extreme quantiles in the loss distribution's tail, which can be imprecise in QR-based DRL due to the rarity and extremity of tail data, as highlighted in the literature. To address this issue, we propose EXtreme DRL (EX-DRL), which enhances extreme quantile prediction by modeling the tail of the loss distribution with a Generalized Pareto Distribution (GPD). This method introduces supplementary data to mitigate the scarcity of extreme quantile observations, thereby improving estimation accuracy through QR. Comprehensive experiments on gamma hedging options demonstrate that EX-DRL improves existing QR-based models by providing more precise estimates of extreme quantiles, thereby improving the computation and reliability of risk metrics for complex financial risk management.

A Robust Quantile Huber Loss With Interpretable Parameter Adjustment In Distributional Reinforcement Learning

Distributional Reinforcement Learning (RL) estimates return distribution mainly by learning quantile values via minimizing the quantile Huber loss function, entailing a threshold parameter often selected heuristically or via hyperparameter search, which may not generalize well and can be suboptimal. This paper introduces a generalized quantile Huber loss function derived from Wasserstein distance (WD) calculation between Gaussian distributions, capturing noise in predicted (current) and target (Bellman-updated) quantile values. Compared to the classical quantile Huber loss, this innovative loss function enhances robustness against outliers. Notably, the classical Huber loss function can be seen as an approximation of our proposed loss, enabling parameter adjustment by approximating the amount of noise in the data during the learning process. Empirical tests on Atari games, a common application in distributional RL, and a recent hedging strategy using distributional RL, validate the effectiveness of our proposed loss function and its potential for parameter adjustments in distributional RL. The implementation of the proposed loss function is available here.

Deep Hedging of Derivatives Using Reinforcement Learning

This paper shows how reinforcement learning can be used to derive optimal hedging strategies for derivatives when there are transaction costs. The paper illustrates the approach by showing the difference between using delta hedging and optimal hedging for a short position in a call option when the objective is to minimize a function equal to the mean hedging cost plus a constant times the standard deviation of the hedging cost. Two situations are considered. In the first, the asset price follows a geometric Brownian motion. In the second, the asset price follows a stochastic volatility process. The paper extends the basic reinforcement learning approach in a number of ways. First, it uses two different Q-functions so that both the expected value of the cost and the expected value of the square of the cost are tracked for different state/action combinations. This approach increases the range of objective functions that can be used. Second, it uses a learning algorithm that allows for continuous state and action space. Third, it compares the accounting P&L approach (where the hedged position is valued at each step) and the cash flow approach (where cash inflows and outflows are used). We find that a hybrid approach involving the use of an accounting P&L approach that incorporates a relatively simple valuation model works well. The valuation model does not have to correspond to the process assumed for the underlying asset price.

Valuing Exotic Options and Estimating Model Risk

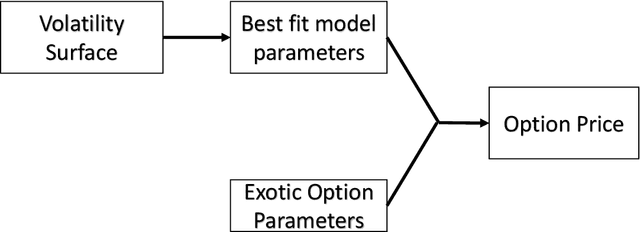
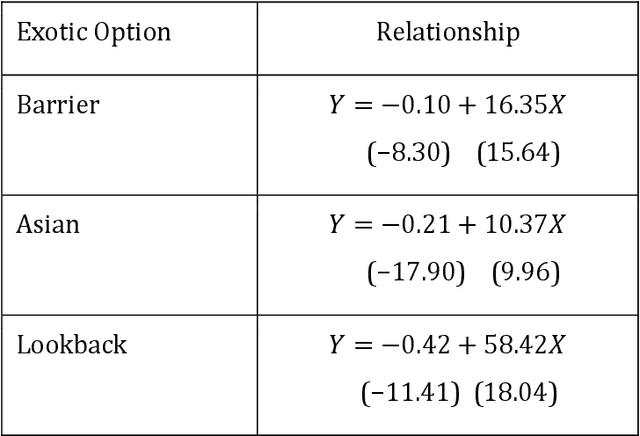
A common approach to valuing exotic options involves choosing a model and then determining its parameters to fit the volatility surface as closely as possible. We refer to this as the model calibration approach (MCA). This paper considers an alternative approach where the points on the volatility surface are features input to a neural network. We refer to this as the volatility feature approach (VFA). We conduct experiments showing that VFA can be expected to outperform MCA for the volatility surfaces encountered in practice. Once the upfront computational time has been invested in developing the neural network, the valuation of exotic options using VFA is very fast. VFA is a useful tool for the estimation of model risk. We illustrate this using S&P 500 data for the 2001 to 2019 period.

Training CNNs faster with Dynamic Input and Kernel Downsampling

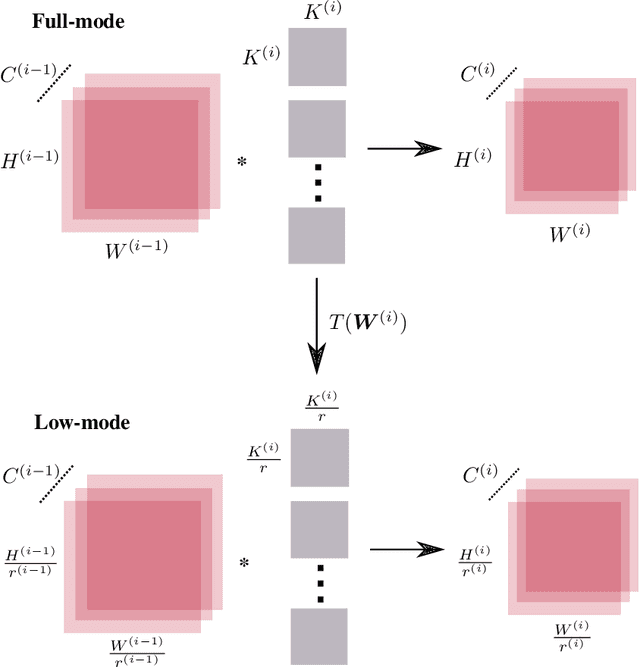
We reduce training time in convolutional networks (CNNs) with a method that, for some of the mini-batches: a) scales down the resolution of input images via downsampling, and b) reduces the forward pass operations via pooling on the convolution filters. Training is performed in an interleaved fashion; some batches undergo the regular forward and backpropagation passes with original network parameters, whereas others undergo a forward pass with pooled filters and downsampled inputs. Since pooling is differentiable, the gradients of the pooled filters propagate to the original network parameters for a standard parameter update. The latter phase requires fewer floating point operations and less storage due to the reduced spatial dimensions in feature maps and filters. The key idea is that this phase leads to smaller and approximate updates and thus slower learning, but at significantly reduced cost, followed by passes that use the original network parameters as a refinement stage. Deciding how often and for which batches the downsmapling occurs can be done either stochastically or deterministically, and can be defined as a training hyperparameter itself. Experiments on residual architectures show that we can achieve up to 23% reduction in training time with minimal loss in validation accuracy.

Bit-Tactical: Exploiting Ineffectual Computations in Convolutional Neural Networks: Which, Why, and How

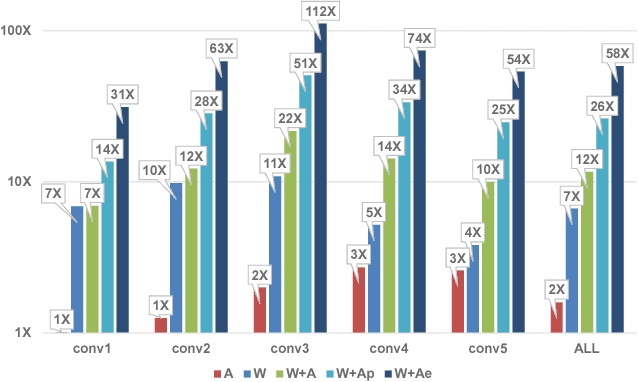
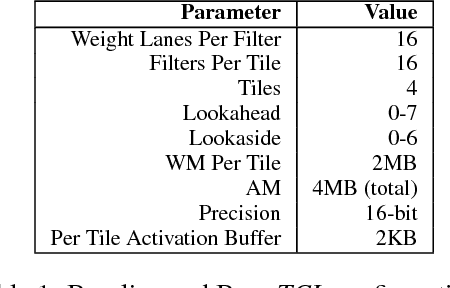
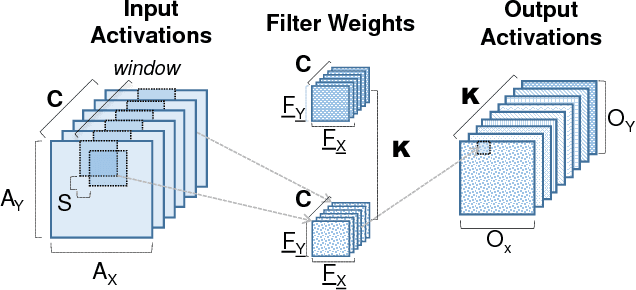
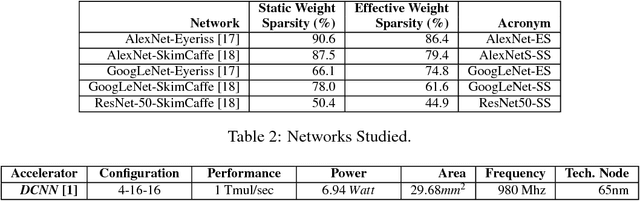
We show that, during inference with Convolutional Neural Networks (CNNs), more than 2x to $8x ineffectual work can be exposed if instead of targeting those weights and activations that are zero, we target different combinations of value stream properties. We demonstrate a practical application with Bit-Tactical (TCL), a hardware accelerator which exploits weight sparsity, per layer precision variability and dynamic fine-grain precision reduction for activations, and optionally the naturally occurring sparse effectual bit content of activations to improve performance and energy efficiency. TCL benefits both sparse and dense CNNs, natively supports both convolutional and fully-connected layers, and exploits properties of all activations to reduce storage, communication, and computation demands. While TCL does not require changes to the CNN to deliver benefits, it does reward any technique that would amplify any of the aforementioned weight and activation value properties. Compared to an equivalent data-parallel accelerator for dense CNNs, TCLp, a variant of TCL improves performance by 5.05x and is 2.98x more energy efficient while requiring 22% more area.