Implicit Bias of Gradient Descent for Non-Homogeneous Deep Networks

We establish the asymptotic implicit bias of gradient descent (GD) for generic non-homogeneous deep networks under exponential loss. Specifically, we characterize three key properties of GD iterates starting from a sufficiently small empirical risk, where the threshold is determined by a measure of the network's non-homogeneity. First, we show that a normalized margin induced by the GD iterates increases nearly monotonically. Second, we prove that while the norm of the GD iterates diverges to infinity, the iterates themselves converge in direction. Finally, we establish that this directional limit satisfies the Karush-Kuhn-Tucker (KKT) conditions of a margin maximization problem. Prior works on implicit bias have focused exclusively on homogeneous networks; in contrast, our results apply to a broad class of non-homogeneous networks satisfying a mild near-homogeneity condition. In particular, our results apply to networks with residual connections and non-homogeneous activation functions, thereby resolving an open problem posed by Ji and Telgarsky (2020).

Column and row subset selection using nuclear scores: algorithms and theory for Nyström approximation, CUR decomposition, and graph Laplacian reduction

Column selection is an essential tool for structure-preserving low-rank approximation, with wide-ranging applications across many fields, such as data science, machine learning, and theoretical chemistry. In this work, we develop unified methodologies for fast, efficient, and theoretically guaranteed column selection. First we derive and implement a sparsity-exploiting deterministic algorithm applicable to tasks including kernel approximation and CUR decomposition. Next, we develop a matrix-free formalism relying on a randomization scheme satisfying guaranteed concentration bounds, applying this construction both to CUR decomposition and to the approximation of matrix functions of graph Laplacians. Importantly, the randomization is only relevant for the computation of the scores that we use for column selection, not the selection itself given these scores. For both deterministic and matrix-free algorithms, we bound the performance favorably relative to the expected performance of determinantal point process (DPP) sampling and, in select scenarios, that of exactly optimal subset selection. The general case requires new analysis of the DPP expectation. Finally, we demonstrate strong real-world performance of our algorithms on a diverse set of example approximation tasks.

Large Stepsize Gradient Descent for Non-Homogeneous Two-Layer Networks: Margin Improvement and Fast Optimization

The typical training of neural networks using large stepsize gradient descent (GD) under the logistic loss often involves two distinct phases, where the empirical risk oscillates in the first phase but decreases monotonically in the second phase. We investigate this phenomenon in two-layer networks that satisfy a near-homogeneity condition. We show that the second phase begins once the empirical risk falls below a certain threshold, dependent on the stepsize. Additionally, we show that the normalized margin grows nearly monotonically in the second phase, demonstrating an implicit bias of GD in training non-homogeneous predictors. If the dataset is linearly separable and the derivative of the activation function is bounded away from zero, we show that the average empirical risk decreases, implying that the first phase must stop in finite steps. Finally, we demonstrate that by choosing a suitably large stepsize, GD that undergoes this phase transition is more efficient than GD that monotonically decreases the risk. Our analysis applies to networks of any width, beyond the well-known neural tangent kernel and mean-field regimes.

Multimarginal generative modeling with stochastic interpolants

Given a set of $K$ probability densities, we consider the multimarginal generative modeling problem of learning a joint distribution that recovers these densities as marginals. The structure of this joint distribution should identify multi-way correspondences among the prescribed marginals. We formalize an approach to this task within a generalization of the stochastic interpolant framework, leading to efficient learning algorithms built upon dynamical transport of measure. Our generative models are defined by velocity and score fields that can be characterized as the minimizers of simple quadratic objectives, and they are defined on a simplex that generalizes the time variable in the usual dynamical transport framework. The resulting transport on the simplex is influenced by all marginals, and we show that multi-way correspondences can be extracted. The identification of such correspondences has applications to style transfer, algorithmic fairness, and data decorruption. In addition, the multimarginal perspective enables an efficient algorithm for reducing the dynamical transport cost in the ordinary two-marginal setting. We demonstrate these capacities with several numerical examples.

Tensorizing flows: a tool for variational inference

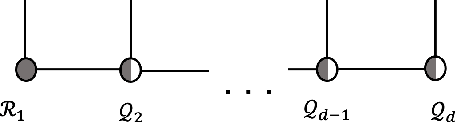
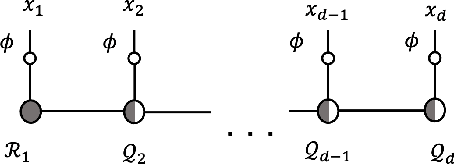
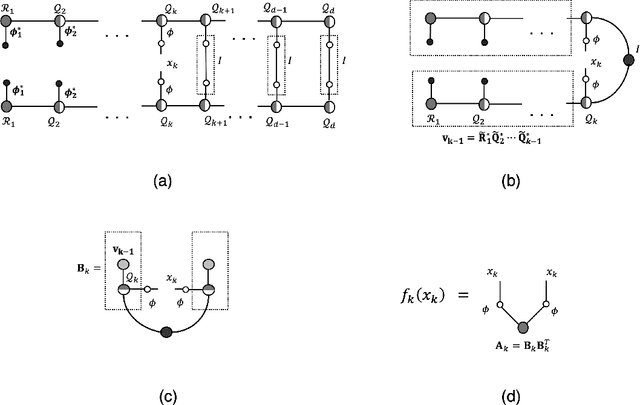
Fueled by the expressive power of deep neural networks, normalizing flows have achieved spectacular success in generative modeling, or learning to draw new samples from a distribution given a finite dataset of training samples. Normalizing flows have also been applied successfully to variational inference, wherein one attempts to learn a sampler based on an expression for the log-likelihood or energy function of the distribution, rather than on data. In variational inference, the unimodality of the reference Gaussian distribution used within the normalizing flow can cause difficulties in learning multimodal distributions. We introduce an extension of normalizing flows in which the Gaussian reference is replaced with a reference distribution that is constructed via a tensor network, specifically a matrix product state or tensor train. We show that by combining flows with tensor networks on difficult variational inference tasks, we can improve on the results obtained by using either tool without the other.

Understanding and eliminating spurious modes in variational Monte Carlo using collective variables

The use of neural network parametrizations to represent the ground state in variational Monte Carlo (VMC) calculations has generated intense interest in recent years. However, as we demonstrate in the context of the periodic Heisenberg spin chain, this approach can produce unreliable wave function approximations. One of the most obvious signs of failure is the occurrence of random, persistent spikes in the energy estimate during training. These energy spikes are caused by regions of configuration space that are over-represented by the wave function density, which are called ``spurious modes'' in the machine learning literature. After exploring these spurious modes in detail, we demonstrate that a collective-variable-based penalization yields a substantially more robust training procedure, preventing the formation of spurious modes and improving the accuracy of energy estimates. Because the penalization scheme is cheap to implement and is not specific to the particular model studied here, it can be extended to other applications of VMC where a reasonable choice of collective variable is available.

Rayleigh-Gauss-Newton optimization with enhanced sampling for variational Monte Carlo

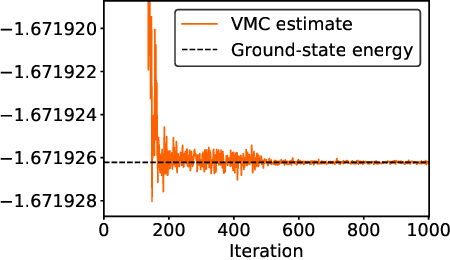
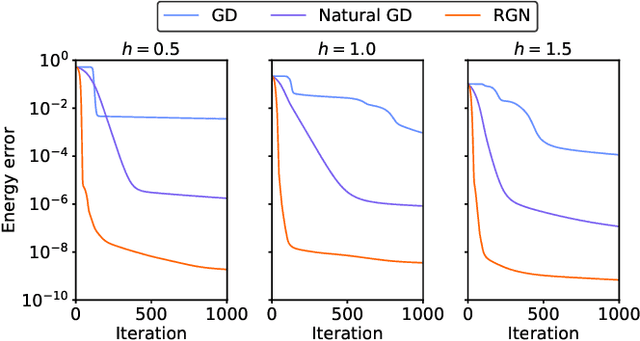
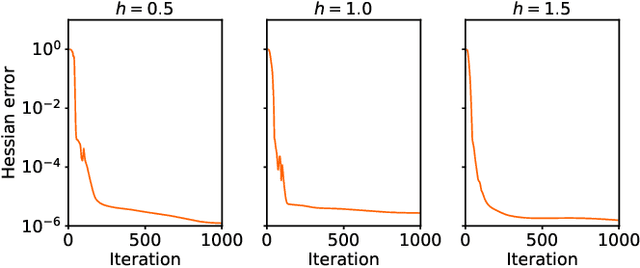
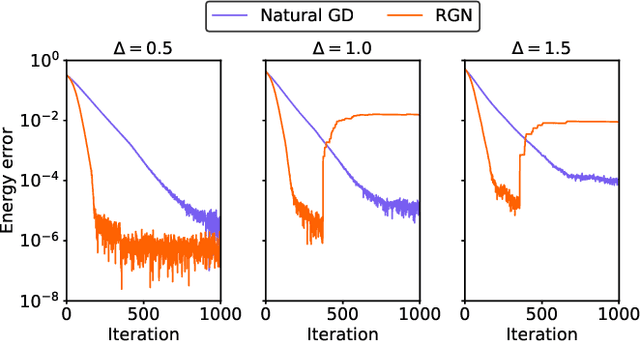
Variational Monte Carlo (VMC) is an approach for computing ground-state wavefunctions that has recently become more powerful due to the introduction of neural network-based wavefunction parametrizations. However, efficiently training neural wavefunctions to converge to an energy minimum remains a difficult problem. In this work, we analyze optimization and sampling methods used in VMC and introduce alterations to improve their performance. First, based on theoretical convergence analysis in a noiseless setting, we motivate a new optimizer that we call the Rayleigh-Gauss-Newton method, which can improve upon gradient descent and natural gradient descent to achieve superlinear convergence with little added computational cost. Second, in order to realize this favorable comparison in the presence of stochastic noise, we analyze the effect of sampling error on VMC parameter updates and experimentally demonstrate that it can be reduced by the parallel tempering method. In particular, we demonstrate that RGN can be made robust to energy spikes that occur when new regions of configuration space become available to the sampler over the course of optimization. Finally, putting theory into practice, we apply our enhanced optimization and sampling methods to the transverse-field Ising and XXZ models on large lattices, yielding ground-state energy estimates with remarkably high accuracy after just 200-500 parameter updates.