Benign Overfitting and the Geometry of the Ridge Regression Solution in Binary Classification

In this work, we investigate the behavior of ridge regression in an overparameterized binary classification task. We assume examples are drawn from (anisotropic) class-conditional cluster distributions with opposing means and we allow for the training labels to have a constant level of label-flipping noise. We characterize the classification error achieved by ridge regression under the assumption that the covariance matrix of the cluster distribution has a high effective rank in the tail. We show that ridge regression has qualitatively different behavior depending on the scale of the cluster mean vector and its interaction with the covariance matrix of the cluster distributions. In regimes where the scale is very large, the conditions that allow for benign overfitting turn out to be the same as those for the regression task. We additionally provide insights into how the introduction of label noise affects the behavior of the minimum norm interpolator (MNI). The optimal classifier in this setting is a linear transformation of the cluster mean vector and in the noiseless setting the MNI approximately learns this transformation. On the other hand, the introduction of label noise can significantly change the geometry of the solution while preserving the same qualitative behavior.

Implicit Bias of Gradient Descent for Non-Homogeneous Deep Networks

We establish the asymptotic implicit bias of gradient descent (GD) for generic non-homogeneous deep networks under exponential loss. Specifically, we characterize three key properties of GD iterates starting from a sufficiently small empirical risk, where the threshold is determined by a measure of the network's non-homogeneity. First, we show that a normalized margin induced by the GD iterates increases nearly monotonically. Second, we prove that while the norm of the GD iterates diverges to infinity, the iterates themselves converge in direction. Finally, we establish that this directional limit satisfies the Karush-Kuhn-Tucker (KKT) conditions of a margin maximization problem. Prior works on implicit bias have focused exclusively on homogeneous networks; in contrast, our results apply to a broad class of non-homogeneous networks satisfying a mild near-homogeneity condition. In particular, our results apply to networks with residual connections and non-homogeneous activation functions, thereby resolving an open problem posed by Ji and Telgarsky (2020).

A Statistical Analysis for Supervised Deep Learning with Exponential Families for Intrinsically Low-dimensional Data

Recent advances have revealed that the rate of convergence of the expected test error in deep supervised learning decays as a function of the intrinsic dimension and not the dimension $d$ of the input space. Existing literature defines this intrinsic dimension as the Minkowski dimension or the manifold dimension of the support of the underlying probability measures, which often results in sub-optimal rates and unrealistic assumptions. In this paper, we consider supervised deep learning when the response given the explanatory variable is distributed according to an exponential family with a $\beta$-H\"older smooth mean function. We consider an entropic notion of the intrinsic data-dimension and demonstrate that with $n$ independent and identically distributed samples, the test error scales as $\tilde{\mathcal{O}}\left(n^{-\frac{2\beta}{2\beta + \bar{d}_{2\beta}(\lambda)}}\right)$, where $\bar{d}_{2\beta}(\lambda)$ is the $2\beta$-entropic dimension of $\lambda$, the distribution of the explanatory variables. This improves on the best-known rates. Furthermore, under the assumption of an upper-bounded density of the explanatory variables, we characterize the rate of convergence as $\tilde{\mathcal{O}}\left( d^{\frac{2\lfloor\beta\rfloor(\beta + d)}{2\beta + d}}n^{-\frac{2\beta}{2\beta + d}}\right)$, establishing that the dependence on $d$ is not exponential but at most polynomial. We also demonstrate that when the explanatory variable has a lower bounded density, this rate in terms of the number of data samples, is nearly optimal for learning the dependence structure for exponential families.

A Statistical Analysis of Deep Federated Learning for Intrinsically Low-dimensional Data

Federated Learning (FL) has emerged as a groundbreaking paradigm in collaborative machine learning, emphasizing decentralized model training to address data privacy concerns. While significant progress has been made in optimizing federated learning, the exploration of generalization error, particularly in heterogeneous settings, has been limited, focusing mainly on parametric cases. This paper investigates the generalization properties of deep federated regression within a two-stage sampling model. Our findings highlight that the intrinsic dimension, defined by the entropic dimension, is crucial for determining convergence rates when appropriate network sizes are used. Specifically, if the true relationship between response and explanatory variables is charecterized by a $\beta$-H\"older function and there are $n$ independent and identically distributed (i.i.d.) samples from $m$ participating clients, the error rate for participating clients scales at most as $\tilde{O}\left((mn)^{-2\beta/(2\beta + \bar{d}_{2\beta}(\lambda))}\right)$, and for non-participating clients, it scales as $\tilde{O}\left(\Delta \cdot m^{-2\beta/(2\beta + \bar{d}_{2\beta}(\lambda))} + (mn)^{-2\beta/(2\beta + \bar{d}_{2\beta}(\lambda))}\right)$. Here, $\bar{d}_{2\beta}(\lambda)$ represents the $2\beta$-entropic dimension of $\lambda$, the marginal distribution of the explanatory variables, and $\Delta$ characterizes the dependence between the sampling stages. Our results explicitly account for the "closeness" of clients, demonstrating that the convergence rates of deep federated learners depend on intrinsic rather than nominal high-dimensionality.

Large Stepsize Gradient Descent for Non-Homogeneous Two-Layer Networks: Margin Improvement and Fast Optimization

The typical training of neural networks using large stepsize gradient descent (GD) under the logistic loss often involves two distinct phases, where the empirical risk oscillates in the first phase but decreases monotonically in the second phase. We investigate this phenomenon in two-layer networks that satisfy a near-homogeneity condition. We show that the second phase begins once the empirical risk falls below a certain threshold, dependent on the stepsize. Additionally, we show that the normalized margin grows nearly monotonically in the second phase, demonstrating an implicit bias of GD in training non-homogeneous predictors. If the dataset is linearly separable and the derivative of the activation function is bounded away from zero, we show that the average empirical risk decreases, implying that the first phase must stop in finite steps. Finally, we demonstrate that by choosing a suitably large stepsize, GD that undergoes this phase transition is more efficient than GD that monotonically decreases the risk. Our analysis applies to networks of any width, beyond the well-known neural tangent kernel and mean-field regimes.

Scaling Laws in Linear Regression: Compute, Parameters, and Data

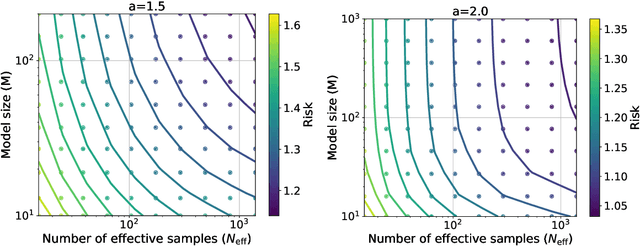
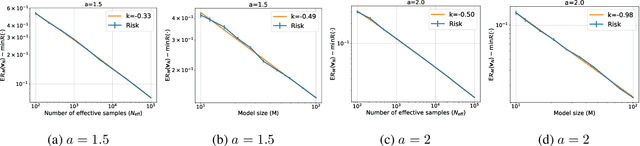
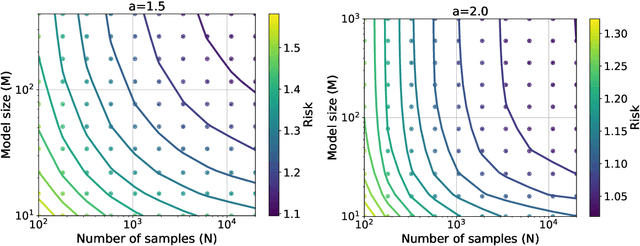
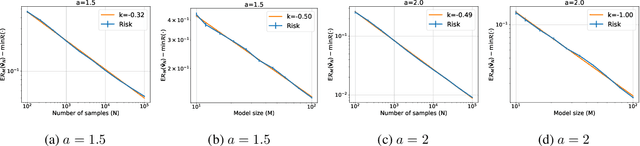
Empirically, large-scale deep learning models often satisfy a neural scaling law: the test error of the trained model improves polynomially as the model size and data size grow. However, conventional wisdom suggests the test error consists of approximation, bias, and variance errors, where the variance error increases with model size. This disagrees with the general form of neural scaling laws, which predict that increasing model size monotonically improves performance. We study the theory of scaling laws in an infinite dimensional linear regression setup. Specifically, we consider a model with $M$ parameters as a linear function of sketched covariates. The model is trained by one-pass stochastic gradient descent (SGD) using $N$ data. Assuming the optimal parameter satisfies a Gaussian prior and the data covariance matrix has a power-law spectrum of degree $a>1$, we show that the reducible part of the test error is $\Theta(M^{-(a-1)} + N^{-(a-1)/a})$. The variance error, which increases with $M$, is dominated by the other errors due to the implicit regularization of SGD, thus disappearing from the bound. Our theory is consistent with the empirical neural scaling laws and verified by numerical simulation.

Large Stepsize Gradient Descent for Logistic Loss: Non-Monotonicity of the Loss Improves Optimization Efficiency

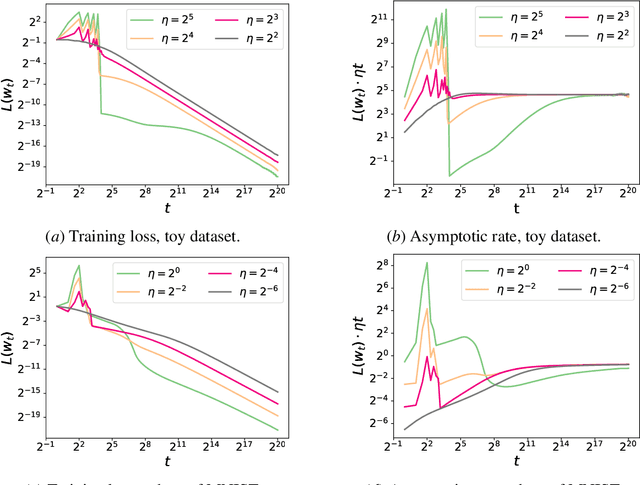
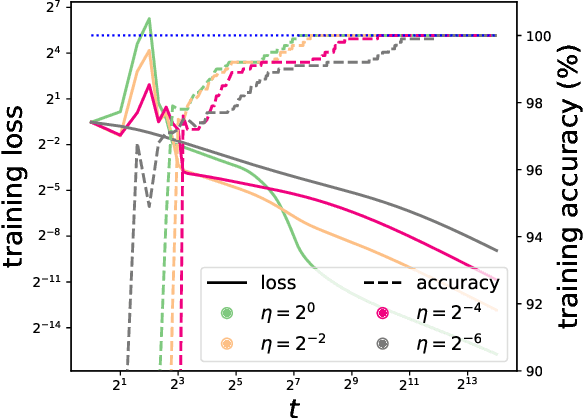
We consider gradient descent (GD) with a constant stepsize applied to logistic regression with linearly separable data, where the constant stepsize $\eta$ is so large that the loss initially oscillates. We show that GD exits this initial oscillatory phase rapidly -- in $\mathcal{O}(\eta)$ steps -- and subsequently achieves an $\tilde{\mathcal{O}}(1 / (\eta t) )$ convergence rate after $t$ additional steps. Our results imply that, given a budget of $T$ steps, GD can achieve an accelerated loss of $\tilde{\mathcal{O}}(1/T^2)$ with an aggressive stepsize $\eta:= \Theta( T)$, without any use of momentum or variable stepsize schedulers. Our proof technique is versatile and also handles general classification loss functions (where exponential tails are needed for the $\tilde{\mathcal{O}}(1/T^2)$ acceleration), nonlinear predictors in the neural tangent kernel regime, and online stochastic gradient descent (SGD) with a large stepsize, under suitable separability conditions.

A Statistical Analysis of Wasserstein Autoencoders for Intrinsically Low-dimensional Data

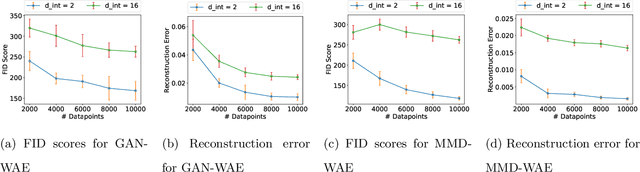
Variational Autoencoders (VAEs) have gained significant popularity among researchers as a powerful tool for understanding unknown distributions based on limited samples. This popularity stems partly from their impressive performance and partly from their ability to provide meaningful feature representations in the latent space. Wasserstein Autoencoders (WAEs), a variant of VAEs, aim to not only improve model efficiency but also interpretability. However, there has been limited focus on analyzing their statistical guarantees. The matter is further complicated by the fact that the data distributions to which WAEs are applied - such as natural images - are often presumed to possess an underlying low-dimensional structure within a high-dimensional feature space, which current theory does not adequately account for, rendering known bounds inefficient. To bridge the gap between the theory and practice of WAEs, in this paper, we show that WAEs can learn the data distributions when the network architectures are properly chosen. We show that the convergence rates of the expected excess risk in the number of samples for WAEs are independent of the high feature dimension, instead relying only on the intrinsic dimension of the data distribution.

In-Context Learning of a Linear Transformer Block: Benefits of the MLP Component and One-Step GD Initialization

We study the \emph{in-context learning} (ICL) ability of a \emph{Linear Transformer Block} (LTB) that combines a linear attention component and a linear multi-layer perceptron (MLP) component. For ICL of linear regression with a Gaussian prior and a \emph{non-zero mean}, we show that LTB can achieve nearly Bayes optimal ICL risk. In contrast, using only linear attention must incur an irreducible additive approximation error. Furthermore, we establish a correspondence between LTB and one-step gradient descent estimators with learnable initialization ($\mathsf{GD}\text{-}\mathbf{\beta}$), in the sense that every $\mathsf{GD}\text{-}\mathbf{\beta}$ estimator can be implemented by an LTB estimator and every optimal LTB estimator that minimizes the in-class ICL risk is effectively a $\mathsf{GD}\text{-}\mathbf{\beta}$ estimator. Finally, we show that $\mathsf{GD}\text{-}\mathbf{\beta}$ estimators can be efficiently optimized with gradient flow, despite a non-convex training objective. Our results reveal that LTB achieves ICL by implementing $\mathsf{GD}\text{-}\mathbf{\beta}$, and they highlight the role of MLP layers in reducing approximation error.

On the Statistical Properties of Generative Adversarial Models for Low Intrinsic Data Dimension

Despite the remarkable empirical successes of Generative Adversarial Networks (GANs), the theoretical guarantees for their statistical accuracy remain rather pessimistic. In particular, the data distributions on which GANs are applied, such as natural images, are often hypothesized to have an intrinsic low-dimensional structure in a typically high-dimensional feature space, but this is often not reflected in the derived rates in the state-of-the-art analyses. In this paper, we attempt to bridge the gap between the theory and practice of GANs and their bidirectional variant, Bi-directional GANs (BiGANs), by deriving statistical guarantees on the estimated densities in terms of the intrinsic dimension of the data and the latent space. We analytically show that if one has access to $n$ samples from the unknown target distribution and the network architectures are properly chosen, the expected Wasserstein-1 distance of the estimates from the target scales as $O\left( n^{-1/d_\mu } \right)$ for GANs and $O\left( n^{-1/(d_\mu+\ell)} \right)$ for BiGANs, where $d_\mu$ and $\ell$ are the upper Wasserstein-1 dimension of the data-distribution and latent-space dimension, respectively. The theoretical analyses not only suggest that these methods successfully avoid the curse of dimensionality, in the sense that the exponent of $n$ in the error rates does not depend on the data dimension but also serve to bridge the gap between the theoretical analyses of GANs and the known sharp rates from optimal transport literature. Additionally, we demonstrate that GANs can effectively achieve the minimax optimal rate even for non-smooth underlying distributions, with the use of larger generator networks.