Convex Clustering Redefined: Robust Learning with the Median of Means Estimator

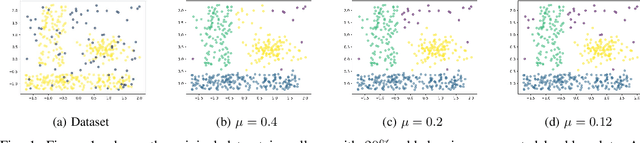
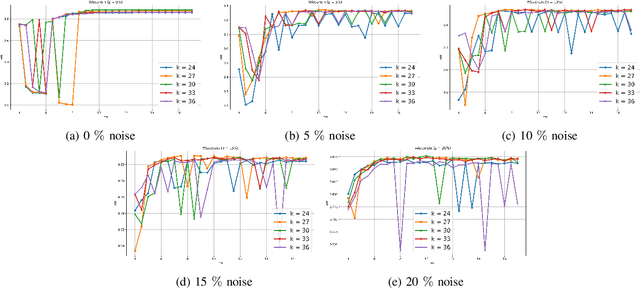
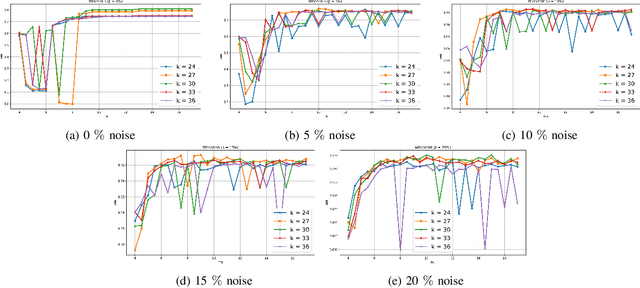
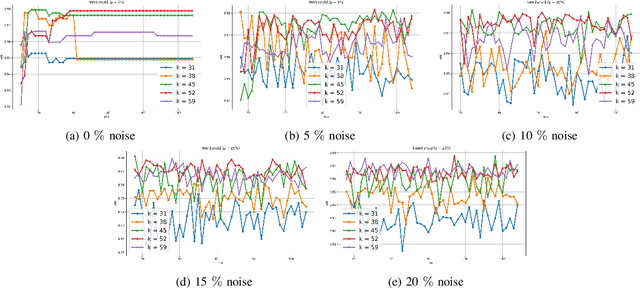
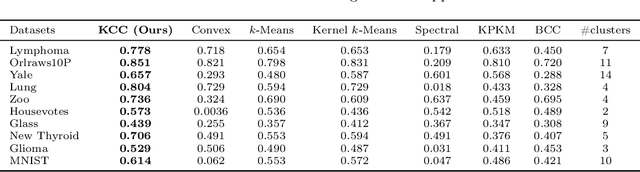
Clustering approaches that utilize convex loss functions have recently attracted growing interest in the formation of compact data clusters. Although classical methods like k-means and its wide family of variants are still widely used, all of them require the number of clusters k to be supplied as input, and many are notably sensitive to initialization. Convex clustering provides a more stable alternative by formulating the clustering task as a convex optimization problem, ensuring a unique global solution. However, it faces challenges in handling high-dimensional data, especially in the presence of noise and outliers. Additionally, strong fusion regularization, controlled by the tuning parameter, can hinder effective cluster formation within a convex clustering framework. To overcome these challenges, we introduce a robust approach that integrates convex clustering with the Median of Means (MoM) estimator, thus developing an outlier-resistant and efficient clustering framework that does not necessitate prior knowledge of the number of clusters. By leveraging the robustness of MoM alongside the stability of convex clustering, our method enhances both performance and efficiency, especially on large-scale datasets. Theoretical analysis demonstrates weak consistency under specific conditions, while experiments on synthetic and real-world datasets validate the method's superior performance compared to existing approaches.

A New Framework for Convex Clustering in Kernel Spaces: Finite Sample Bounds, Consistency and Performance Insights

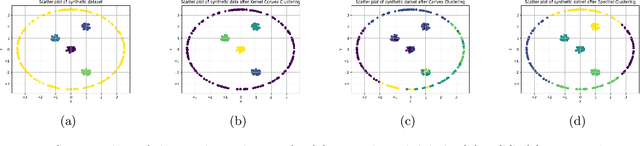
Convex clustering is a well-regarded clustering method, resembling the similar centroid-based approach of Lloyd's $k$-means, without requiring a predefined cluster count. It starts with each data point as its centroid and iteratively merges them. Despite its advantages, this method can fail when dealing with data exhibiting linearly non-separable or non-convex structures. To mitigate the limitations, we propose a kernelized extension of the convex clustering method. This approach projects the data points into a Reproducing Kernel Hilbert Space (RKHS) using a feature map, enabling convex clustering in this transformed space. This kernelization not only allows for better handling of complex data distributions but also produces an embedding in a finite-dimensional vector space. We provide a comprehensive theoretical underpinnings for our kernelized approach, proving algorithmic convergence and establishing finite sample bounds for our estimates. The effectiveness of our method is demonstrated through extensive experiments on both synthetic and real-world datasets, showing superior performance compared to state-of-the-art clustering techniques. This work marks a significant advancement in the field, offering an effective solution for clustering in non-linear and non-convex data scenarios.

A Statistical Analysis for Supervised Deep Learning with Exponential Families for Intrinsically Low-dimensional Data

Recent advances have revealed that the rate of convergence of the expected test error in deep supervised learning decays as a function of the intrinsic dimension and not the dimension $d$ of the input space. Existing literature defines this intrinsic dimension as the Minkowski dimension or the manifold dimension of the support of the underlying probability measures, which often results in sub-optimal rates and unrealistic assumptions. In this paper, we consider supervised deep learning when the response given the explanatory variable is distributed according to an exponential family with a $\beta$-H\"older smooth mean function. We consider an entropic notion of the intrinsic data-dimension and demonstrate that with $n$ independent and identically distributed samples, the test error scales as $\tilde{\mathcal{O}}\left(n^{-\frac{2\beta}{2\beta + \bar{d}_{2\beta}(\lambda)}}\right)$, where $\bar{d}_{2\beta}(\lambda)$ is the $2\beta$-entropic dimension of $\lambda$, the distribution of the explanatory variables. This improves on the best-known rates. Furthermore, under the assumption of an upper-bounded density of the explanatory variables, we characterize the rate of convergence as $\tilde{\mathcal{O}}\left( d^{\frac{2\lfloor\beta\rfloor(\beta + d)}{2\beta + d}}n^{-\frac{2\beta}{2\beta + d}}\right)$, establishing that the dependence on $d$ is not exponential but at most polynomial. We also demonstrate that when the explanatory variable has a lower bounded density, this rate in terms of the number of data samples, is nearly optimal for learning the dependence structure for exponential families.

A Statistical Analysis of Deep Federated Learning for Intrinsically Low-dimensional Data

Federated Learning (FL) has emerged as a groundbreaking paradigm in collaborative machine learning, emphasizing decentralized model training to address data privacy concerns. While significant progress has been made in optimizing federated learning, the exploration of generalization error, particularly in heterogeneous settings, has been limited, focusing mainly on parametric cases. This paper investigates the generalization properties of deep federated regression within a two-stage sampling model. Our findings highlight that the intrinsic dimension, defined by the entropic dimension, is crucial for determining convergence rates when appropriate network sizes are used. Specifically, if the true relationship between response and explanatory variables is charecterized by a $\beta$-H\"older function and there are $n$ independent and identically distributed (i.i.d.) samples from $m$ participating clients, the error rate for participating clients scales at most as $\tilde{O}\left((mn)^{-2\beta/(2\beta + \bar{d}_{2\beta}(\lambda))}\right)$, and for non-participating clients, it scales as $\tilde{O}\left(\Delta \cdot m^{-2\beta/(2\beta + \bar{d}_{2\beta}(\lambda))} + (mn)^{-2\beta/(2\beta + \bar{d}_{2\beta}(\lambda))}\right)$. Here, $\bar{d}_{2\beta}(\lambda)$ represents the $2\beta$-entropic dimension of $\lambda$, the marginal distribution of the explanatory variables, and $\Delta$ characterizes the dependence between the sampling stages. Our results explicitly account for the "closeness" of clients, demonstrating that the convergence rates of deep federated learners depend on intrinsic rather than nominal high-dimensionality.

Neural-g: A Deep Learning Framework for Mixing Density Estimation

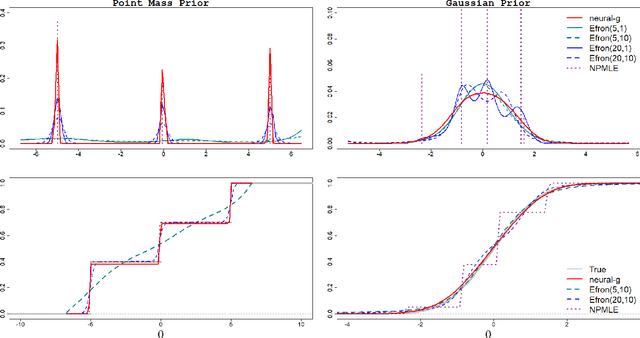
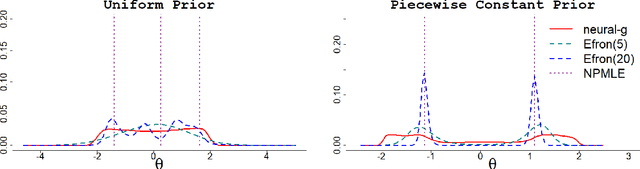
Mixing (or prior) density estimation is an important problem in machine learning and statistics, especially in empirical Bayes $g$-modeling where accurately estimating the prior is necessary for making good posterior inferences. In this paper, we propose neural-$g$, a new neural network-based estimator for $g$-modeling. Neural-$g$ uses a softmax output layer to ensure that the estimated prior is a valid probability density. Under default hyperparameters, we show that neural-$g$ is very flexible and capable of capturing many unknown densities, including those with flat regions, heavy tails, and/or discontinuities. In contrast, existing methods struggle to capture all of these prior shapes. We provide justification for neural-$g$ by establishing a new universal approximation theorem regarding the capability of neural networks to learn arbitrary probability mass functions. To accelerate convergence of our numerical implementation, we utilize a weighted average gradient descent approach to update the network parameters. Finally, we extend neural-$g$ to multivariate prior density estimation. We illustrate the efficacy of our approach through simulations and analyses of real datasets. A software package to implement neural-$g$ is publicly available at https://github.com/shijiew97/neuralG.

A Statistical Analysis of Wasserstein Autoencoders for Intrinsically Low-dimensional Data

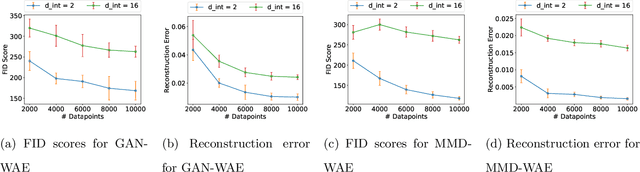
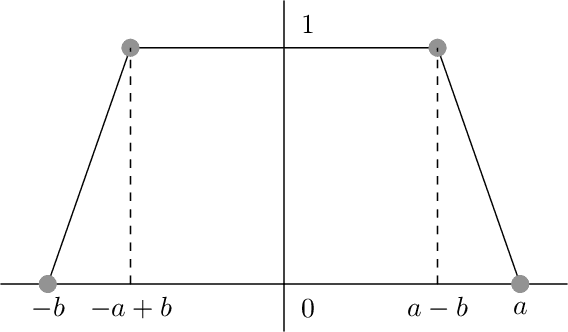
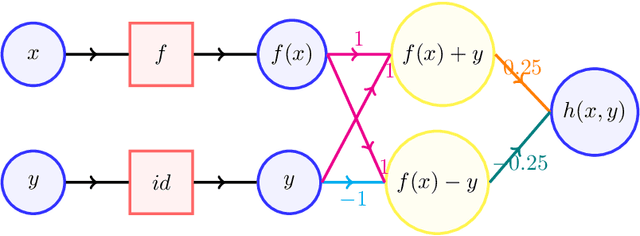
Variational Autoencoders (VAEs) have gained significant popularity among researchers as a powerful tool for understanding unknown distributions based on limited samples. This popularity stems partly from their impressive performance and partly from their ability to provide meaningful feature representations in the latent space. Wasserstein Autoencoders (WAEs), a variant of VAEs, aim to not only improve model efficiency but also interpretability. However, there has been limited focus on analyzing their statistical guarantees. The matter is further complicated by the fact that the data distributions to which WAEs are applied - such as natural images - are often presumed to possess an underlying low-dimensional structure within a high-dimensional feature space, which current theory does not adequately account for, rendering known bounds inefficient. To bridge the gap between the theory and practice of WAEs, in this paper, we show that WAEs can learn the data distributions when the network architectures are properly chosen. We show that the convergence rates of the expected excess risk in the number of samples for WAEs are independent of the high feature dimension, instead relying only on the intrinsic dimension of the data distribution.

On the Statistical Properties of Generative Adversarial Models for Low Intrinsic Data Dimension

Despite the remarkable empirical successes of Generative Adversarial Networks (GANs), the theoretical guarantees for their statistical accuracy remain rather pessimistic. In particular, the data distributions on which GANs are applied, such as natural images, are often hypothesized to have an intrinsic low-dimensional structure in a typically high-dimensional feature space, but this is often not reflected in the derived rates in the state-of-the-art analyses. In this paper, we attempt to bridge the gap between the theory and practice of GANs and their bidirectional variant, Bi-directional GANs (BiGANs), by deriving statistical guarantees on the estimated densities in terms of the intrinsic dimension of the data and the latent space. We analytically show that if one has access to $n$ samples from the unknown target distribution and the network architectures are properly chosen, the expected Wasserstein-1 distance of the estimates from the target scales as $O\left( n^{-1/d_\mu } \right)$ for GANs and $O\left( n^{-1/(d_\mu+\ell)} \right)$ for BiGANs, where $d_\mu$ and $\ell$ are the upper Wasserstein-1 dimension of the data-distribution and latent-space dimension, respectively. The theoretical analyses not only suggest that these methods successfully avoid the curse of dimensionality, in the sense that the exponent of $n$ in the error rates does not depend on the data dimension but also serve to bridge the gap between the theoretical analyses of GANs and the known sharp rates from optimal transport literature. Additionally, we demonstrate that GANs can effectively achieve the minimax optimal rate even for non-smooth underlying distributions, with the use of larger generator networks.

Bregman Power k-Means for Clustering Exponential Family Data

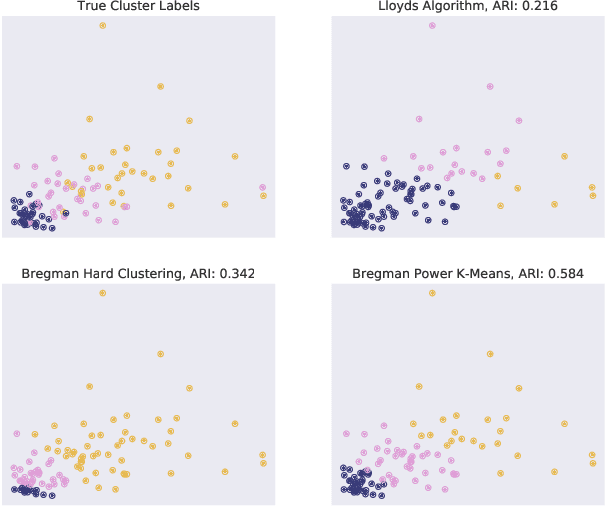
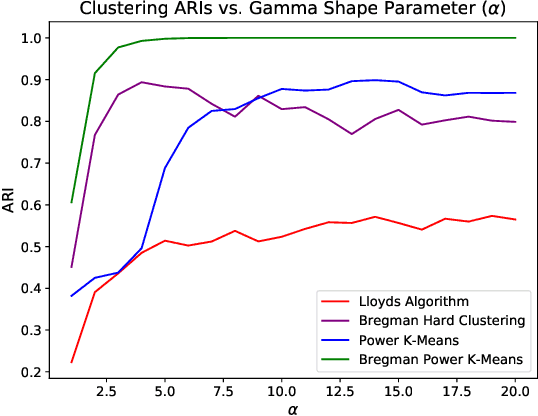
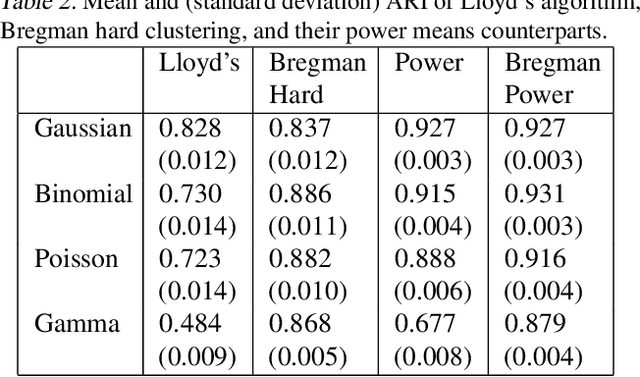
Recent progress in center-based clustering algorithms combats poor local minima by implicit annealing, using a family of generalized means. These methods are variations of Lloyd's celebrated $k$-means algorithm, and are most appropriate for spherical clusters such as those arising from Gaussian data. In this paper, we bridge these algorithmic advances to classical work on hard clustering under Bregman divergences, which enjoy a bijection to exponential family distributions and are thus well-suited for clustering objects arising from a breadth of data generating mechanisms. The elegant properties of Bregman divergences allow us to maintain closed form updates in a simple and transparent algorithm, and moreover lead to new theoretical arguments for establishing finite sample bounds that relax the bounded support assumption made in the existing state of the art. Additionally, we consider thorough empirical analyses on simulated experiments and a case study on rainfall data, finding that the proposed method outperforms existing peer methods in a variety of non-Gaussian data settings.

Robust Linear Predictions: Analyses of Uniform Concentration, Fast Rates and Model Misspecification

The problem of linear predictions has been extensively studied for the past century under pretty generalized frameworks. Recent advances in the robust statistics literature allow us to analyze robust versions of classical linear models through the prism of Median of Means (MoM). Combining these approaches in a piecemeal way might lead to ad-hoc procedures, and the restricted theoretical conclusions that underpin each individual contribution may no longer be valid. To meet these challenges coherently, in this study, we offer a unified robust framework that includes a broad variety of linear prediction problems on a Hilbert space, coupled with a generic class of loss functions. Notably, we do not require any assumptions on the distribution of the outlying data points ($\mathcal{O}$) nor the compactness of the support of the inlying ones ($\mathcal{I}$). Under mild conditions on the dual norm, we show that for misspecification level $\epsilon$, these estimators achieve an error rate of $O(\max\left\{|\mathcal{O}|^{1/2}n^{-1/2}, |\mathcal{I}|^{1/2}n^{-1} \right\}+\epsilon)$, matching the best-known rates in literature. This rate is slightly slower than the classical rates of $O(n^{-1/2})$, indicating that we need to pay a price in terms of error rates to obtain robust estimates. Additionally, we show that this rate can be improved to achieve so-called ``fast rates" under additional assumptions.

Uniform Concentration Bounds toward a Unified Framework for Robust Clustering

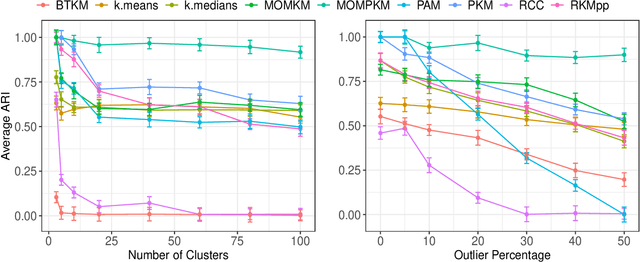
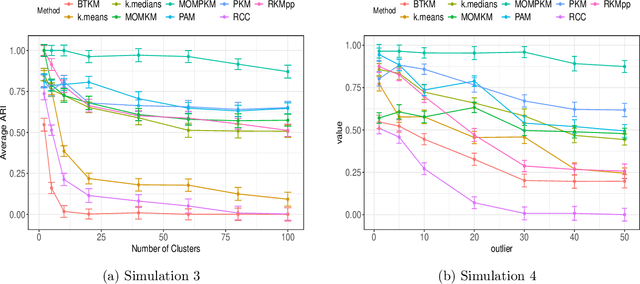
Recent advances in center-based clustering continue to improve upon the drawbacks of Lloyd's celebrated $k$-means algorithm over $60$ years after its introduction. Various methods seek to address poor local minima, sensitivity to outliers, and data that are not well-suited to Euclidean measures of fit, but many are supported largely empirically. Moreover, combining such approaches in a piecemeal manner can result in ad hoc methods, and the limited theoretical results supporting each individual contribution may no longer hold. Toward addressing these issues in a principled way, this paper proposes a cohesive robust framework for center-based clustering under a general class of dissimilarity measures. In particular, we present a rigorous theoretical treatment within a Median-of-Means (MoM) estimation framework, showing that it subsumes several popular $k$-means variants. In addition to unifying existing methods, we derive uniform concentration bounds that complete their analyses, and bridge these results to the MoM framework via Dudley's chaining arguments. Importantly, we neither require any assumptions on the distribution of the outlying observations nor on the relative number of observations $n$ to features $p$. We establish strong consistency and an error rate of $O(n^{-1/2})$ under mild conditions, surpassing the best-known results in the literature. The methods are empirically validated thoroughly on real and synthetic datasets.