Bayesian Transfer Learning

Transfer learning is a burgeoning concept in statistical machine learning that seeks to improve inference and/or predictive accuracy on a domain of interest by leveraging data from related domains. While the term "transfer learning" has garnered much recent interest, its foundational principles have existed for years under various guises. Prior literature reviews in computer science and electrical engineering have sought to bring these ideas into focus, primarily surveying general methodologies and works from these disciplines. This article highlights Bayesian approaches to transfer learning, which have received relatively limited attention despite their innate compatibility with the notion of drawing upon prior knowledge to guide new learning tasks. Our survey encompasses a wide range of Bayesian transfer learning frameworks applicable to a variety of practical settings. We discuss how these methods address the problem of finding the optimal information to transfer between domains, which is a central question in transfer learning. We illustrate the utility of Bayesian transfer learning methods via a simulation study where we compare performance against frequentist competitors.

Bregman Power k-Means for Clustering Exponential Family Data

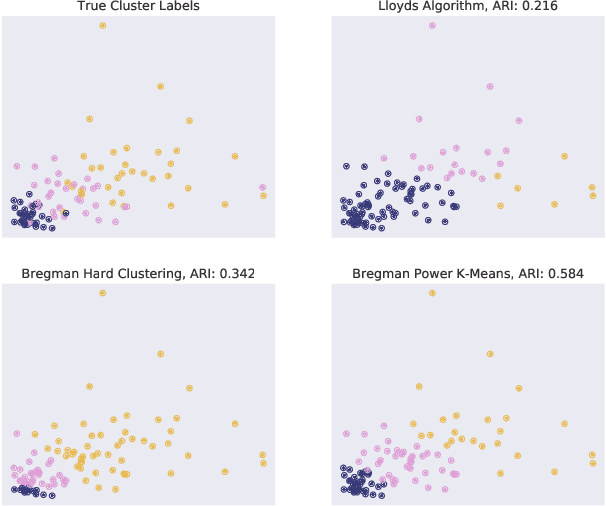
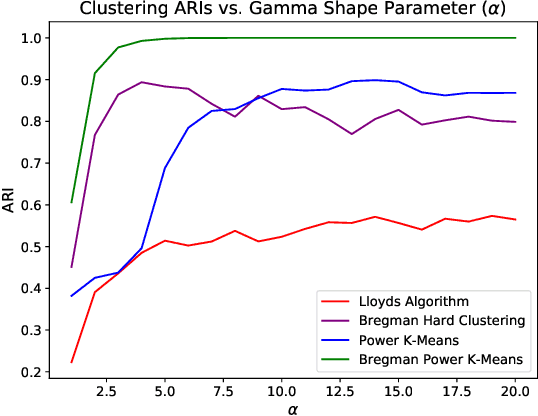
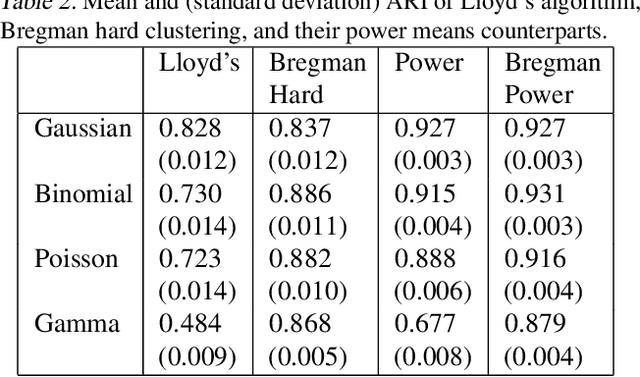
Recent progress in center-based clustering algorithms combats poor local minima by implicit annealing, using a family of generalized means. These methods are variations of Lloyd's celebrated $k$-means algorithm, and are most appropriate for spherical clusters such as those arising from Gaussian data. In this paper, we bridge these algorithmic advances to classical work on hard clustering under Bregman divergences, which enjoy a bijection to exponential family distributions and are thus well-suited for clustering objects arising from a breadth of data generating mechanisms. The elegant properties of Bregman divergences allow us to maintain closed form updates in a simple and transparent algorithm, and moreover lead to new theoretical arguments for establishing finite sample bounds that relax the bounded support assumption made in the existing state of the art. Additionally, we consider thorough empirical analyses on simulated experiments and a case study on rainfall data, finding that the proposed method outperforms existing peer methods in a variety of non-Gaussian data settings.

Wi-Fi and Bluetooth Contact Tracing Without User Intervention

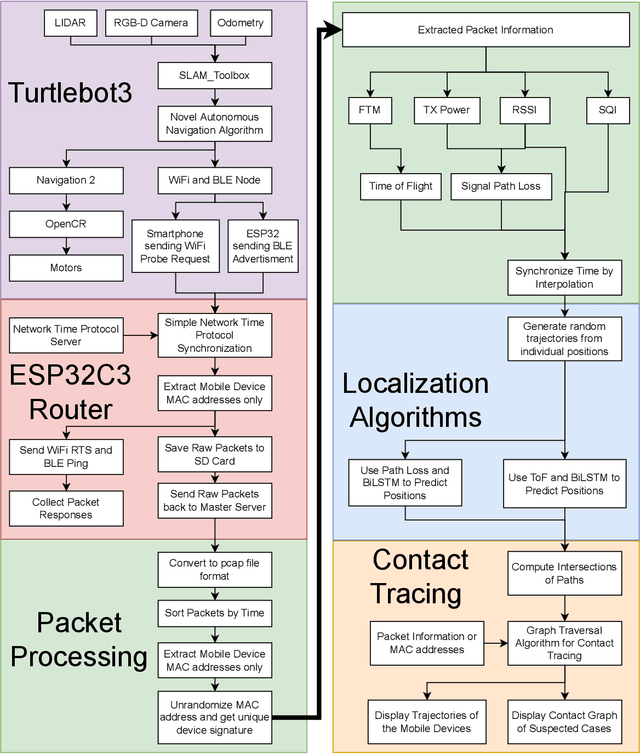
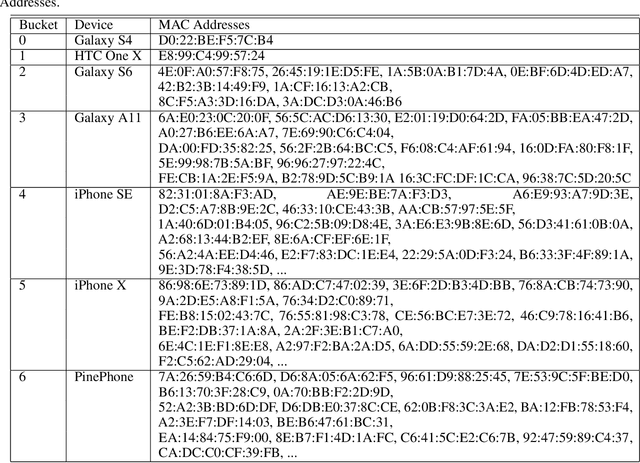
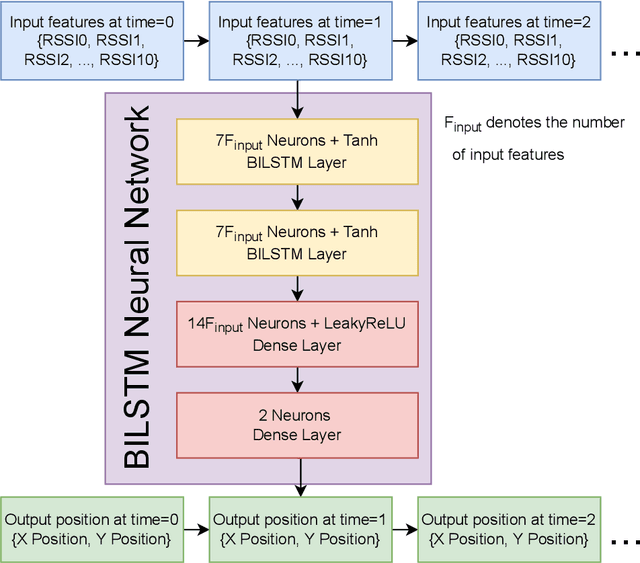
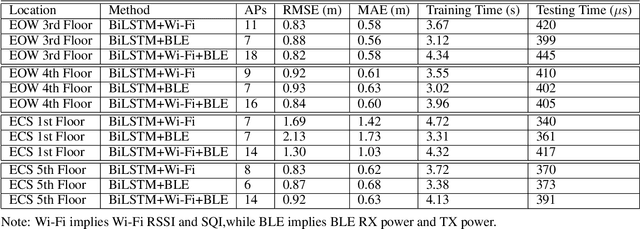
A custom Wi-Fi and Bluetooth indoor contact tracing system is created to find detailed paths of infected individuals without any user intervention. The system tracks smartphones, but it does not require smartphone applications, connecting to the routers, or any other extraneous devices on the users. A custom Turtlebot3 is used for site surveying, where it simulates mobile device movement and packet transmission. Transmit power, receive power, and round trip time are collected by a custom ESP32C3 router. MAC randomization is defeated to identify unique smartphones. Subsequently, the wireless parameters above are converted to signal path loss and time of flight. Bidirectional long short term memory takes the wireless parameters and predicts the detailed paths of the users within 1 m. Public health authorities can use the contact tracing website to find the detailed paths of the suspected cases using the smartphone models and initial positions of confirm cases. The system can also track indirect contact transmissions originating from surfaces and droplets due to having absolute positions of users.

Uniform Concentration Bounds toward a Unified Framework for Robust Clustering

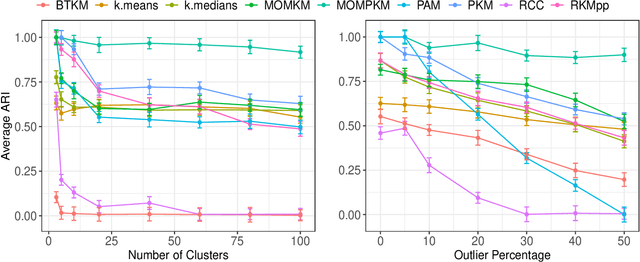
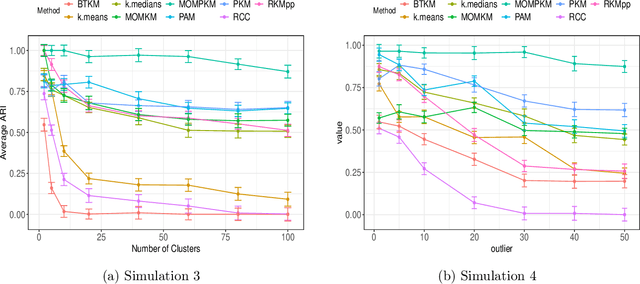
Recent advances in center-based clustering continue to improve upon the drawbacks of Lloyd's celebrated $k$-means algorithm over $60$ years after its introduction. Various methods seek to address poor local minima, sensitivity to outliers, and data that are not well-suited to Euclidean measures of fit, but many are supported largely empirically. Moreover, combining such approaches in a piecemeal manner can result in ad hoc methods, and the limited theoretical results supporting each individual contribution may no longer hold. Toward addressing these issues in a principled way, this paper proposes a cohesive robust framework for center-based clustering under a general class of dissimilarity measures. In particular, we present a rigorous theoretical treatment within a Median-of-Means (MoM) estimation framework, showing that it subsumes several popular $k$-means variants. In addition to unifying existing methods, we derive uniform concentration bounds that complete their analyses, and bridge these results to the MoM framework via Dudley's chaining arguments. Importantly, we neither require any assumptions on the distribution of the outlying observations nor on the relative number of observations $n$ to features $p$. We establish strong consistency and an error rate of $O(n^{-1/2})$ under mild conditions, surpassing the best-known results in the literature. The methods are empirically validated thoroughly on real and synthetic datasets.

Community Detection in Weighted Multilayer Networks with Ambient Noise

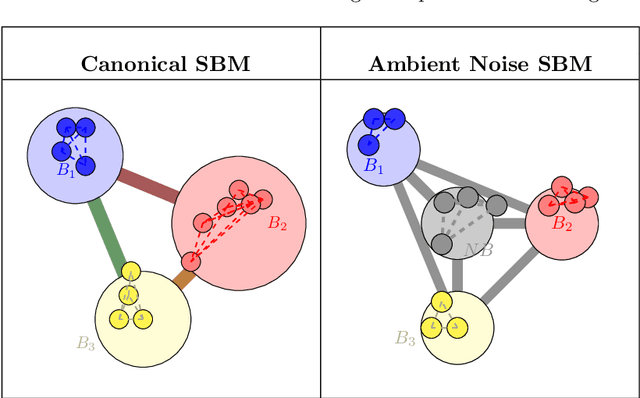
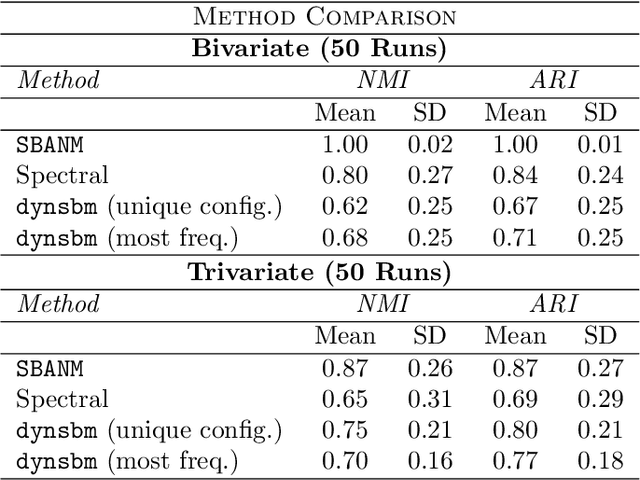
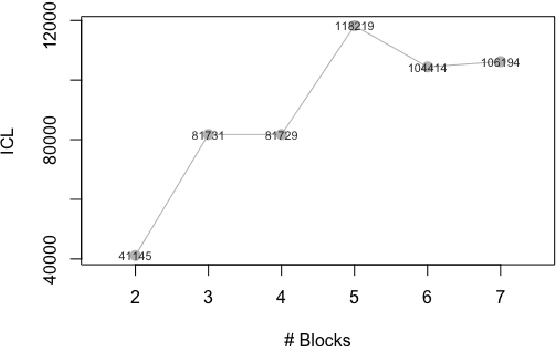
We introduce a novel class of stochastic blockmodel for multilayer weighted networks that accounts for the presence of a global ambient noise that governs between-block interactions. We induce a hierarchy of classifications in weighted multilayer networks by assuming that all but one cluster (block) are governed by unique local signals, while a single block is classified as ambient noise, which behaves identically as interactions across differing blocks. Hierarchical variational inference is employed to jointly detect and typologize block-structures as local signals or global noise. These principles are incorporated into novel community detection algorithm called Stochastic Block (with) Ambient Noise Model (SBANM) for multilayer weighted networks. We apply this method to several different domains. We focus on the Philadelphia Neurodevelopmental Cohort to discover communities of subjects that form diagnostic categories relating psychopathological symptoms to psychosis.

Kernel k-Means, By All Means: Algorithms and Strong Consistency

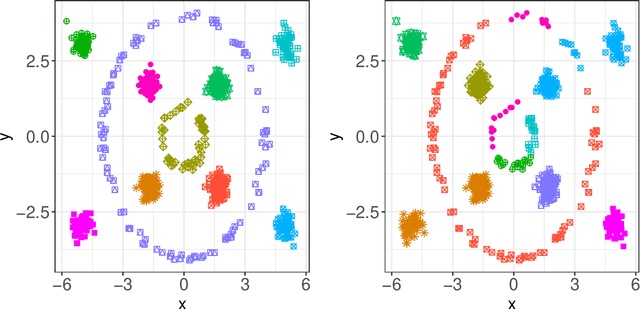
Kernel $k$-means clustering is a powerful tool for unsupervised learning of non-linearly separable data. Since the earliest attempts, researchers have noted that such algorithms often become trapped by local minima arising from non-convexity of the underlying objective function. In this paper, we generalize recent results leveraging a general family of means to combat sub-optimal local solutions to the kernel and multi-kernel settings. Called Kernel Power $k$-Means, our algorithm makes use of majorization-minimization (MM) to better solve this non-convex problem. We show the method implicitly performs annealing in kernel feature space while retaining efficient, closed-form updates, and we rigorously characterize its convergence properties both from computational and statistical points of view. In particular, we characterize the large sample behavior of the proposed method by establishing strong consistency guarantees. Its merits are thoroughly validated on a suite of simulated datasets and real data benchmarks that feature non-linear and multi-view separation.

A Scalable Framework for Sparse Clustering Without Shrinkage

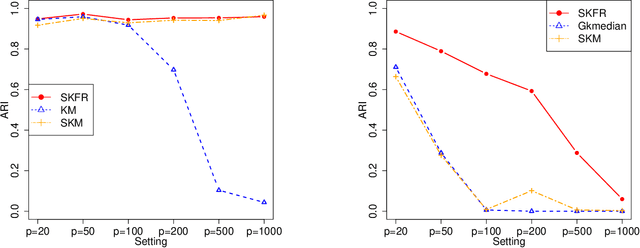
Clustering, a fundamental activity in unsupervised learning, is notoriously difficult when the feature space is high-dimensional. Fortunately, in many realistic scenarios, only a handful of features are relevant in distinguishing clusters. This has motivated the development of sparse clustering techniques that typically rely on k-means within outer algorithms of high computational complexity. Current techniques also require careful tuning of shrinkage parameters, further limiting their scalability. In this paper, we propose a novel framework for sparse k-means clustering that is intuitive, simple to implement, and competitive with state-of-the-art algorithms. We show that our algorithm enjoys consistency and convergence guarantees. Our core method readily generalizes to several task-specific algorithms such as clustering on subsets of attributes and in partially observed data settings. We showcase these contributions via simulated experiments and benchmark datasets, as well as a case study on mouse protein expression.

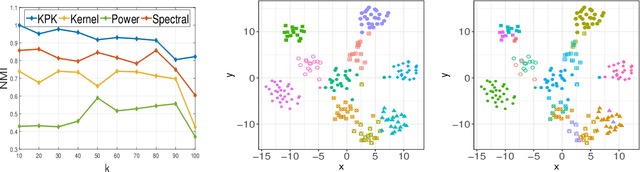
Entropy Regularized Power k-Means Clustering

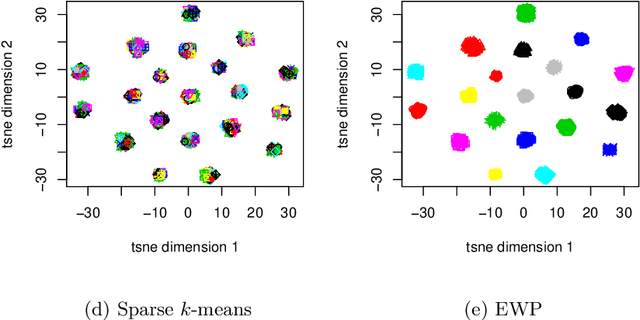
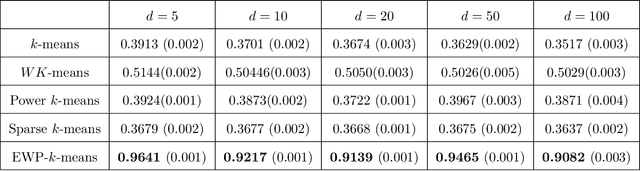
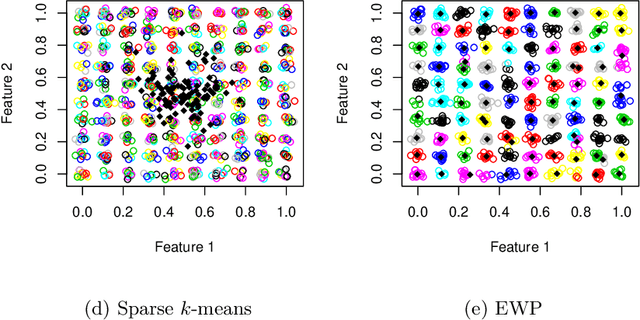
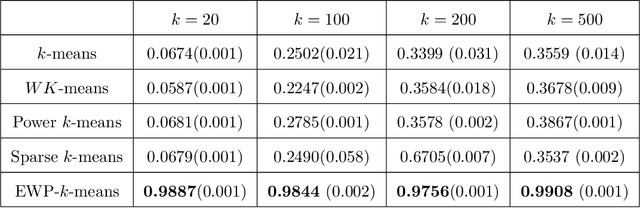
Despite its well-known shortcomings, $k$-means remains one of the most widely used approaches to data clustering. Current research continues to tackle its flaws while attempting to preserve its simplicity. Recently, the \textit{power $k$-means} algorithm was proposed to avoid trapping in local minima by annealing through a family of smoother surfaces. However, the approach lacks theoretical justification and fails in high dimensions when many features are irrelevant. This paper addresses these issues by introducing \textit{entropy regularization} to learn feature relevance while annealing. We prove consistency of the proposed approach and derive a scalable majorization-minimization algorithm that enjoys closed-form updates and convergence guarantees. In particular, our method retains the same computational complexity of $k$-means and power $k$-means, but yields significant improvements over both. Its merits are thoroughly assessed on a suite of real and synthetic data experiments.

Structural Risk Minimization for $C^{1,1}$ Regression

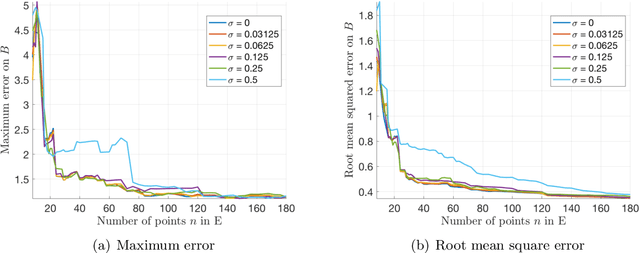
One means of fitting functions to high-dimensional data is by providing smoothness constraints. Recently, the following smooth function approximation problem was proposed: given a finite set $E \subset \mathbb{R}^d$ and a function $f: E \rightarrow \mathbb{R}$, interpolate the given information with a function $\widehat{f} \in \dot{C}^{1, 1}(\mathbb{R}^d)$ (the class of first-order differentiable functions with Lipschitz gradients) such that $\widehat{f}(a) = f(a)$ for all $a \in E$, and the value of $\mathrm{Lip}(\nabla \widehat{f})$ is minimal. An algorithm is provided that constructs such an approximating function $\widehat{f}$ and estimates the optimal Lipschitz constant $\mathrm{Lip}(\nabla \widehat{f})$ in the noiseless setting. We address statistical aspects of reconstructing the approximating function $\widehat{f}$ from a closely-related class $C^{1, 1}(\mathbb{R}^d)$ given samples from noisy data. We observe independent and identically distributed samples $y(a) = f(a) + \xi(a)$ for $a \in E$, where $\xi(a)$ is a noise term and the set $E \subset \mathbb{R}^d$ is fixed and known. We obtain uniform bounds relating the empirical risk and true risk over the class $\mathcal{F}_{\widetilde{M}} = \{f \in C^{1, 1}(\mathbb{R}^d) \mid \mathrm{Lip}(\nabla f) \leq \widetilde{M}\}$, where the quantity $\widetilde{M}$ grows with the number of samples at a rate governed by the metric entropy of the class $C^{1, 1}(\mathbb{R}^d)$. Finally, we provide an implementation using Vaidya's algorithm, supporting our results via numerical experiments on simulated data.

Automatic Conflict Detection in Police Body-Worn Audio

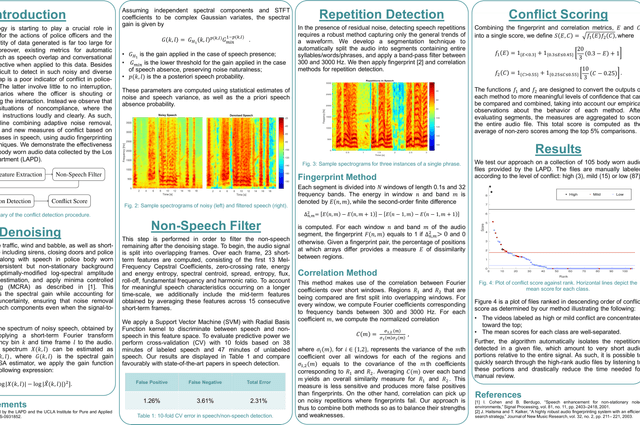
Automatic conflict detection has grown in relevance with the advent of body-worn technology, but existing metrics such as turn-taking and overlap are poor indicators of conflict in police-public interactions. Moreover, standard techniques to compute them fall short when applied to such diversified and noisy contexts. We develop a pipeline catered to this task combining adaptive noise removal, non-speech filtering and new measures of conflict based on the repetition and intensity of phrases in speech. We demonstrate the effectiveness of our approach on body-worn audio data collected by the Los Angeles Police Department.