Structural Risk Minimization for $C^{1,1}$ Regression

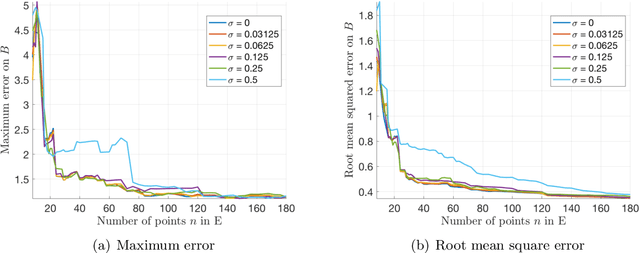
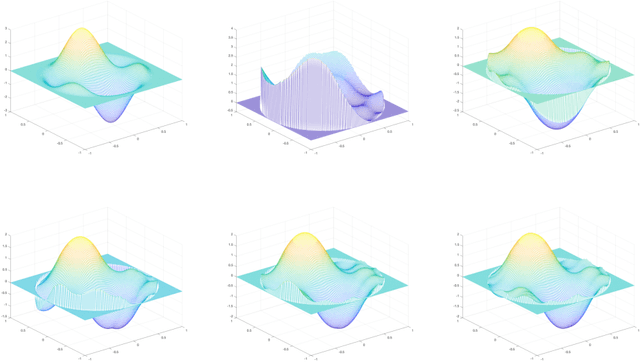
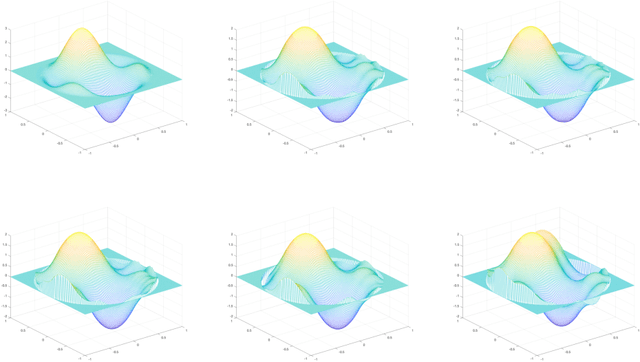
One means of fitting functions to high-dimensional data is by providing smoothness constraints. Recently, the following smooth function approximation problem was proposed: given a finite set $E \subset \mathbb{R}^d$ and a function $f: E \rightarrow \mathbb{R}$, interpolate the given information with a function $\widehat{f} \in \dot{C}^{1, 1}(\mathbb{R}^d)$ (the class of first-order differentiable functions with Lipschitz gradients) such that $\widehat{f}(a) = f(a)$ for all $a \in E$, and the value of $\mathrm{Lip}(\nabla \widehat{f})$ is minimal. An algorithm is provided that constructs such an approximating function $\widehat{f}$ and estimates the optimal Lipschitz constant $\mathrm{Lip}(\nabla \widehat{f})$ in the noiseless setting. We address statistical aspects of reconstructing the approximating function $\widehat{f}$ from a closely-related class $C^{1, 1}(\mathbb{R}^d)$ given samples from noisy data. We observe independent and identically distributed samples $y(a) = f(a) + \xi(a)$ for $a \in E$, where $\xi(a)$ is a noise term and the set $E \subset \mathbb{R}^d$ is fixed and known. We obtain uniform bounds relating the empirical risk and true risk over the class $\mathcal{F}_{\widetilde{M}} = \{f \in C^{1, 1}(\mathbb{R}^d) \mid \mathrm{Lip}(\nabla f) \leq \widetilde{M}\}$, where the quantity $\widetilde{M}$ grows with the number of samples at a rate governed by the metric entropy of the class $C^{1, 1}(\mathbb{R}^d)$. Finally, we provide an implementation using Vaidya's algorithm, supporting our results via numerical experiments on simulated data.

Manifold Learning Using Kernel Density Estimation and Local Principal Components Analysis

We consider the problem of recovering a $d-$dimensional manifold $\mathcal{M} \subset \mathbb{R}^n$ when provided with noiseless samples from $\mathcal{M}$. There are many algorithms (e.g., Isomap) that are used in practice to fit manifolds and thus reduce the dimensionality of a given data set. Ideally, the estimate $\mathcal{M}_\mathrm{put}$ of $\mathcal{M}$ should be an actual manifold of a certain smoothness; furthermore, $\mathcal{M}_\mathrm{put}$ should be arbitrarily close to $\mathcal{M}$ in Hausdorff distance given a large enough sample. Generally speaking, existing manifold learning algorithms do not meet these criteria. Fefferman, Mitter, and Narayanan (2016) have developed an algorithm whose output is provably a manifold. The key idea is to define an approximate squared-distance function (asdf) to $\mathcal{M}$. Then, $\mathcal{M}_\mathrm{put}$ is given by the set of points where the gradient of the asdf is orthogonal to the subspace spanned by the largest $n - d$ eigenvectors of the Hessian of the asdf. As long as the asdf meets certain regularity conditions, $\mathcal{M}_\mathrm{put}$ is a manifold that is arbitrarily close in Hausdorff distance to $\mathcal{M}$. In this paper, we define two asdfs that can be calculated from the data and show that they meet the required regularity conditions. The first asdf is based on kernel density estimation, and the second is based on estimation of tangent spaces using local principal components analysis.