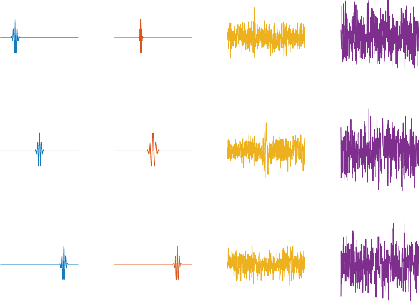
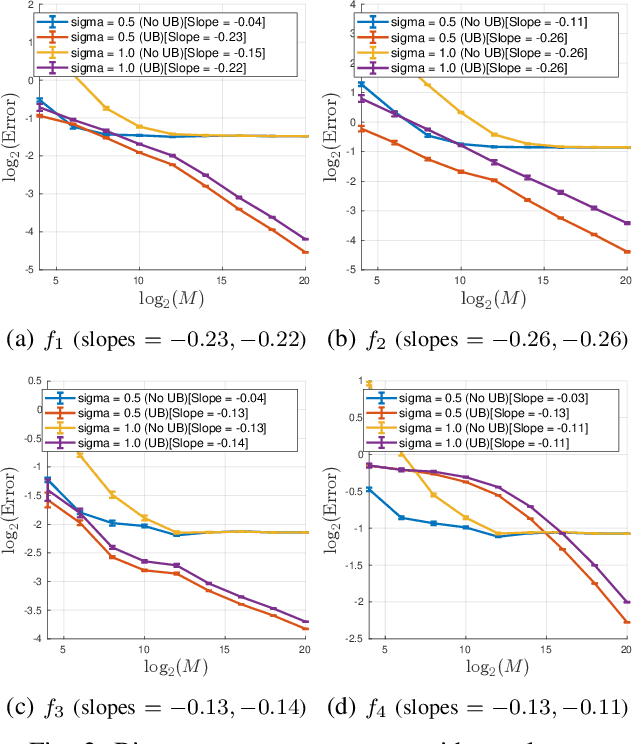
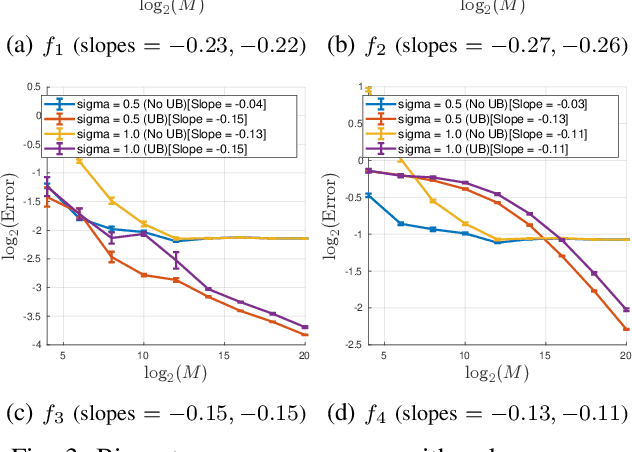
Bispectrum Unbiasing for Dilation-Invariant Multi-reference Alignment

Motivated by modern data applications such as cryo-electron microscopy, the goal of classic multi-reference alignment (MRA) is to recover an unknown signal $f: \mathbb{R} \to \mathbb{R}$ from many observations that have been randomly translated and corrupted by additive noise. We consider a generalization of classic MRA where signals are also corrupted by a random scale change, i.e. dilation. We propose a novel data-driven unbiasing procedure which can recover an unbiased estimator of the bispectrum of the unknown signal, given knowledge of the dilation distribution. Lastly, we invert the recovered bispectrum to achieve full signal recovery, and validate our methodology on a set of synthetic signals.

NervePool: A Simplicial Pooling Layer

For deep learning problems on graph-structured data, pooling layers are important for down sampling, reducing computational cost, and to minimize overfitting. We define a pooling layer, NervePool, for data structured as simplicial complexes, which are generalizations of graphs that include higher-dimensional simplices beyond vertices and edges; this structure allows for greater flexibility in modeling higher-order relationships. The proposed simplicial coarsening scheme is built upon partitions of vertices, which allow us to generate hierarchical representations of simplicial complexes, collapsing information in a learned fashion. NervePool builds on the learned vertex cluster assignments and extends to coarsening of higher dimensional simplices in a deterministic fashion. While in practice, the pooling operations are computed via a series of matrix operations, the topological motivation is a set-theoretic construction based on unions of stars of simplices and the nerve complex

Geometric Scattering on Measure Spaces

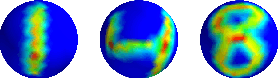
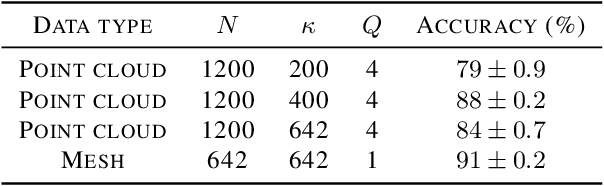
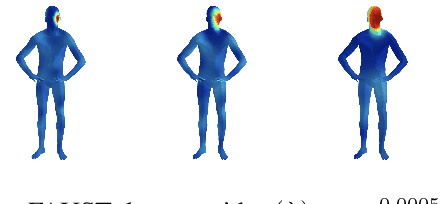
The scattering transform is a multilayered, wavelet-based transform initially introduced as a model of convolutional neural networks (CNNs) that has played a foundational role in our understanding of these networks' stability and invariance properties. Subsequently, there has been widespread interest in extending the success of CNNs to data sets with non-Euclidean structure, such as graphs and manifolds, leading to the emerging field of geometric deep learning. In order to improve our understanding of the architectures used in this new field, several papers have proposed generalizations of the scattering transform for non-Euclidean data structures such as undirected graphs and compact Riemannian manifolds without boundary. In this paper, we introduce a general, unified model for geometric scattering on measure spaces. Our proposed framework includes previous work on geometric scattering as special cases but also applies to more general settings such as directed graphs, signed graphs, and manifolds with boundary. We propose a new criterion that identifies to which groups a useful representation should be invariant and show that this criterion is sufficient to guarantee that the scattering transform has desirable stability and invariance properties. Additionally, we consider finite measure spaces that are obtained from randomly sampling an unknown manifold. We propose two methods for constructing a data-driven graph on which the associated graph scattering transform approximates the scattering transform on the underlying manifold. Moreover, we use a diffusion-maps based approach to prove quantitative estimates on the rate of convergence of one of these approximations as the number of sample points tends to infinity. Lastly, we showcase the utility of our method on spherical images, directed graphs, and on high-dimensional single-cell data.

The Manifold Scattering Transform for High-Dimensional Point Cloud Data

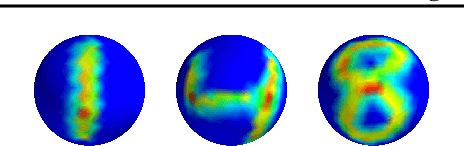
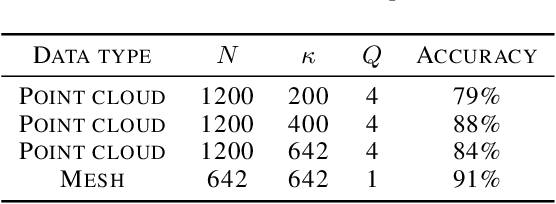
The manifold scattering transform is a deep feature extractor for data defined on a Riemannian manifold. It is one of the first examples of extending convolutional neural network-like operators to general manifolds. The initial work on this model focused primarily on its theoretical stability and invariance properties but did not provide methods for its numerical implementation except in the case of two-dimensional surfaces with predefined meshes. In this work, we present practical schemes, based on the theory of diffusion maps, for implementing the manifold scattering transform to datasets arising in naturalistic systems, such as single cell genetics, where the data is a high-dimensional point cloud modeled as lying on a low-dimensional manifold. We show that our methods are effective for signal classification and manifold classification tasks.

Taxonomy of Benchmarks in Graph Representation Learning

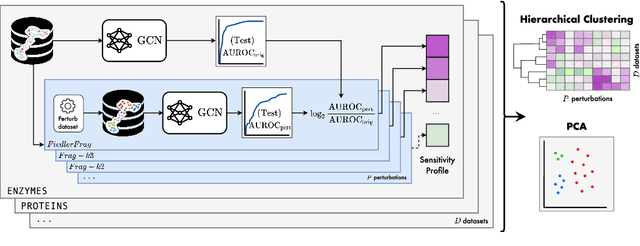
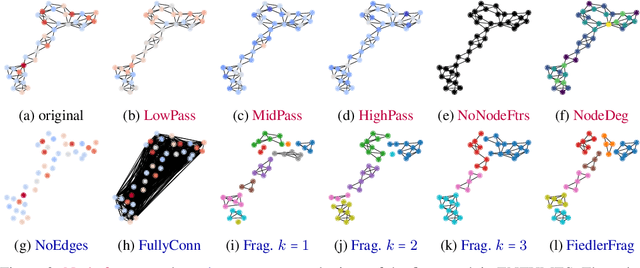
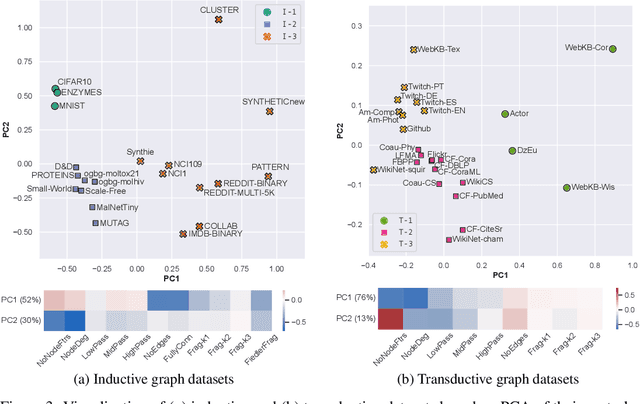
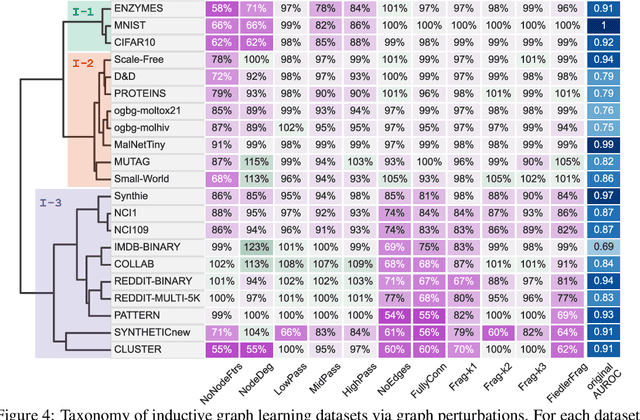
Graph Neural Networks (GNNs) extend the success of neural networks to graph-structured data by accounting for their intrinsic geometry. While extensive research has been done on developing GNN models with superior performance according to a collection of graph representation learning benchmarks, it is currently not well understood what aspects of a given model are probed by them. For example, to what extent do they test the ability of a model to leverage graph structure vs. node features? Here, we develop a principled approach to taxonomize benchmarking datasets according to a $\textit{sensitivity profile}$ that is based on how much GNN performance changes due to a collection of graph perturbations. Our data-driven analysis provides a deeper understanding of which benchmarking data characteristics are leveraged by GNNs. Consequently, our taxonomy can aid in selection and development of adequate graph benchmarks, and better informed evaluation of future GNN methods. Finally, our approach and implementation in $\texttt{GTaxoGym}$ package are extendable to multiple graph prediction task types and future datasets.

Time-inhomogeneous diffusion geometry and topology

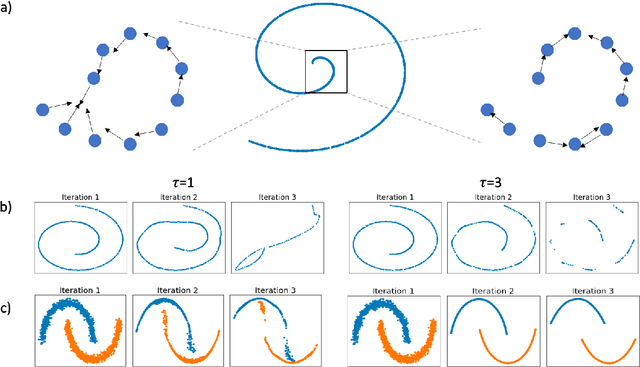
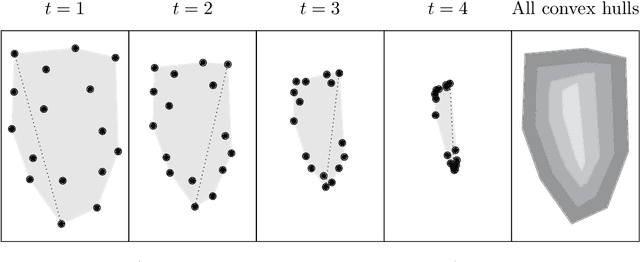
Diffusion condensation is a dynamic process that yields a sequence of multiscale data representations that aim to encode meaningful abstractions. It has proven effective for manifold learning, denoising, clustering, and visualization of high-dimensional data. Diffusion condensation is constructed as a time-inhomogeneous process where each step first computes and then applies a diffusion operator to the data. We theoretically analyze the convergence and evolution of this process from geometric, spectral, and topological perspectives. From a geometric perspective, we obtain convergence bounds based on the smallest transition probability and the radius of the data, whereas from a spectral perspective, our bounds are based on the eigenspectrum of the diffusion kernel. Our spectral results are of particular interest since most of the literature on data diffusion is focused on homogeneous processes. From a topological perspective, we show diffusion condensation generalizes centroid-based hierarchical clustering. We use this perspective to obtain a bound based on the number of data points, independent of their location. To understand the evolution of the data geometry beyond convergence, we use topological data analysis. We show that the condensation process itself defines an intrinsic diffusion homology. We use this intrinsic topology as well as an ambient topology to study how the data changes over diffusion time. We demonstrate both homologies in well-understood toy examples. Our work gives theoretical insights into the convergence of diffusion condensation, and shows that it provides a link between topological and geometric data analysis.

Overcoming Oversmoothness in Graph Convolutional Networks via Hybrid Scattering Networks

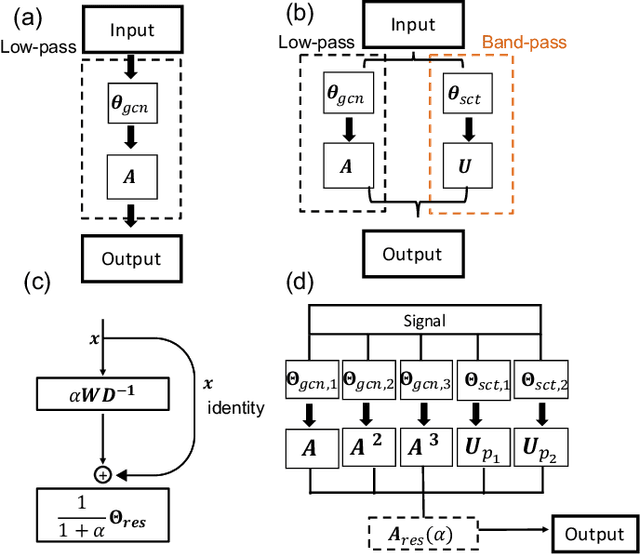
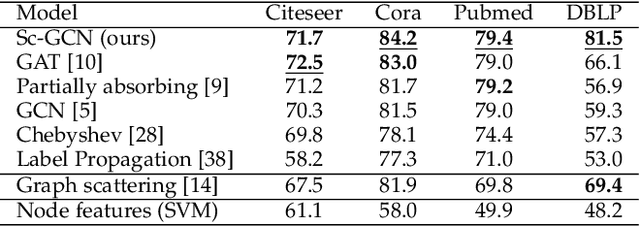
Geometric deep learning (GDL) has made great strides towards generalizing the design of structure-aware neural network architectures from traditional domains to non-Euclidean ones, such as graphs. This gave rise to graph neural network (GNN) models that can be applied to graph-structured datasets arising, for example, in social networks, biochemistry, and material science. Graph convolutional networks (GCNs) in particular, inspired by their Euclidean counterparts, have been successful in processing graph data by extracting structure-aware features. However, current GNN models (and GCNs in particular) are known to be constrained by various phenomena that limit their expressive power and ability to generalize to more complex graph datasets. Most models essentially rely on low-pass filtering of graph signals via local averaging operations, thus leading to oversmoothing. Here, we propose a hybrid GNN framework that combines traditional GCN filters with band-pass filters defined via the geometric scattering transform. We further introduce an attention framework that allows the model to locally attend over the combined information from different GNN filters at the node level. Our theoretical results establish the complementary benefits of the scattering filters to leverage structural information from the graph, while our experiments show the benefits of our method on various learning tasks.

Towards a Taxonomy of Graph Learning Datasets

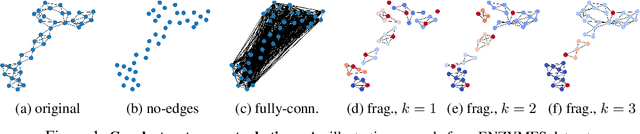
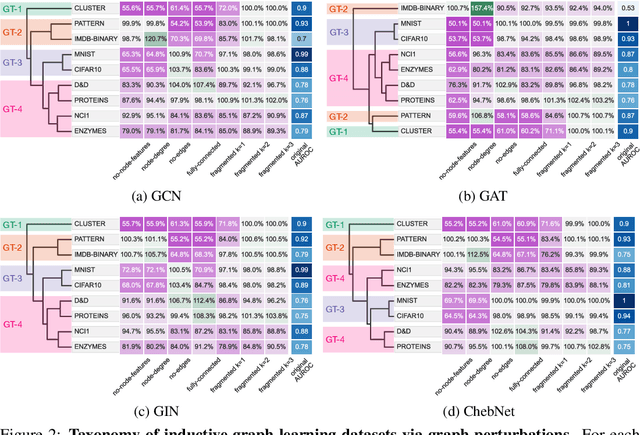
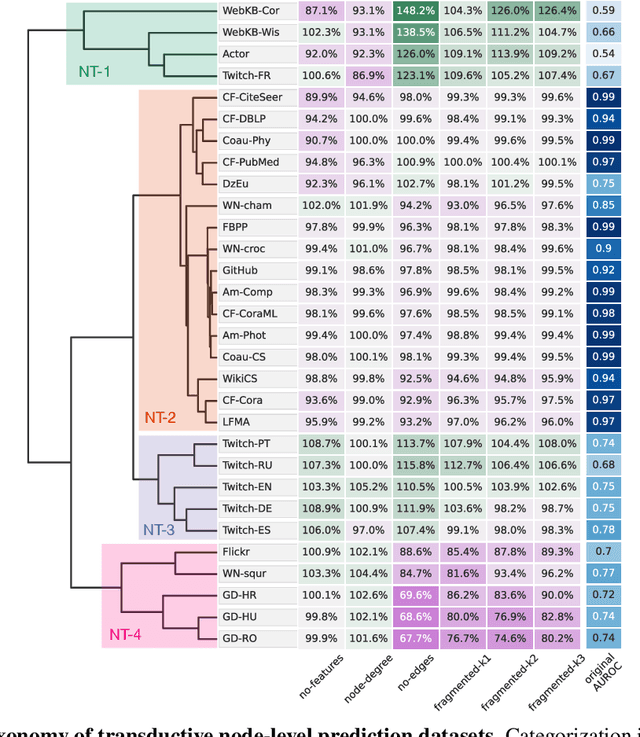
Graph neural networks (GNNs) have attracted much attention due to their ability to leverage the intrinsic geometries of the underlying data. Although many different types of GNN models have been developed, with many benchmarking procedures to demonstrate the superiority of one GNN model over the others, there is a lack of systematic understanding of the underlying benchmarking datasets, and what aspects of the model are being tested. Here, we provide a principled approach to taxonomize graph benchmarking datasets by carefully designing a collection of graph perturbations to probe the essential data characteristics that GNN models leverage to perform predictions. Our data-driven taxonomization of graph datasets provides a new understanding of critical dataset characteristics that will enable better model evaluation and the development of more specialized GNN models.

A Hybrid Scattering Transform for Signals with Isolated Singularities

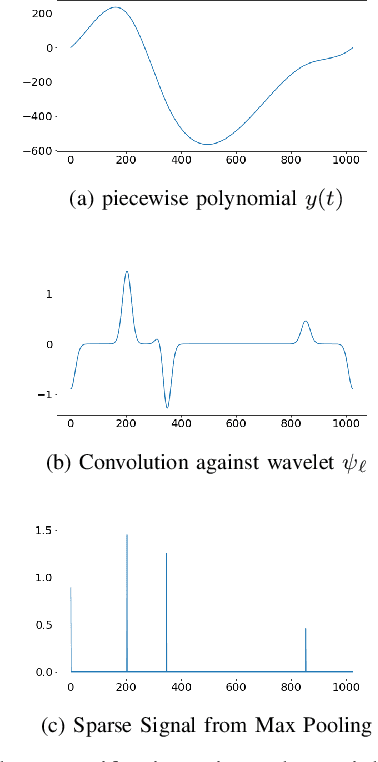
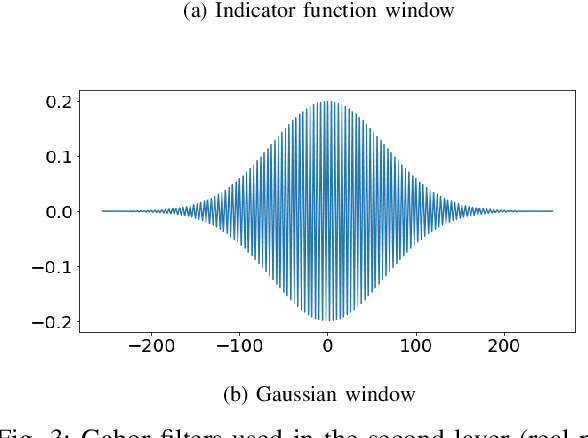
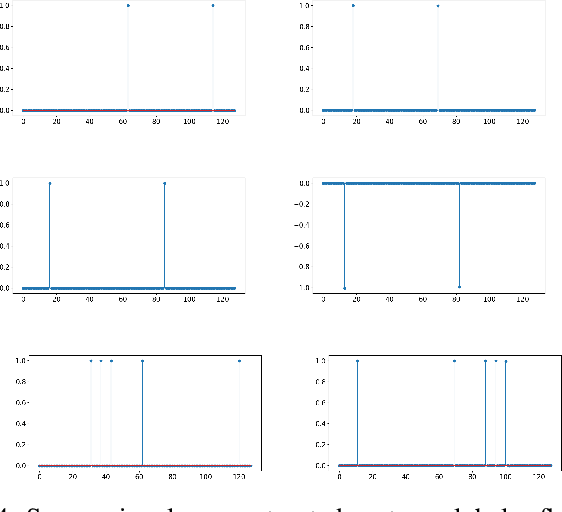
The scattering transform is a wavelet-based model of Convolutional Neural Networks originally introduced by S. Mallat. Mallat's analysis shows that this network has desirable stability and invariance guarantees and therefore helps explain the observation that the filters learned by early layers of a Convolutional Neural Network typically resemble wavelets. Our aim is to understand what sort of filters should be used in the later layers of the network. Towards this end, we propose a two-layer hybrid scattering transform. In our first layer, we convolve the input signal with a wavelet filter transform to promote sparsity, and, in the second layer, we convolve with a Gabor filter to leverage the sparsity created by the first layer. We show that these measurements characterize information about signals with isolated singularities. We also show that the Gabor measurements used in the second layer can be used to synthesize sparse signals such as those produced by the first layer.

Accurately Modeling Biased Random Walks on Weighted Graphs Using $\textit{Node2vec+}$

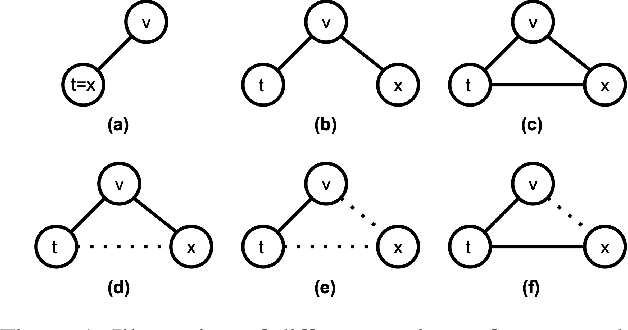
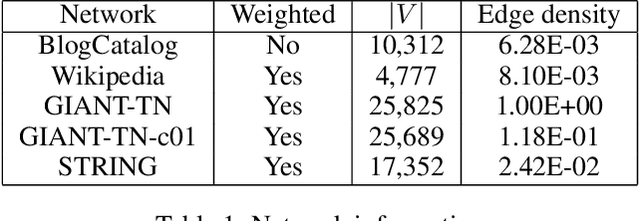
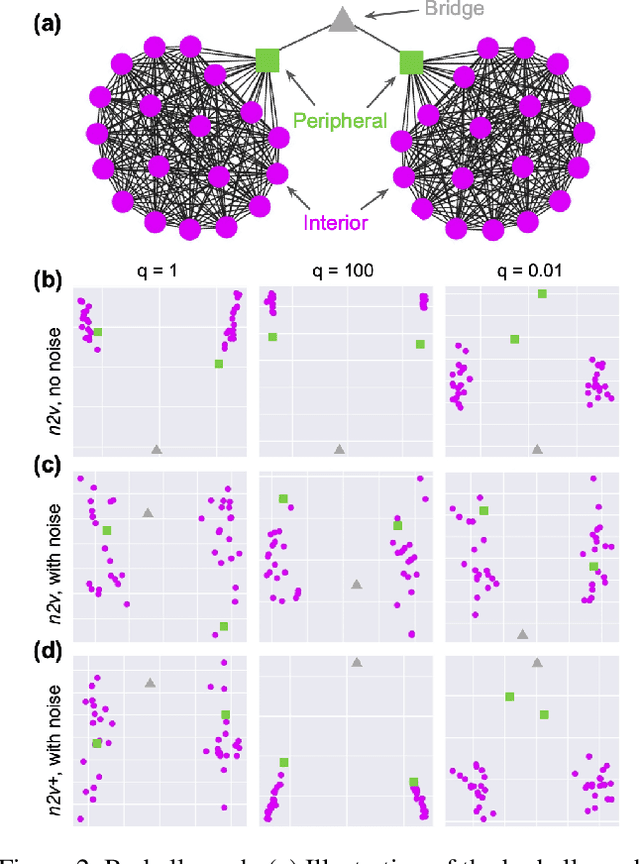
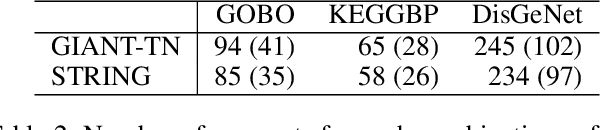
Node embedding is a powerful approach for representing the structural role of each node in a graph. $\textit{Node2vec}$ is a widely used method for node embedding that works by exploring the local neighborhoods via biased random walks on the graph. However, $\textit{node2vec}$ does not consider edge weights when computing walk biases. This intrinsic limitation prevents $\textit{node2vec}$ from leveraging all the information in weighted graphs and, in turn, limits its application to many real-world networks that are weighted and dense. Here, we naturally extend $\textit{node2vec}$ to $\textit{node2vec+}$ in a way that accounts for edge weights when calculating walk biases, but which reduces to $\textit{node2vec}$ in the cases of unweighted graphs or unbiased walks. We empirically show that $\textit{node2vec+}$ is more robust to additive noise than $\textit{node2vec}$ in weighted graphs using two synthetic datasets. We also demonstrate that $\textit{node2vec+}$ significantly outperforms $\textit{node2vec}$ on a commonly benchmarked multi-label dataset (Wikipedia). Furthermore, we test $\textit{node2vec+}$ against GCN and GraphSAGE using various challenging gene classification tasks on two protein-protein interaction networks. Despite some clear advantages of GCN and GraphSAGE, they show comparable performance with $\textit{node2vec+}$. Finally, $\textit{node2vec+}$ can be used as a general approach for generating biased random walks, benefiting all existing methods built on top of $\textit{node2vec}$. $\textit{Node2vec+}$ is implemented as part of $\texttt{PecanPy}$, which is available at https://github.com/krishnanlab/PecanPy .