Implicit Regularization for Tubal Tensor Factorizations via Gradient Descent

We provide a rigorous analysis of implicit regularization in an overparametrized tensor factorization problem beyond the lazy training regime. For matrix factorization problems, this phenomenon has been studied in a number of works. A particular challenge has been to design universal initialization strategies which provably lead to implicit regularization in gradient-descent methods. At the same time, it has been argued by Cohen et. al. 2016 that more general classes of neural networks can be captured by considering tensor factorizations. However, in the tensor case, implicit regularization has only been rigorously established for gradient flow or in the lazy training regime. In this paper, we prove the first tensor result of its kind for gradient descent rather than gradient flow. We focus on the tubal tensor product and the associated notion of low tubal rank, encouraged by the relevance of this model for image data. We establish that gradient descent in an overparametrized tensor factorization model with a small random initialization exhibits an implicit bias towards solutions of low tubal rank. Our theoretical findings are illustrated in an extensive set of numerical simulations show-casing the dynamics predicted by our theory as well as the crucial role of using a small random initialization.

Neural Network Approximation of Lipschitz Functions in High Dimensions with Applications to Inverse Problems

The remarkable successes of neural networks in a huge variety of inverse problems have fueled their adoption in disciplines ranging from medical imaging to seismic analysis over the past decade. However, the high dimensionality of such inverse problems has simultaneously left current theory, which predicts that networks should scale exponentially in the dimension of the problem, unable to explain why the seemingly small networks used in these settings work as well as they do in practice. To reduce this gap between theory and practice, a general method for bounding the complexity required for a neural network to approximate a Lipschitz function on a high-dimensional set with a low-complexity structure is provided herein. The approach is based on the observation that the existence of a linear Johnson-Lindenstrauss embedding $\mathbf{A} \in \mathbb{R}^{d \times D}$ of a given high-dimensional set $\mathcal{S} \subset \mathbb{R}^D$ into a low dimensional cube $[-M,M]^d$ implies that for any Lipschitz function $f : \mathcal{S}\to \mathbb{R}^p$, there exists a Lipschitz function $g : [-M,M]^d \to \mathbb{R}^p$ such that $g(\mathbf{A}\mathbf{x}) = f(\mathbf{x})$ for all $\mathbf{x} \in \mathcal{S}$. Hence, if one has a neural network which approximates $g : [-M,M]^d \to \mathbb{R}^p$, then a layer can be added which implements the JL embedding $\mathbf{A}$ to obtain a neural network which approximates $f : \mathcal{S} \to \mathbb{R}^p$. By pairing JL embedding results along with results on approximation of Lipschitz functions by neural networks, one then obtains results which bound the complexity required for a neural network to approximate Lipschitz functions on high dimensional sets. The end result is a general theoretical framework which can then be used to better explain the observed empirical successes of smaller networks in a wider variety of inverse problems than current theory allows.

A Hybrid Scattering Transform for Signals with Isolated Singularities

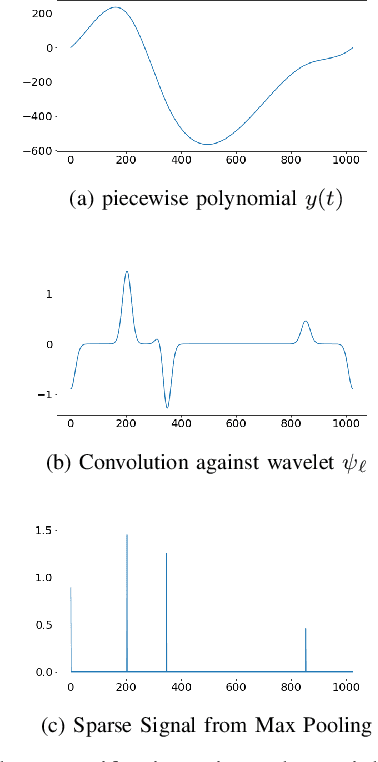
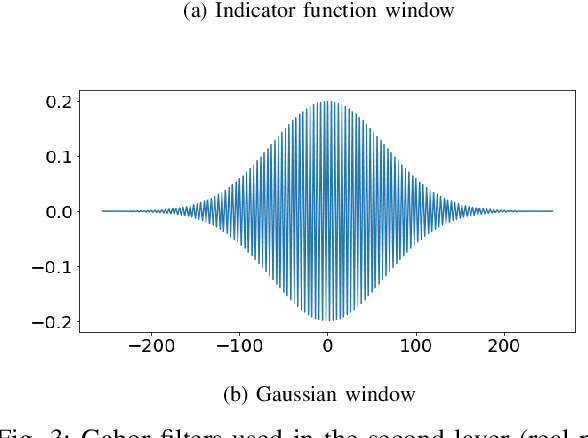
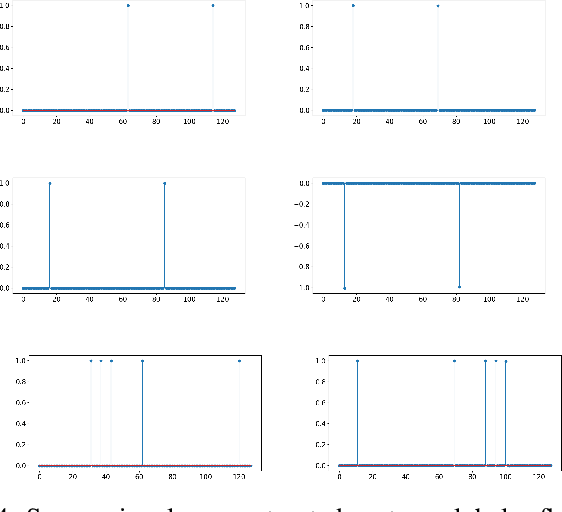
The scattering transform is a wavelet-based model of Convolutional Neural Networks originally introduced by S. Mallat. Mallat's analysis shows that this network has desirable stability and invariance guarantees and therefore helps explain the observation that the filters learned by early layers of a Convolutional Neural Network typically resemble wavelets. Our aim is to understand what sort of filters should be used in the later layers of the network. Towards this end, we propose a two-layer hybrid scattering transform. In our first layer, we convolve the input signal with a wavelet filter transform to promote sparsity, and, in the second layer, we convolve with a Gabor filter to leverage the sparsity created by the first layer. We show that these measurements characterize information about signals with isolated singularities. We also show that the Gabor measurements used in the second layer can be used to synthesize sparse signals such as those produced by the first layer.