Implicit Regularization for Tubal Tensor Factorizations via Gradient Descent

We provide a rigorous analysis of implicit regularization in an overparametrized tensor factorization problem beyond the lazy training regime. For matrix factorization problems, this phenomenon has been studied in a number of works. A particular challenge has been to design universal initialization strategies which provably lead to implicit regularization in gradient-descent methods. At the same time, it has been argued by Cohen et. al. 2016 that more general classes of neural networks can be captured by considering tensor factorizations. However, in the tensor case, implicit regularization has only been rigorously established for gradient flow or in the lazy training regime. In this paper, we prove the first tensor result of its kind for gradient descent rather than gradient flow. We focus on the tubal tensor product and the associated notion of low tubal rank, encouraged by the relevance of this model for image data. We establish that gradient descent in an overparametrized tensor factorization model with a small random initialization exhibits an implicit bias towards solutions of low tubal rank. Our theoretical findings are illustrated in an extensive set of numerical simulations show-casing the dynamics predicted by our theory as well as the crucial role of using a small random initialization.

Neural Network Approximation of Lipschitz Functions in High Dimensions with Applications to Inverse Problems

The remarkable successes of neural networks in a huge variety of inverse problems have fueled their adoption in disciplines ranging from medical imaging to seismic analysis over the past decade. However, the high dimensionality of such inverse problems has simultaneously left current theory, which predicts that networks should scale exponentially in the dimension of the problem, unable to explain why the seemingly small networks used in these settings work as well as they do in practice. To reduce this gap between theory and practice, a general method for bounding the complexity required for a neural network to approximate a Lipschitz function on a high-dimensional set with a low-complexity structure is provided herein. The approach is based on the observation that the existence of a linear Johnson-Lindenstrauss embedding $\mathbf{A} \in \mathbb{R}^{d \times D}$ of a given high-dimensional set $\mathcal{S} \subset \mathbb{R}^D$ into a low dimensional cube $[-M,M]^d$ implies that for any Lipschitz function $f : \mathcal{S}\to \mathbb{R}^p$, there exists a Lipschitz function $g : [-M,M]^d \to \mathbb{R}^p$ such that $g(\mathbf{A}\mathbf{x}) = f(\mathbf{x})$ for all $\mathbf{x} \in \mathcal{S}$. Hence, if one has a neural network which approximates $g : [-M,M]^d \to \mathbb{R}^p$, then a layer can be added which implements the JL embedding $\mathbf{A}$ to obtain a neural network which approximates $f : \mathcal{S} \to \mathbb{R}^p$. By pairing JL embedding results along with results on approximation of Lipschitz functions by neural networks, one then obtains results which bound the complexity required for a neural network to approximate Lipschitz functions on high dimensional sets. The end result is a general theoretical framework which can then be used to better explain the observed empirical successes of smaller networks in a wider variety of inverse problems than current theory allows.

Broadband Beamforming via Linear Embedding

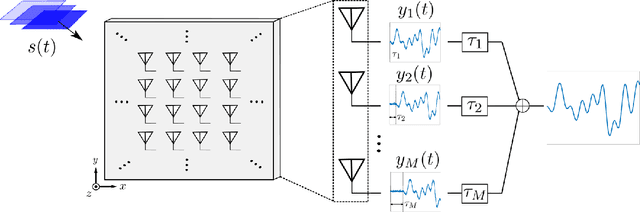
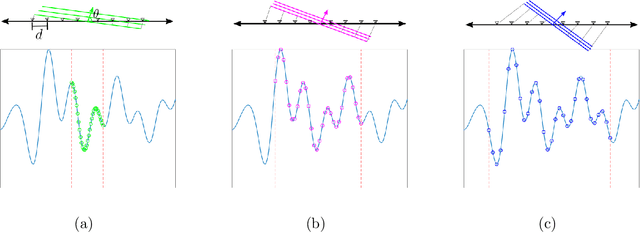
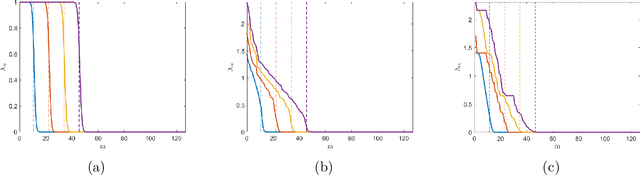
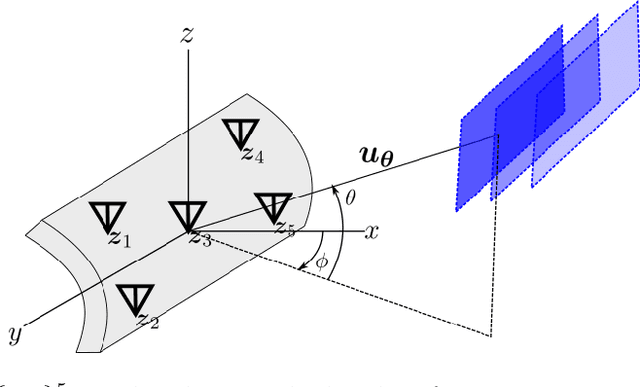
In modern applications multi-sensor arrays are subject to an ever-present demand to accommodate signals with higher bandwidths. Standard methods for broadband beamforming, namely digital beamforming and true-time delay, are difficult and expensive to implement at scale. In this work, we explore an alternative method of broadband beamforming that uses a set of linear measurements and a robust low-dimensional signal subspace model. The linear measurements, taken directly from the sensors, serve as a method for dimensionality reduction and serve to limit the array readout. From these embedded samples, we show how the original samples can be recovered to within a provably small residual error using a Slepian subspace model. Previous work in multi-sensor array subspace models have largely analyzed performance from a qualitative or asymptotic perspective. In contrast, we give quantitative estimates of how well different dimensionality reduction strategies preserve the array gain. We also show how spatial and temporal correlations can be used to relax the standard Nyquist sampling criterion, how recovery can be achieved through fast algorithms, and how "hardware friendly" linear measurements can be designed.

Harmless interpolation in regression and classification with structured features

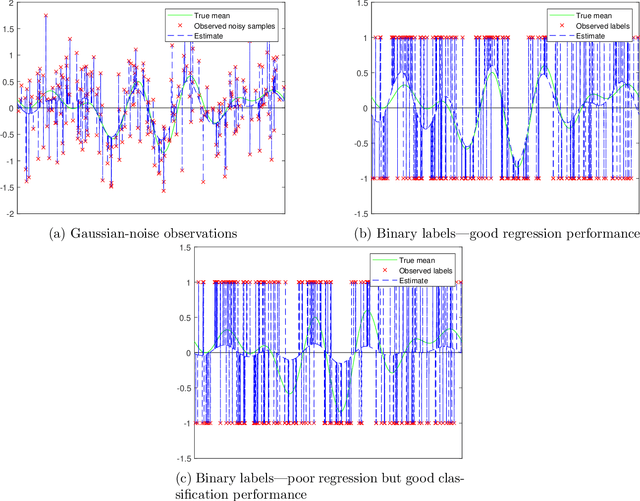
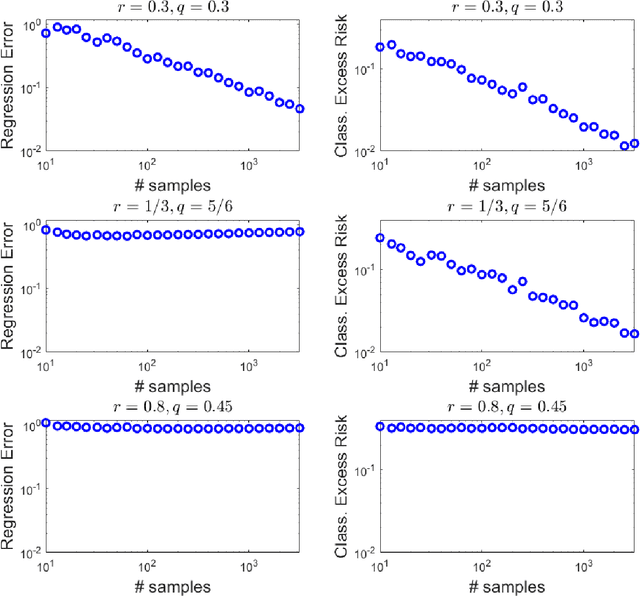
Overparametrized neural networks tend to perfectly fit noisy training data yet generalize well on test data. Inspired by this empirical observation, recent work has sought to understand this phenomenon of benign overfitting or harmless interpolation in the much simpler linear model. Previous theoretical work critically assumes that either the data features are statistically independent or the input data is high-dimensional; this precludes general nonparametric settings with structured feature maps. In this paper, we present a general and flexible framework for upper bounding regression and classification risk in a reproducing kernel Hilbert space. A key contribution is that our framework describes precise sufficient conditions on the data Gram matrix under which harmless interpolation occurs. Our results recover prior independent-features results (with a much simpler analysis), but they furthermore show that harmless interpolation can occur in more general settings such as features that are a bounded orthonormal system. Furthermore, our results show an asymptotic separation between classification and regression performance in a manner that was previously only shown for Gaussian features.

Thomson's Multitaper Method Revisited

Thomson's multitaper method estimates the power spectrum of a signal from $N$ equally spaced samples by averaging $K$ tapered periodograms. Discrete prolate spheroidal sequences (DPSS) are used as tapers since they provide excellent protection against spectral leakage. Thomson's multitaper method is widely used in applications, but most of the existing theory is qualitative or asymptotic. Furthermore, many practitioners use a DPSS bandwidth $W$ and number of tapers that are smaller than what the theory suggests is optimal because the computational requirements increase with the number of tapers. We revisit Thomson's multitaper method from a linear algebra perspective involving subspace projections. This provides additional insight and helps us establish nonasymptotic bounds on some statistical properties of the multitaper spectral estimate, which are similar to existing asymptotic results. We show using $K=2NW-O(\log(NW))$ tapers instead of the traditional $2NW-O(1)$ tapers better protects against spectral leakage, especially when the power spectrum has a high dynamic range. Our perspective also allows us to derive an $\epsilon$-approximation to the multitaper spectral estimate which can be evaluated on a grid of frequencies using $O(\log(NW)\log\tfrac{1}{\epsilon})$ FFTs instead of $K=O(NW)$ FFTs. This is useful in problems where many samples are taken, and thus, using many tapers is desirable.