Distance preservation in state-space methods for detecting causal interactions in dynamical systems

We analyze the popular ``state-space'' class of algorithms for detecting casual interaction in coupled dynamical systems. These algorithms are often justified by Takens' embedding theorem, which provides conditions under which relationships involving attractors and their delay embeddings are continuous. In practice, however, state-space methods often do not directly test continuity, but rather the stronger property of how these relationships preserve inter-point distances. This paper theoretically and empirically explores state-space algorithms explicitly from the perspective of distance preservation. We first derive basic theoretical guarantees applicable to simple coupled systems, providing conditions under which the distance preservation of a certain map reveals underlying causal structure. Second, we demonstrate empirically that typical coupled systems do not satisfy distance preservation assumptions. Taken together, our results underline the dependence of state-space algorithms on intrinsic system properties and the relationship between the system and the function used to measure it -- properties that are not directly associated with causal interaction.

Broadband Beamforming via Linear Embedding

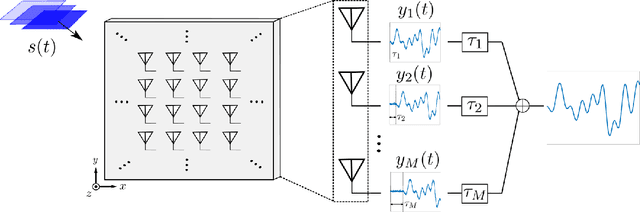
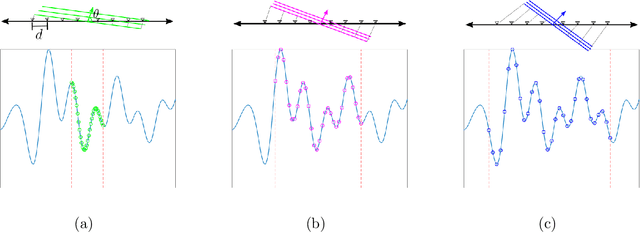
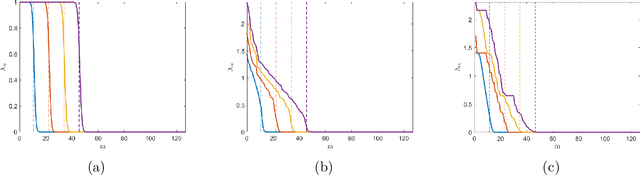
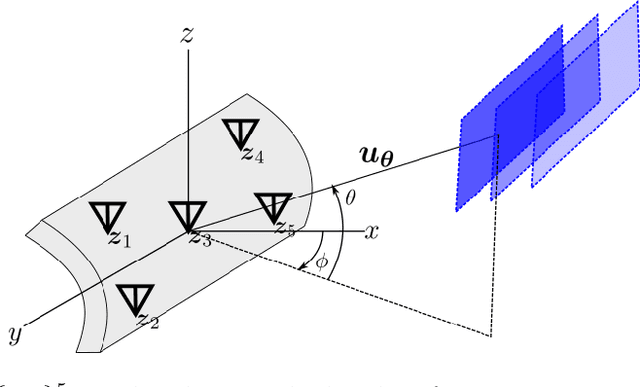
In modern applications multi-sensor arrays are subject to an ever-present demand to accommodate signals with higher bandwidths. Standard methods for broadband beamforming, namely digital beamforming and true-time delay, are difficult and expensive to implement at scale. In this work, we explore an alternative method of broadband beamforming that uses a set of linear measurements and a robust low-dimensional signal subspace model. The linear measurements, taken directly from the sensors, serve as a method for dimensionality reduction and serve to limit the array readout. From these embedded samples, we show how the original samples can be recovered to within a provably small residual error using a Slepian subspace model. Previous work in multi-sensor array subspace models have largely analyzed performance from a qualitative or asymptotic perspective. In contrast, we give quantitative estimates of how well different dimensionality reduction strategies preserve the array gain. We also show how spatial and temporal correlations can be used to relax the standard Nyquist sampling criterion, how recovery can be achieved through fast algorithms, and how "hardware friendly" linear measurements can be designed.

Generative causal explanations of black-box classifiers

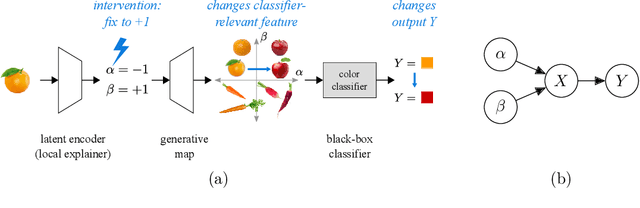
We develop a method for generating causal post-hoc explanations of black-box classifiers based on a learned low-dimensional representation of the data. The explanation is causal in the sense that changing learned latent factors produces a change in the classifier output statistics. To construct these explanations, we design a learning framework that leverages a generative model and information-theoretic measures of causal influence. Our objective function encourages both the generative model to faithfully represent the data distribution and the latent factors to have a large causal influence on the classifier output. Our method learns both global and local explanations, is compatible with any classifier that admits class probabilities and a gradient, and does not require labeled attributes or knowledge of causal structure. Using carefully controlled test cases, we provide intuition that illuminates the function of our causal objective. We then demonstrate the practical utility of our method on image recognition tasks.

Sample complexity and effective dimension for regression on manifolds

We consider the theory of regression on a manifold using reproducing kernel Hilbert space methods. Manifold models arise in a wide variety of modern machine learning problems, and our goal is to help understand the effectiveness of various implicit and explicit dimensionality-reduction methods that exploit manifold structure. Our first key contribution is to establish a novel nonasymptotic version of the Weyl law from differential geometry. From this we are able to show that certain spaces of smooth functions on a manifold are effectively finite-dimensional, with a complexity that scales according to the manifold dimension rather than any ambient data dimension. Finally, we show that given (potentially noisy) function values taken uniformly at random over a manifold, a kernel regression estimator (derived from the spectral decomposition of the manifold) yields error bounds that are controlled by the effective dimension.

A unified framework for manifold landmarking

The success of semi-supervised manifold learning is highly dependent on the quality of the labeled samples. Active manifold learning aims to select and label representative landmarks on a manifold from a given set of samples to improve semi-supervised manifold learning. In this paper, we propose a novel active manifold learning method based on a unified framework of manifold landmarking. In particular, our method combines geometric manifold landmarking methods with algebraic ones. We achieve this by using the Gershgorin circle theorem to construct an upper bound on the learning error that depends on the landmarks and the manifold's alignment matrix in a way that captures both the geometric and algebraic criteria. We then attempt to select landmarks so as to minimize this bound by iteratively deleting the Gershgorin circles corresponding to the selected landmarks. We also analyze the complexity, scalability, and robustness of our method through simulations, and demonstrate its superiority compared to existing methods. Experiments in regression and classification further verify that our method performs better than its competitors.