Justin Romberg
A Fast Broadband Beamspace Transformation
Dec 09, 2025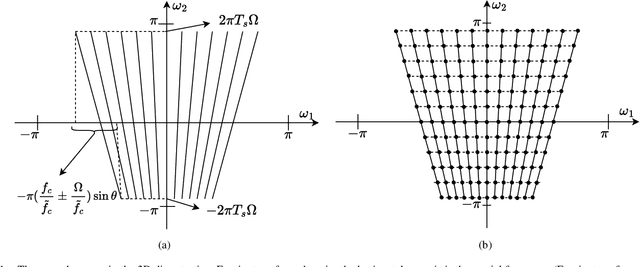
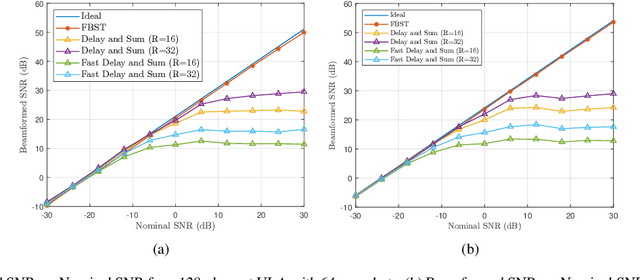
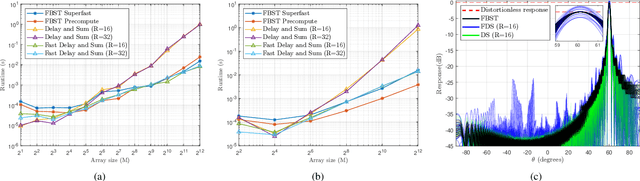
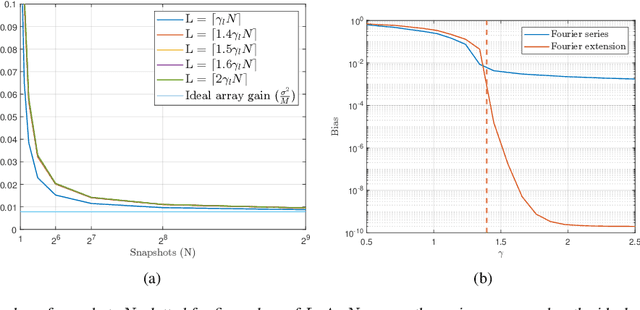
Abstract:We present a new computationally efficient method for multi-beamforming in the broadband setting. Our "fast beamspace transformation" forms $B$ beams from $M$ sensor outputs using a number of operations per sample that scales linearly (to within logarithmic factors) with $M$ when $B\sim M$. While the narrowband version of this transformation can be performed efficiently with a spatial fast Fourier transform, the broadband setting requires coherent processing of multiple array snapshots simultaneously. Our algorithm works by taking $N$ samples off of each of $M$ sensors and encoding the sensor outputs into a set of coefficients using a special non-uniform spaced Fourier transform. From these coefficients, each beam is formed by solving a small system of equations that has Toeplitz structure. The total runtime complexity is $\mathcal{O}(M\log N+B\log N)$ operations per sample, exhibiting essentially the same scaling as in the narrowband case and vastly outperforming broadband beamformers based on delay and sum whose computations scale as $\mathcal{O}(MB)$. Alongside a careful mathematical formulation and analysis of our fast broadband beamspace transform, we provide a host of numerical experiments demonstrating the algorithm's favorable computational scaling and high accuracy. Finally, we demonstrate how tasks such as interpolating to ``off-grid" angles and nulling an interferer are more computationally efficient when performed directly in beamspace.
A general technique for approximating high-dimensional empirical kernel matrices
Nov 05, 2025Abstract:We present simple, user-friendly bounds for the expected operator norm of a random kernel matrix under general conditions on the kernel function $k(\cdot,\cdot)$. Our approach uses decoupling results for U-statistics and the non-commutative Khintchine inequality to obtain upper and lower bounds depending only on scalar statistics of the kernel function and a ``correlation kernel'' matrix corresponding to $k(\cdot,\cdot)$. We then apply our method to provide new, tighter approximations for inner-product kernel matrices on general high-dimensional data, where the sample size and data dimension are polynomially related. Our method obtains simplified proofs of existing results that rely on the moment method and combinatorial arguments while also providing novel approximation results for the case of anisotropic Gaussian data. Finally, using similar techniques to our approximation result, we show a tighter lower bound on the bias of kernel regression with anisotropic Gaussian data.
Global Convergence of Adaptive Sensing for Principal Eigenvector Estimation
May 16, 2025Abstract:This paper addresses the challenge of efficient principal component analysis (PCA) in high-dimensional spaces by analyzing a compressively sampled variant of Oja's algorithm with adaptive sensing. Traditional PCA methods incur substantial computational costs that scale poorly with data dimensionality, whereas subspace tracking algorithms like Oja's offer more efficient alternatives but typically require full-dimensional observations. We analyze a variant where, at each iteration, only two compressed measurements are taken: one in the direction of the current estimate and one in a random orthogonal direction. We prove that this adaptive sensing approach achieves global convergence in the presence of noise when tracking the leading eigenvector of a datastream with eigengap $\Delta=\lambda_1-\lambda_2$. Our theoretical analysis demonstrates that the algorithm experiences two phases: (1) a warmup phase requiring $O(\lambda_1\lambda_2d^2/\Delta^2)$ iterations to achieve a constant-level alignment with the true eigenvector, followed by (2) a local convergence phase where the sine alignment error decays at a rate of $O(\lambda_1\lambda_2d^2/\Delta^2 t)$ for iterations $t$. The guarantee aligns with existing minimax lower bounds with an added factor of $d$ due to the compressive sampling. This work provides the first convergence guarantees in adaptive sensing for subspace tracking with noise. Our proof technique is also considerably simpler than those in prior works. The results have important implications for applications where acquiring full-dimensional samples is challenging or costly.
Accelerating Multi-Task Temporal Difference Learning under Low-Rank Representation
Mar 03, 2025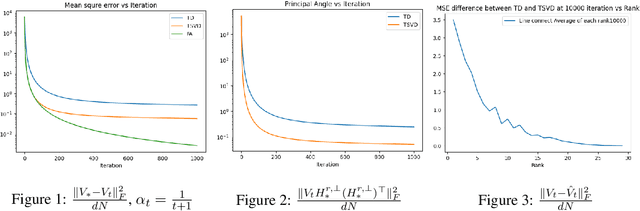
Abstract:We study policy evaluation problems in multi-task reinforcement learning (RL) under a low-rank representation setting. In this setting, we are given $N$ learning tasks where the corresponding value function of these tasks lie in an $r$-dimensional subspace, with $r<N$. One can apply the classic temporal-difference (TD) learning method for solving these problems where this method learns the value function of each task independently. In this paper, we are interested in understanding whether one can exploit the low-rank structure of the multi-task setting to accelerate the performance of TD learning. To answer this question, we propose a new variant of TD learning method, where we integrate the so-called truncated singular value decomposition step into the update of TD learning. This additional step will enable TD learning to exploit the dominant directions due to the low rank structure to update the iterates, therefore, improving its performance. Our empirical results show that the proposed method significantly outperforms the classic TD learning, where the performance gap increases as the rank $r$ decreases. From the theoretical point of view, introducing the truncated singular value decomposition step into TD learning might cause an instability on the updates. We provide a theoretical result showing that the instability does not happen. Specifically, we prove that the proposed method converges at a rate $\mathcal{O}(\frac{\ln(t)}{t})$, where $t$ is the number of iterations. This rate matches that of the standard TD learning.
Rapid Grassmannian Averaging with Chebyshev Polynomials
Oct 11, 2024

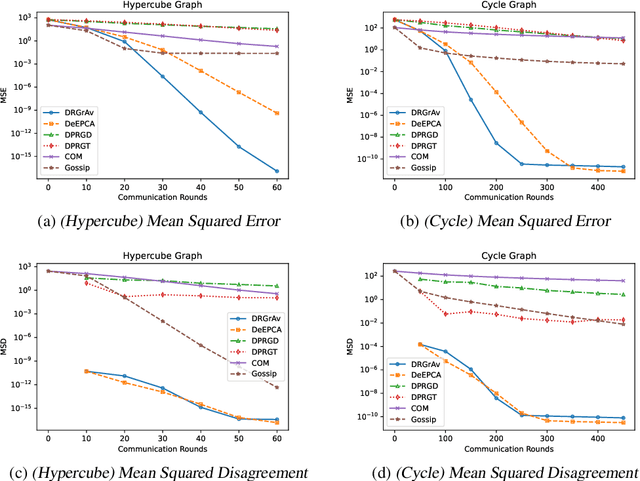

Abstract:We propose new algorithms to efficiently average a collection of points on a Grassmannian manifold in both the centralized and decentralized settings. Grassmannian points are used ubiquitously in machine learning, computer vision, and signal processing to represent data through (often low-dimensional) subspaces. While averaging these points is crucial to many tasks (especially in the decentralized setting), existing methods unfortunately remain computationally expensive due to the non-Euclidean geometry of the manifold. Our proposed algorithms, Rapid Grassmannian Averaging (RGrAv) and Decentralized Rapid Grassmannian Averaging (DRGrAv), overcome this challenge by leveraging the spectral structure of the problem to rapidly compute an average using only small matrix multiplications and QR factorizations. We provide a theoretical guarantee of optimality and present numerical experiments which demonstrate that our algorithms outperform state-of-the-art methods in providing high accuracy solutions in minimal time. Additional experiments showcase the versatility of our algorithms to tasks such as K-means clustering on video motion data, establishing RGrAv and DRGrAv as powerful tools for generic Grassmannian averaging.
Robust Broadband Beamforming using Bilinear Programming
Jun 24, 2024



Abstract:We introduce a new method for robust beamforming, where the goal is to estimate a signal from array samples when there is uncertainty in the angle of arrival. Our method offers state-of-the-art performance on narrowband signals and is naturally applied to broadband signals. Our beamformer operates by treating the forward model for the array samples as unknown. We show that the "true" forward model lies in the linear span of a small number of fixed linear systems. As a result, we can estimate the forward operator and the signal simultaneously by solving a bilinear inverse problem using least squares. Our numerical experiments show that if the angle of arrival is known to only be within an interval of reasonable size, there is very little loss in estimation performance compared to the case where the angle is known exactly.
Real-time Digital RF Emulation -- I: The Direct Path Computational Model
Jun 13, 2024



Abstract:In this paper we consider the problem of developing a computational model for emulating an RF channel. The motivation for this is that an accurate and scalable emulator has the potential to minimize the need for field testing, which is expensive, slow, and difficult to replicate. Traditionally, emulators are built using a tapped delay line model where long filters modeling the physical interactions of objects are implemented directly. For an emulation scenario consisting of $M$ objects all interacting with one another, the tapped delay line model's computational requirements scale as $O(M^3)$ per sample: there are $O(M^2)$ channels, each with $O(M)$ complexity. In this paper, we develop a new ``direct path" model that, while remaining physically faithful, allows us to carefully factor the emulator operations, resulting in an $O(M^2)$ per sample scaling of the computational requirements. The impact of this is drastic, a $200$ object scenario sees about a $100\times$ reduction in the number of per sample computations. Furthermore, the direct path model gives us a natural way to distribute the computations for an emulation: each object is mapped to a computational node, and these nodes are networked in a fully connected communication graph. Alongside a discussion of the model and the physical phenomena it emulates, we show how to efficiently parameterize antenna responses and scattering profiles within this direct path framework. To verify the model and demonstrate its viability in hardware, we provide several numerical experiments produced using a cycle level C++ simulator of a hardware implementation of the model.
Real-time Digital RF Emulation -- II: A Near Memory Custom Accelerator
Jun 13, 2024



Abstract:A near memory hardware accelerator, based on a novel direct path computational model, for real-time emulation of radio frequency systems is demonstrated. Our evaluation of hardware performance uses both application-specific integrated circuits (ASIC) and field programmable gate arrays (FPGA) methodologies: 1). The ASIC testchip implementation, using TSMC 28nm CMOS, leverages distributed autonomous control to extract concurrency in compute as well as low latency. It achieves a $518$ MHz per channel bandwidth in a prototype $4$-node system. The maximum emulation range supported in this paradigm is $9.5$ km with $0.24$ $\mu$s of per-sample emulation latency. 2). The FPGA-based implementation, evaluated on a Xilinx ZCU104 board, demonstrates a $9$-node test case (two Transmitters, one Receiver, and $6$ passive reflectors) with an emulation range of $1.13$ km to $27.3$ km at $215$ MHz bandwidth.
Precise asymptotics of reweighted least-squares algorithms for linear diagonal networks
Jun 04, 2024Abstract:The classical iteratively reweighted least-squares (IRLS) algorithm aims to recover an unknown signal from linear measurements by performing a sequence of weighted least squares problems, where the weights are recursively updated at each step. Varieties of this algorithm have been shown to achieve favorable empirical performance and theoretical guarantees for sparse recovery and $\ell_p$-norm minimization. Recently, some preliminary connections have also been made between IRLS and certain types of non-convex linear neural network architectures that are observed to exploit low-dimensional structure in high-dimensional linear models. In this work, we provide a unified asymptotic analysis for a family of algorithms that encompasses IRLS, the recently proposed lin-RFM algorithm (which was motivated by feature learning in neural networks), and the alternating minimization algorithm on linear diagonal neural networks. Our analysis operates in a "batched" setting with i.i.d. Gaussian covariates and shows that, with appropriately chosen reweighting policy, the algorithm can achieve favorable performance in only a handful of iterations. We also extend our results to the case of group-sparse recovery and show that leveraging this structure in the reweighting scheme provably improves test error compared to coordinate-wise reweighting.
Natural Policy Gradient and Actor Critic Methods for Constrained Multi-Task Reinforcement Learning
May 03, 2024

Abstract:Multi-task reinforcement learning (RL) aims to find a single policy that effectively solves multiple tasks at the same time. This paper presents a constrained formulation for multi-task RL where the goal is to maximize the average performance of the policy across tasks subject to bounds on the performance in each task. We consider solving this problem both in the centralized setting, where information for all tasks is accessible to a single server, and in the decentralized setting, where a network of agents, each given one task and observing local information, cooperate to find the solution of the globally constrained objective using local communication. We first propose a primal-dual algorithm that provably converges to the globally optimal solution of this constrained formulation under exact gradient evaluations. When the gradient is unknown, we further develop a sampled-based actor-critic algorithm that finds the optimal policy using online samples of state, action, and reward. Finally, we study the extension of the algorithm to the linear function approximation setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge