Stochastic Gradient Descent Jittering for Inverse Problems: Alleviating the Accuracy-Robustness Tradeoff

Inverse problems aim to reconstruct unseen data from corrupted or perturbed measurements. While most work focuses on improving reconstruction quality, generalization accuracy and robustness are equally important, especially for safety-critical applications. Model-based architectures (MBAs), such as loop unrolling methods, are considered more interpretable and achieve better reconstructions. Empirical evidence suggests that MBAs are more robust to perturbations than black-box solvers, but the accuracy-robustness tradeoff in MBAs remains underexplored. In this work, we propose a simple yet effective training scheme for MBAs, called SGD jittering, which injects noise iteration-wise during reconstruction. We theoretically demonstrate that SGD jittering not only generalizes better than the standard mean squared error training but is also more robust to average-case attacks. We validate SGD jittering using denoising toy examples, seismic deconvolution, and single-coil MRI reconstruction. The proposed method achieves cleaner reconstructions for out-of-distribution data and demonstrates enhanced robustness to adversarial attacks.

Robust Broadband Beamforming using Bilinear Programming

We introduce a new method for robust beamforming, where the goal is to estimate a signal from array samples when there is uncertainty in the angle of arrival. Our method offers state-of-the-art performance on narrowband signals and is naturally applied to broadband signals. Our beamformer operates by treating the forward model for the array samples as unknown. We show that the "true" forward model lies in the linear span of a small number of fixed linear systems. As a result, we can estimate the forward operator and the signal simultaneously by solving a bilinear inverse problem using least squares. Our numerical experiments show that if the angle of arrival is known to only be within an interval of reasonable size, there is very little loss in estimation performance compared to the case where the angle is known exactly.

Solving Inverse Problems with Model Mismatch using Untrained Neural Networks within Model-based Architectures

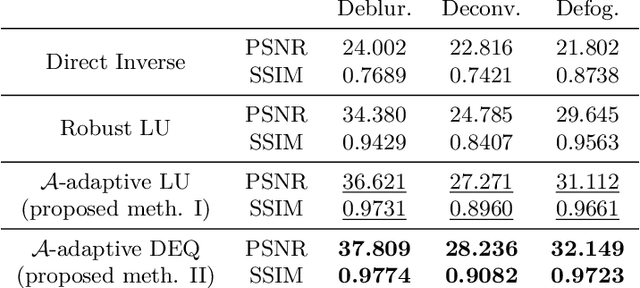
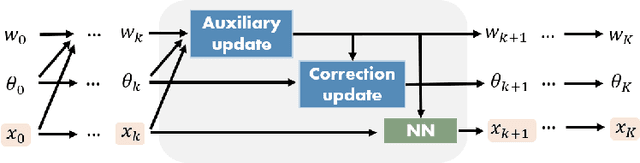
Model-based deep learning methods such as \emph{loop unrolling} (LU) and \emph{deep equilibrium model} (DEQ) extensions offer outstanding performance in solving inverse problems (IP). These methods unroll the optimization iterations into a sequence of neural networks that in effect learn a regularization function from data. While these architectures are currently state-of-the-art in numerous applications, their success heavily relies on the accuracy of the forward model. This assumption can be limiting in many physical applications due to model simplifications or uncertainties in the apparatus. To address forward model mismatch, we introduce an untrained forward model residual block within the model-based architecture to match the data consistency in the measurement domain for each instance. We propose two variants in well-known model-based architectures (LU and DEQ) and prove convergence under mild conditions. The experiments show significant quality improvement in removing artifacts and preserving details across three distinct applications, encompassing both linear and nonlinear inverse problems. Moreover, we highlight reconstruction effectiveness in intermediate steps and showcase robustness to random initialization of the residual block and a higher number of iterations during evaluation.

Slepian Beamforming: Broadband Beamforming using Streaming Least Squares

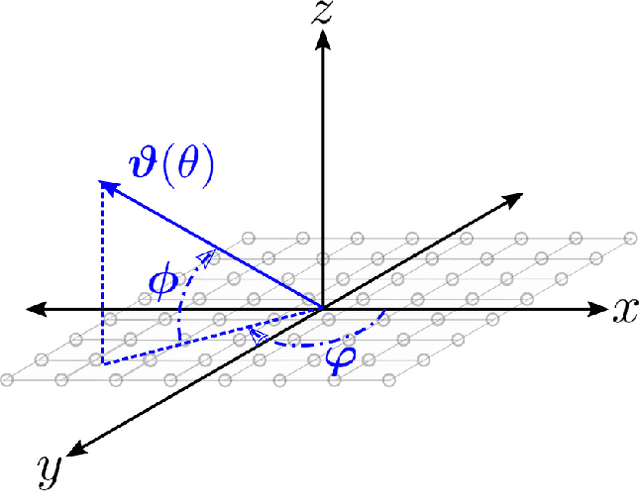
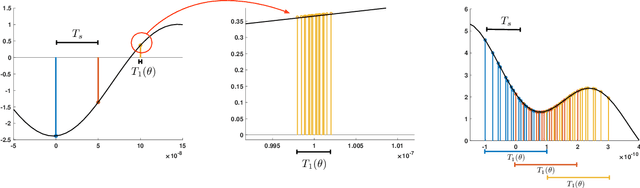
In this paper we revisit the classical problem of estimating a signal as it impinges on a multi-sensor array. We focus on the case where the impinging signal's bandwidth is appreciable and is operating in a broadband regime. Estimating broadband signals, often termed broadband (or wideband) beamforming, is traditionally done through filter and summation, true time delay, or a coupling of the two. Our proposed method deviates substantially from these paradigms in that it requires no notion of filtering or true time delay. We use blocks of samples taken directly from the sensor outputs to fit a robust Slepian subspace model using a least squares approach. We then leverage this model to estimate uniformly spaced samples of the impinging signal. Alongside a careful discussion of this model and how to choose its parameters we show how to fit the model to new blocks of samples as they are received, producing a streaming output. We then go on to show how this method naturally extends to adaptive beamforming scenarios, where we leverage signal statistics to attenuate interfering sources. Finally, we discuss how to use our model to estimate from dimensionality reducing measurements. Accompanying these discussions are extensive numerical experiments establishing that our method outperforms existing filter based approaches while being comparable in terms of computational complexity.

Perceptual adjustment queries and an inverted measurement paradigm for low-rank metric learning

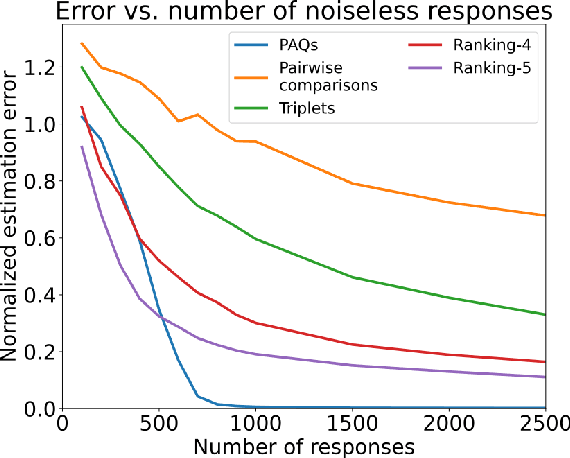
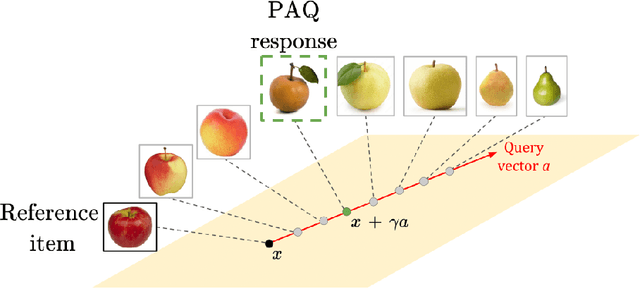
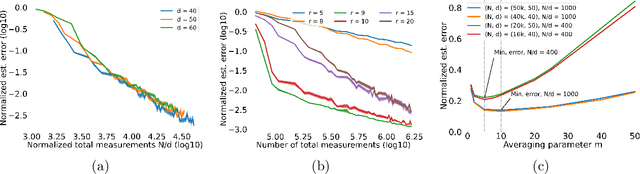
We introduce a new type of query mechanism for collecting human feedback, called the perceptual adjustment query ( PAQ). Being both informative and cognitively lightweight, the PAQ adopts an inverted measurement scheme, and combines advantages from both cardinal and ordinal queries. We showcase the PAQ in the metric learning problem, where we collect PAQ measurements to learn an unknown Mahalanobis distance. This gives rise to a high-dimensional, low-rank matrix estimation problem to which standard matrix estimators cannot be applied. Consequently, we develop a two-stage estimator for metric learning from PAQs, and provide sample complexity guarantees for this estimator. We present numerical simulations demonstrating the performance of the estimator and its notable properties.

Learned Proximal Operator for Solving Seismic Deconvolution Problem

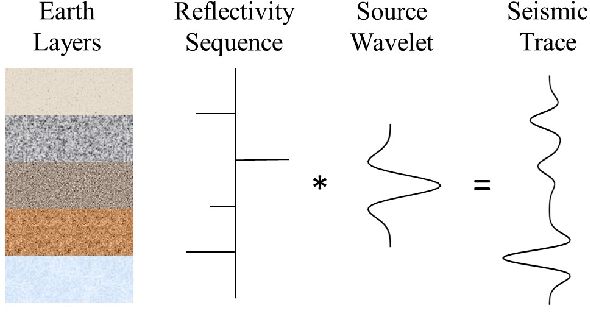
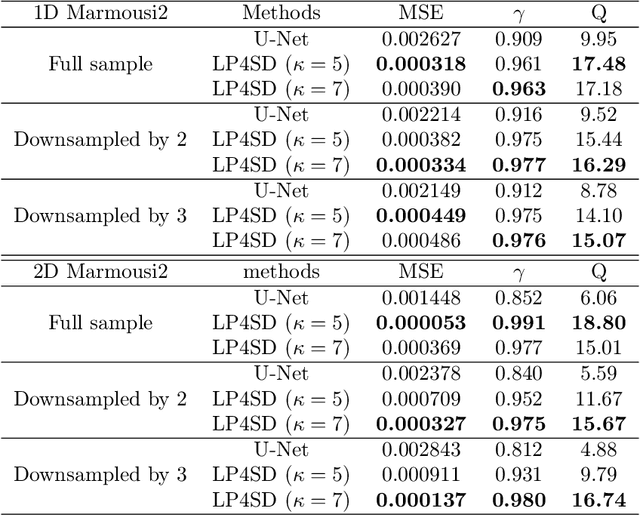
Seismic deconvolution is an essential step in seismic data processing that aims to extract layer information from noisy observed traces. In general, this is an ill-posed problem with non-unique solutions. Due to the sparse nature of the reflectivity sequence, spike-promoting regularizers such as the $\ell_1$-norm are frequently used. They either require rigorous coefficient tuning or strong assumptions about reflectivity, such as assuming reflectivity as sparse signals with known sparsity levels and zero-mean Gaussian noise with known noise levels. To overcome the limitations of traditional regularizers, learning-based regularizers are proposed in the recent past. This paper proposes a Learned Proximal operator for Seismic Deconvolution (LP4SD), which leverages a neural network to learn the proximal operator of a regularizer. LP4SD is trained in a loop unrolled manner and is capable of learning complicated structures from the training data. It is worth mentioning that the network is trained with synthetic data and evaluated on both synthetic and real data. LP4SD is shown to generate better reconstruction results in terms of three different metrics as compared to learning a direct inverse.

New Equivalences Between Interpolation and SVMs: Kernels and Structured Features

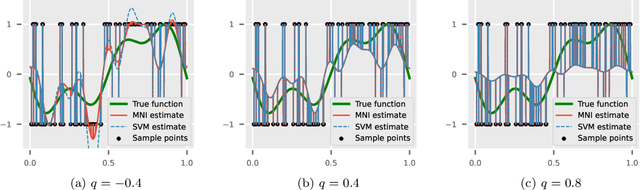
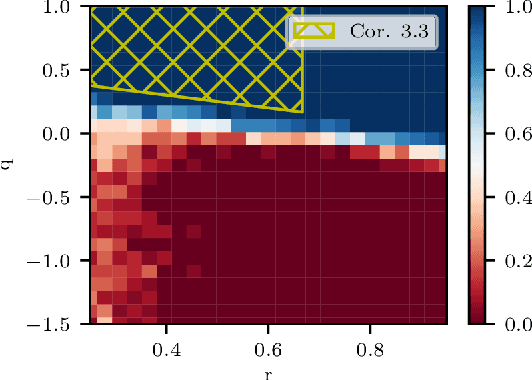
The support vector machine (SVM) is a supervised learning algorithm that finds a maximum-margin linear classifier, often after mapping the data to a high-dimensional feature space via the kernel trick. Recent work has demonstrated that in certain sufficiently overparameterized settings, the SVM decision function coincides exactly with the minimum-norm label interpolant. This phenomenon of support vector proliferation (SVP) is especially interesting because it allows us to understand SVM performance by leveraging recent analyses of harmless interpolation in linear and kernel models. However, previous work on SVP has made restrictive assumptions on the data/feature distribution and spectrum. In this paper, we present a new and flexible analysis framework for proving SVP in an arbitrary reproducing kernel Hilbert space with a flexible class of generative models for the labels. We present conditions for SVP for features in the families of general bounded orthonormal systems (e.g. Fourier features) and independent sub-Gaussian features. In both cases, we show that SVP occurs in many interesting settings not covered by prior work, and we leverage these results to prove novel generalization results for kernel SVM classification.

Loop Unrolled Shallow Equilibrium Regularizer (LUSER) -- A Memory-Efficient Inverse Problem Solver

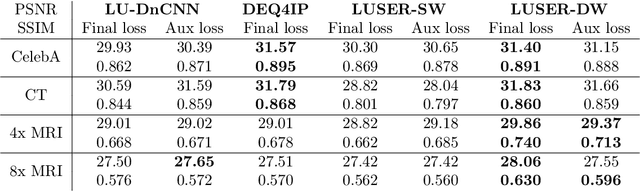
In inverse problems we aim to reconstruct some underlying signal of interest from potentially corrupted and often ill-posed measurements. Classical optimization-based techniques proceed by optimizing a data consistency metric together with a regularizer. Current state-of-the-art machine learning approaches draw inspiration from such techniques by unrolling the iterative updates for an optimization-based solver and then learning a regularizer from data. This loop unrolling (LU) method has shown tremendous success, but often requires a deep model for the best performance leading to high memory costs during training. Thus, to address the balance between computation cost and network expressiveness, we propose an LU algorithm with shallow equilibrium regularizers (LUSER). These implicit models are as expressive as deeper convolutional networks, but far more memory efficient during training. The proposed method is evaluated on image deblurring, computed tomography (CT), as well as single-coil Magnetic Resonance Imaging (MRI) tasks and shows similar, or even better, performance while requiring up to 8 times less computational resources during training when compared against a more typical LU architecture with feedforward convolutional regularizers.

Learning Sinkhorn divergences for supervised change point detection

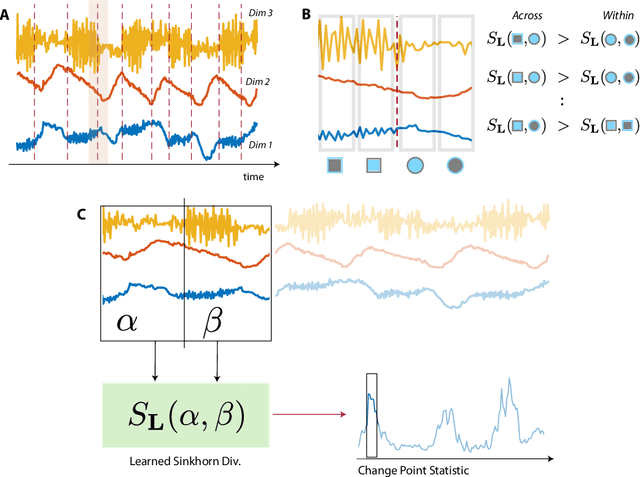
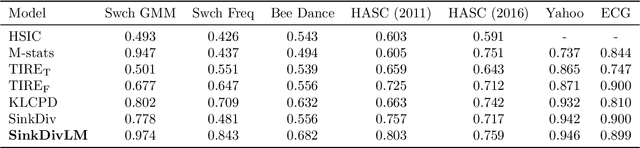
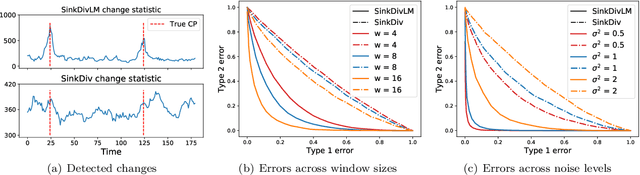
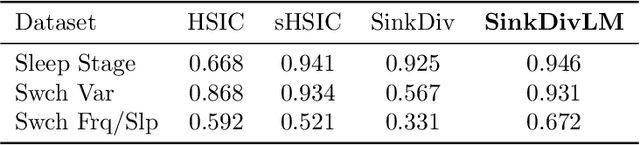
Many modern applications require detecting change points in complex sequential data. Most existing methods for change point detection are unsupervised and, as a consequence, lack any information regarding what kind of changes we want to detect or if some kinds of changes are safe to ignore. This often results in poor change detection performance. We present a novel change point detection framework that uses true change point instances as supervision for learning a ground metric such that Sinkhorn divergences can be then used in two-sample tests on sliding windows to detect change points in an online manner. Our method can be used to learn a sparse metric which can be useful for both feature selection and interpretation in high-dimensional change point detection settings. Experiments on simulated as well as real world sequences show that our proposed method can substantially improve change point detection performance over existing unsupervised change point detection methods using only few labeled change point instances.

Active metric learning and classification using similarity queries

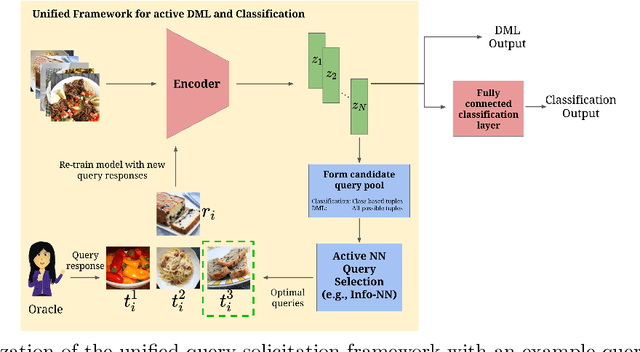
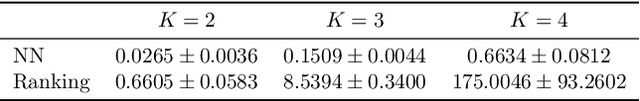
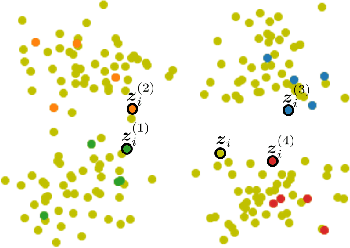
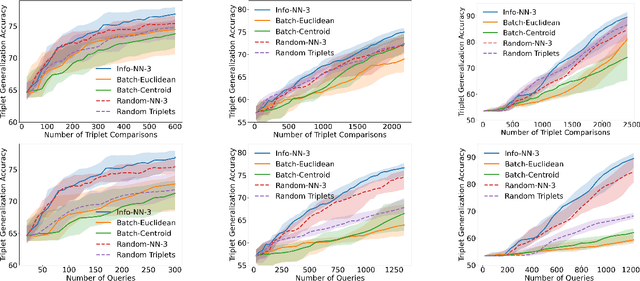
Active learning is commonly used to train label-efficient models by adaptively selecting the most informative queries. However, most active learning strategies are designed to either learn a representation of the data (e.g., embedding or metric learning) or perform well on a task (e.g., classification) on the data. However, many machine learning tasks involve a combination of both representation learning and a task-specific goal. Motivated by this, we propose a novel unified query framework that can be applied to any problem in which a key component is learning a representation of the data that reflects similarity. Our approach builds on similarity or nearest neighbor (NN) queries which seek to select samples that result in improved embeddings. The queries consist of a reference and a set of objects, with an oracle selecting the object most similar (i.e., nearest) to the reference. In order to reduce the number of solicited queries, they are chosen adaptively according to an information theoretic criterion. We demonstrate the effectiveness of the proposed strategy on two tasks -- active metric learning and active classification -- using a variety of synthetic and real world datasets. In particular, we demonstrate that actively selected NN queries outperform recently developed active triplet selection methods in a deep metric learning setting. Further, we show that in classification, actively selecting class labels can be reformulated as a process of selecting the most informative NN query, allowing direct application of our method.