New Equivalences Between Interpolation and SVMs: Kernels and Structured Features
Paper and Code
May 03, 2023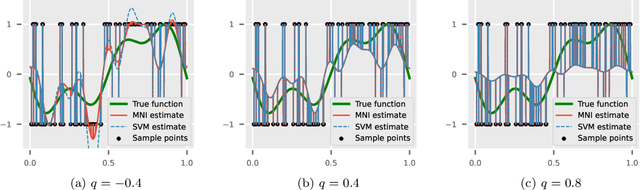

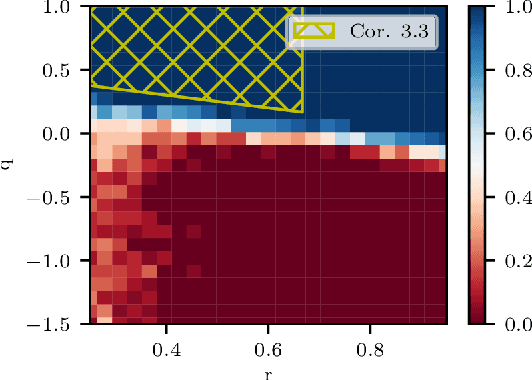
The support vector machine (SVM) is a supervised learning algorithm that finds a maximum-margin linear classifier, often after mapping the data to a high-dimensional feature space via the kernel trick. Recent work has demonstrated that in certain sufficiently overparameterized settings, the SVM decision function coincides exactly with the minimum-norm label interpolant. This phenomenon of support vector proliferation (SVP) is especially interesting because it allows us to understand SVM performance by leveraging recent analyses of harmless interpolation in linear and kernel models. However, previous work on SVP has made restrictive assumptions on the data/feature distribution and spectrum. In this paper, we present a new and flexible analysis framework for proving SVP in an arbitrary reproducing kernel Hilbert space with a flexible class of generative models for the labels. We present conditions for SVP for features in the families of general bounded orthonormal systems (e.g. Fourier features) and independent sub-Gaussian features. In both cases, we show that SVP occurs in many interesting settings not covered by prior work, and we leverage these results to prove novel generalization results for kernel SVM classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge