MANGO: Disentangled Image Transformation Manifolds with Grouped Operators

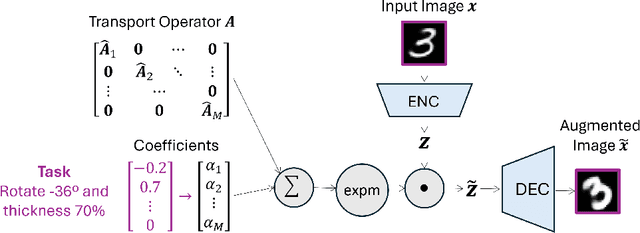
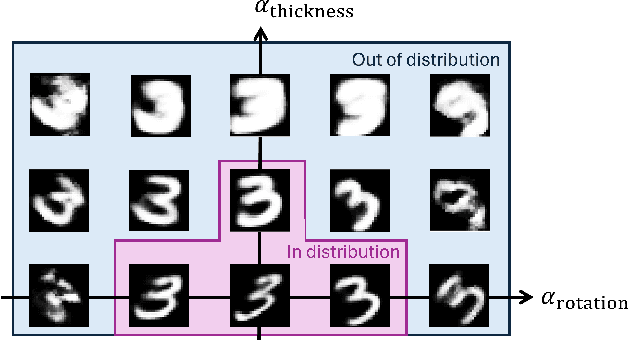
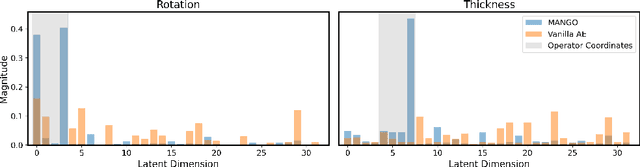
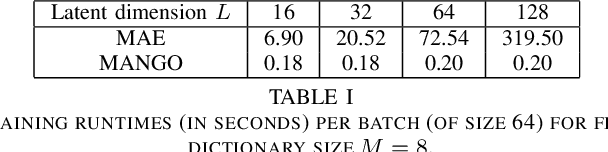
Learning semantically meaningful image transformations (i.e. rotation, thickness, blur) directly from examples can be a challenging task. Recently, the Manifold Autoencoder (MAE) proposed using a set of Lie group operators to learn image transformations directly from examples. However, this approach has limitations, as the learned operators are not guaranteed to be disentangled and the training routine is prohibitively expensive when scaling up the model. To address these limitations, we propose MANGO (transformation Manifolds with Grouped Operators) for learning disentangled operators that describe image transformations in distinct latent subspaces. Moreover, our approach allows practitioners the ability to define which transformations they aim to model, thus improving the semantic meaning of the learned operators. Through our experiments, we demonstrate that MANGO enables composition of image transformations and introduces a one-phase training routine that leads to a 100x speedup over prior works.

Precise asymptotics of reweighted least-squares algorithms for linear diagonal networks

The classical iteratively reweighted least-squares (IRLS) algorithm aims to recover an unknown signal from linear measurements by performing a sequence of weighted least squares problems, where the weights are recursively updated at each step. Varieties of this algorithm have been shown to achieve favorable empirical performance and theoretical guarantees for sparse recovery and $\ell_p$-norm minimization. Recently, some preliminary connections have also been made between IRLS and certain types of non-convex linear neural network architectures that are observed to exploit low-dimensional structure in high-dimensional linear models. In this work, we provide a unified asymptotic analysis for a family of algorithms that encompasses IRLS, the recently proposed lin-RFM algorithm (which was motivated by feature learning in neural networks), and the alternating minimization algorithm on linear diagonal neural networks. Our analysis operates in a "batched" setting with i.i.d. Gaussian covariates and shows that, with appropriately chosen reweighting policy, the algorithm can achieve favorable performance in only a handful of iterations. We also extend our results to the case of group-sparse recovery and show that leveraging this structure in the reweighting scheme provably improves test error compared to coordinate-wise reweighting.

Balanced Data, Imbalanced Spectra: Unveiling Class Disparities with Spectral Imbalance

Classification models are expected to perform equally well for different classes, yet in practice, there are often large gaps in their performance. This issue of class bias is widely studied in cases of datasets with sample imbalance, but is relatively overlooked in balanced datasets. In this work, we introduce the concept of spectral imbalance in features as a potential source for class disparities and study the connections between spectral imbalance and class bias in both theory and practice. To build the connection between spectral imbalance and class gap, we develop a theoretical framework for studying class disparities and derive exact expressions for the per-class error in a high-dimensional mixture model setting. We then study this phenomenon in 11 different state-of-the-art pretrained encoders and show how our proposed framework can be used to compare the quality of encoders, as well as evaluate and combine data augmentation strategies to mitigate the issue. Our work sheds light on the class-dependent effects of learning, and provides new insights into how state-of-the-art pretrained features may have unknown biases that can be diagnosed through their spectra.

New Equivalences Between Interpolation and SVMs: Kernels and Structured Features

The support vector machine (SVM) is a supervised learning algorithm that finds a maximum-margin linear classifier, often after mapping the data to a high-dimensional feature space via the kernel trick. Recent work has demonstrated that in certain sufficiently overparameterized settings, the SVM decision function coincides exactly with the minimum-norm label interpolant. This phenomenon of support vector proliferation (SVP) is especially interesting because it allows us to understand SVM performance by leveraging recent analyses of harmless interpolation in linear and kernel models. However, previous work on SVP has made restrictive assumptions on the data/feature distribution and spectrum. In this paper, we present a new and flexible analysis framework for proving SVP in an arbitrary reproducing kernel Hilbert space with a flexible class of generative models for the labels. We present conditions for SVP for features in the families of general bounded orthonormal systems (e.g. Fourier features) and independent sub-Gaussian features. In both cases, we show that SVP occurs in many interesting settings not covered by prior work, and we leverage these results to prove novel generalization results for kernel SVM classification.

The good, the bad and the ugly sides of data augmentation: An implicit spectral regularization perspective

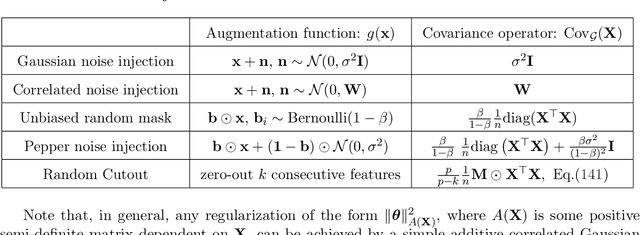
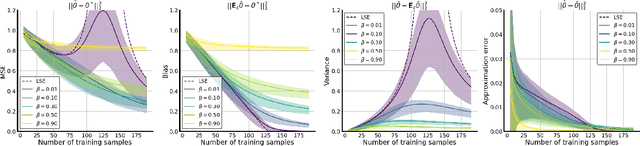
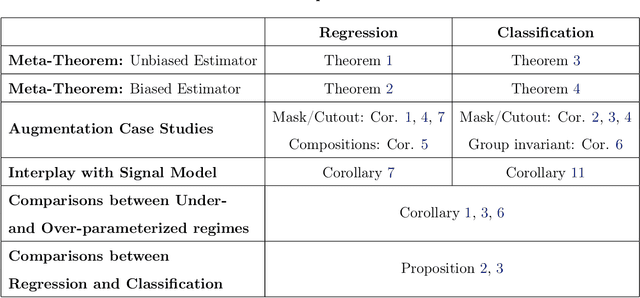
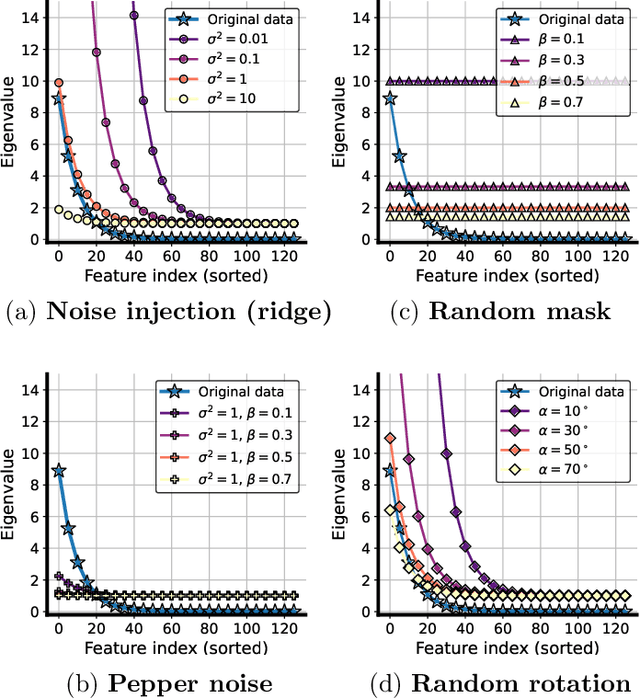
Data augmentation (DA) is a powerful workhorse for bolstering performance in modern machine learning. Specific augmentations like translations and scaling in computer vision are traditionally believed to improve generalization by generating new (artificial) data from the same distribution. However, this traditional viewpoint does not explain the success of prevalent augmentations in modern machine learning (e.g. randomized masking, cutout, mixup), that greatly alter the training data distribution. In this work, we develop a new theoretical framework to characterize the impact of a general class of DA on underparameterized and overparameterized linear model generalization. Our framework reveals that DA induces implicit spectral regularization through a combination of two distinct effects: a) manipulating the relative proportion of eigenvalues of the data covariance matrix in a training-data-dependent manner, and b) uniformly boosting the entire spectrum of the data covariance matrix through ridge regression. These effects, when applied to popular augmentations, give rise to a wide variety of phenomena, including discrepancies in generalization between over-parameterized and under-parameterized regimes and differences between regression and classification tasks. Our framework highlights the nuanced and sometimes surprising impacts of DA on generalization, and serves as a testbed for novel augmentation design.

Network topology change-point detection from graph signals with prior spectral signatures

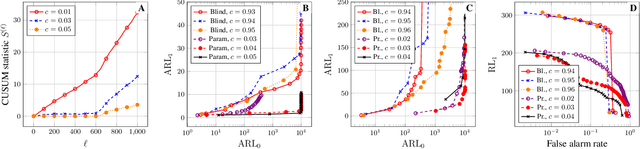
We consider the problem of sequential graph topology change-point detection from graph signals. We assume that signals on the nodes of the graph are regularized by the underlying graph structure via a graph filtering model, which we then leverage to distill the graph topology change-point detection problem to a subspace detection problem. We demonstrate how prior information on the spectral signature of the post-change graph can be incorporated to implicitly denoise the observed sequential data, thus leading to a natural CUSUM-based algorithm for change-point detection. Numerical experiments illustrate the performance of our proposed approach, particularly underscoring the benefits of (potentially noisy) prior information.