Stochastic Gradient Descent Jittering for Inverse Problems: Alleviating the Accuracy-Robustness Tradeoff

Inverse problems aim to reconstruct unseen data from corrupted or perturbed measurements. While most work focuses on improving reconstruction quality, generalization accuracy and robustness are equally important, especially for safety-critical applications. Model-based architectures (MBAs), such as loop unrolling methods, are considered more interpretable and achieve better reconstructions. Empirical evidence suggests that MBAs are more robust to perturbations than black-box solvers, but the accuracy-robustness tradeoff in MBAs remains underexplored. In this work, we propose a simple yet effective training scheme for MBAs, called SGD jittering, which injects noise iteration-wise during reconstruction. We theoretically demonstrate that SGD jittering not only generalizes better than the standard mean squared error training but is also more robust to average-case attacks. We validate SGD jittering using denoising toy examples, seismic deconvolution, and single-coil MRI reconstruction. The proposed method achieves cleaner reconstructions for out-of-distribution data and demonstrates enhanced robustness to adversarial attacks.

MANGO: Disentangled Image Transformation Manifolds with Grouped Operators

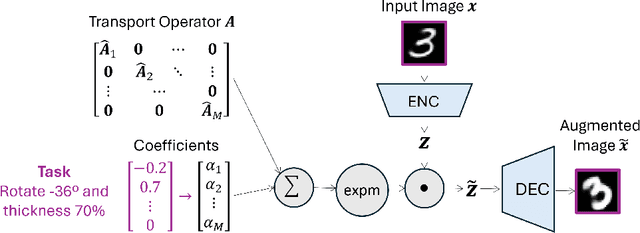
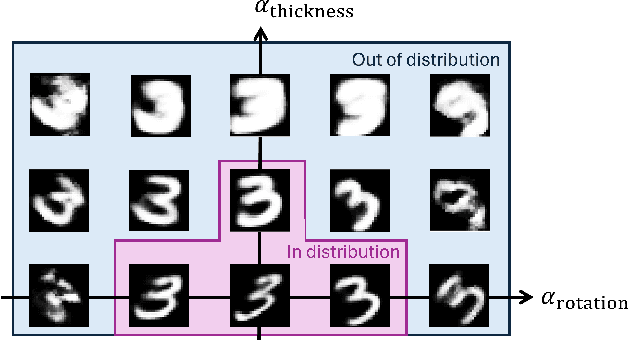
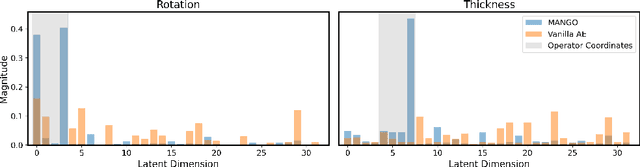
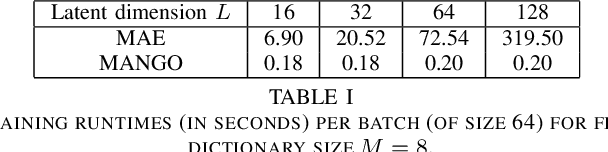
Learning semantically meaningful image transformations (i.e. rotation, thickness, blur) directly from examples can be a challenging task. Recently, the Manifold Autoencoder (MAE) proposed using a set of Lie group operators to learn image transformations directly from examples. However, this approach has limitations, as the learned operators are not guaranteed to be disentangled and the training routine is prohibitively expensive when scaling up the model. To address these limitations, we propose MANGO (transformation Manifolds with Grouped Operators) for learning disentangled operators that describe image transformations in distinct latent subspaces. Moreover, our approach allows practitioners the ability to define which transformations they aim to model, thus improving the semantic meaning of the learned operators. Through our experiments, we demonstrate that MANGO enables composition of image transformations and introduces a one-phase training routine that leads to a 100x speedup over prior works.

Solving Inverse Problems with Model Mismatch using Untrained Neural Networks within Model-based Architectures

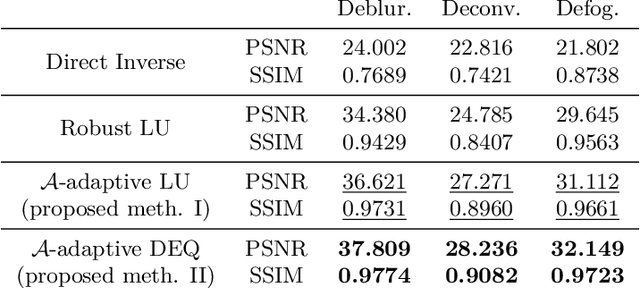
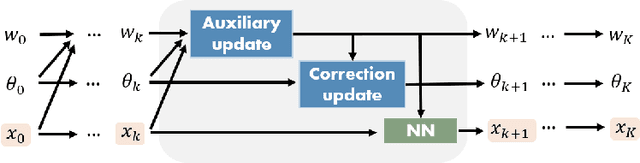
Model-based deep learning methods such as \emph{loop unrolling} (LU) and \emph{deep equilibrium model} (DEQ) extensions offer outstanding performance in solving inverse problems (IP). These methods unroll the optimization iterations into a sequence of neural networks that in effect learn a regularization function from data. While these architectures are currently state-of-the-art in numerous applications, their success heavily relies on the accuracy of the forward model. This assumption can be limiting in many physical applications due to model simplifications or uncertainties in the apparatus. To address forward model mismatch, we introduce an untrained forward model residual block within the model-based architecture to match the data consistency in the measurement domain for each instance. We propose two variants in well-known model-based architectures (LU and DEQ) and prove convergence under mild conditions. The experiments show significant quality improvement in removing artifacts and preserving details across three distinct applications, encompassing both linear and nonlinear inverse problems. Moreover, we highlight reconstruction effectiveness in intermediate steps and showcase robustness to random initialization of the residual block and a higher number of iterations during evaluation.

Learned Proximal Operator for Solving Seismic Deconvolution Problem

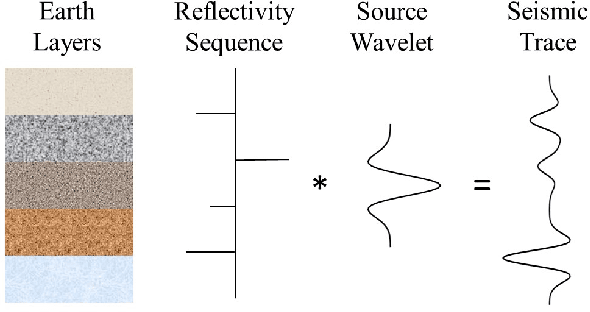
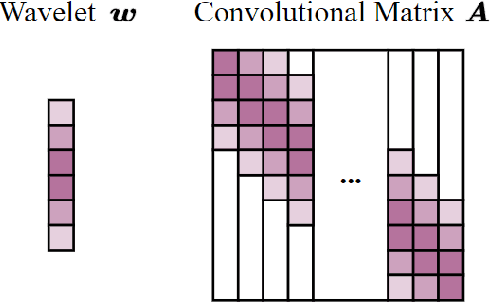
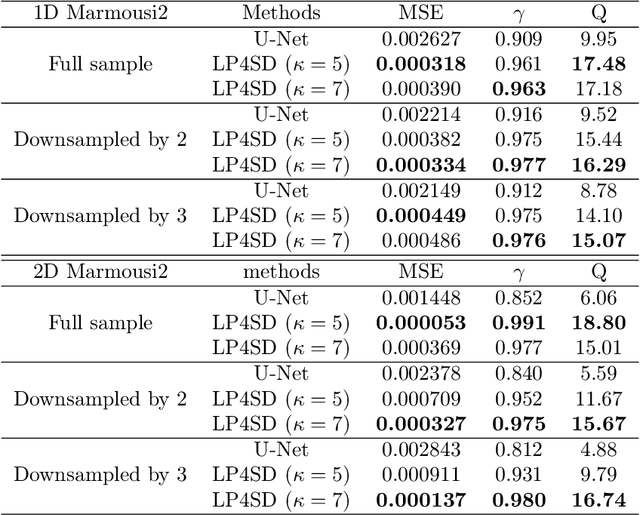
Seismic deconvolution is an essential step in seismic data processing that aims to extract layer information from noisy observed traces. In general, this is an ill-posed problem with non-unique solutions. Due to the sparse nature of the reflectivity sequence, spike-promoting regularizers such as the $\ell_1$-norm are frequently used. They either require rigorous coefficient tuning or strong assumptions about reflectivity, such as assuming reflectivity as sparse signals with known sparsity levels and zero-mean Gaussian noise with known noise levels. To overcome the limitations of traditional regularizers, learning-based regularizers are proposed in the recent past. This paper proposes a Learned Proximal operator for Seismic Deconvolution (LP4SD), which leverages a neural network to learn the proximal operator of a regularizer. LP4SD is trained in a loop unrolled manner and is capable of learning complicated structures from the training data. It is worth mentioning that the network is trained with synthetic data and evaluated on both synthetic and real data. LP4SD is shown to generate better reconstruction results in terms of three different metrics as compared to learning a direct inverse.

Loop Unrolled Shallow Equilibrium Regularizer (LUSER) -- A Memory-Efficient Inverse Problem Solver

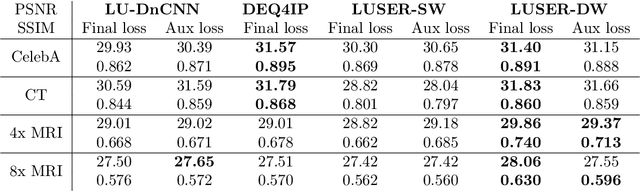
In inverse problems we aim to reconstruct some underlying signal of interest from potentially corrupted and often ill-posed measurements. Classical optimization-based techniques proceed by optimizing a data consistency metric together with a regularizer. Current state-of-the-art machine learning approaches draw inspiration from such techniques by unrolling the iterative updates for an optimization-based solver and then learning a regularizer from data. This loop unrolling (LU) method has shown tremendous success, but often requires a deep model for the best performance leading to high memory costs during training. Thus, to address the balance between computation cost and network expressiveness, we propose an LU algorithm with shallow equilibrium regularizers (LUSER). These implicit models are as expressive as deeper convolutional networks, but far more memory efficient during training. The proposed method is evaluated on image deblurring, computed tomography (CT), as well as single-coil Magnetic Resonance Imaging (MRI) tasks and shows similar, or even better, performance while requiring up to 8 times less computational resources during training when compared against a more typical LU architecture with feedforward convolutional regularizers.