MedVista3D: Vision-Language Modeling for Reducing Diagnostic Errors in 3D CT Disease Detection, Understanding and Reporting

Radiologic diagnostic errors-under-reading errors, inattentional blindness, and communication failures-remain prevalent in clinical practice. These issues often stem from missed localized abnormalities, limited global context, and variability in report language. These challenges are amplified in 3D imaging, where clinicians must examine hundreds of slices per scan. Addressing them requires systems with precise localized detection, global volume-level reasoning, and semantically consistent natural language reporting. However, existing 3D vision-language models are unable to meet all three needs jointly, lacking local-global understanding for spatial reasoning and struggling with the variability and noise of uncurated radiology reports. We present MedVista3D, a multi-scale semantic-enriched vision-language pretraining framework for 3D CT analysis. To enable joint disease detection and holistic interpretation, MedVista3D performs local and global image-text alignment for fine-grained representation learning within full-volume context. To address report variability, we apply language model rewrites and introduce a Radiology Semantic Matching Bank for semantics-aware alignment. MedVista3D achieves state-of-the-art performance on zero-shot disease classification, report retrieval, and medical visual question answering, while transferring well to organ segmentation and prognosis prediction. Code and datasets will be released.

MANGO: Disentangled Image Transformation Manifolds with Grouped Operators

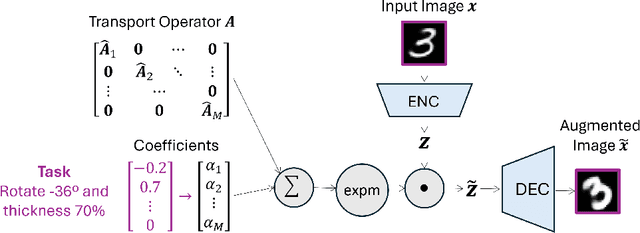
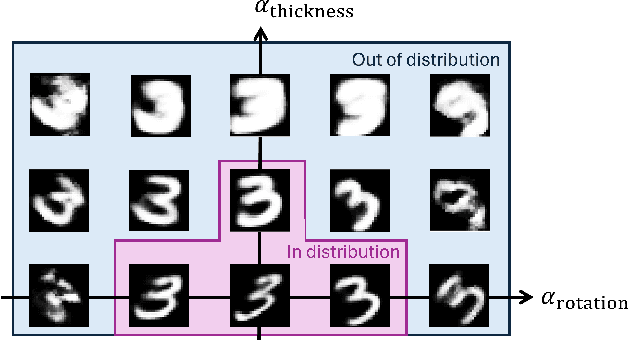
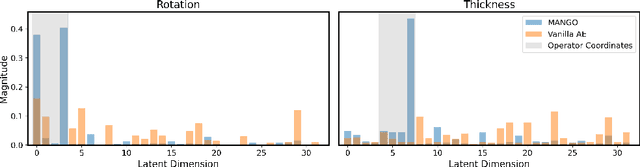
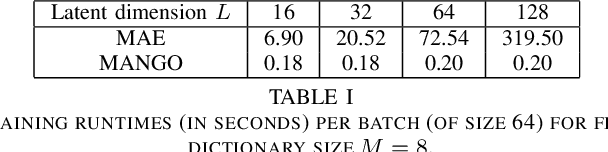
Learning semantically meaningful image transformations (i.e. rotation, thickness, blur) directly from examples can be a challenging task. Recently, the Manifold Autoencoder (MAE) proposed using a set of Lie group operators to learn image transformations directly from examples. However, this approach has limitations, as the learned operators are not guaranteed to be disentangled and the training routine is prohibitively expensive when scaling up the model. To address these limitations, we propose MANGO (transformation Manifolds with Grouped Operators) for learning disentangled operators that describe image transformations in distinct latent subspaces. Moreover, our approach allows practitioners the ability to define which transformations they aim to model, thus improving the semantic meaning of the learned operators. Through our experiments, we demonstrate that MANGO enables composition of image transformations and introduces a one-phase training routine that leads to a 100x speedup over prior works.

Probabilistic Decomposed Linear Dynamical Systems for Robust Discovery of Latent Neural Dynamics

Time-varying linear state-space models are powerful tools for obtaining mathematically interpretable representations of neural signals. For example, switching and decomposed models describe complex systems using latent variables that evolve according to simple locally linear dynamics. However, existing methods for latent variable estimation are not robust to dynamical noise and system nonlinearity due to noise-sensitive inference procedures and limited model formulations. This can lead to inconsistent results on signals with similar dynamics, limiting the model's ability to provide scientific insight. In this work, we address these limitations and propose a probabilistic approach to latent variable estimation in decomposed models that improves robustness against dynamical noise. Additionally, we introduce an extended latent dynamics model to improve robustness against system nonlinearities. We evaluate our approach on several synthetic dynamical systems, including an empirically-derived brain-computer interface experiment, and demonstrate more accurate latent variable inference in nonlinear systems with diverse noise conditions. Furthermore, we apply our method to a real-world clinical neurophysiology dataset, illustrating the ability to identify interpretable and coherent structure where previous models cannot.

AnatoMask: Enhancing Medical Image Segmentation with Reconstruction-guided Self-masking

Due to the scarcity of labeled data, self-supervised learning (SSL) has gained much attention in 3D medical image segmentation, by extracting semantic representations from unlabeled data. Among SSL strategies, Masked image modeling (MIM) has shown effectiveness by reconstructing randomly masked images to learn detailed representations. However, conventional MIM methods require extensive training data to achieve good performance, which still poses a challenge for medical imaging. Since random masking uniformly samples all regions within medical images, it may overlook crucial anatomical regions and thus degrade the pretraining efficiency. We propose AnatoMask, a novel MIM method that leverages reconstruction loss to dynamically identify and mask out anatomically significant regions to improve pretraining efficacy. AnatoMask takes a self-distillation approach, where the model learns both how to find more significant regions to mask and how to reconstruct these masked regions. To avoid suboptimal learning, Anatomask adjusts the pretraining difficulty progressively using a masking dynamics function. We have evaluated our method on 4 public datasets with multiple imaging modalities (CT, MRI, and PET). AnatoMask demonstrates superior performance and scalability compared to existing SSL methods. The code is available at https://github.com/ricklisz/AnatoMask.

LINOCS: Lookahead Inference of Networked Operators for Continuous Stability

Identifying latent interactions within complex systems is key to unlocking deeper insights into their operational dynamics, including how their elements affect each other and contribute to the overall system behavior. For instance, in neuroscience, discovering neuron-to-neuron interactions is essential for understanding brain function; in ecology, recognizing the interactions among populations is key for understanding complex ecosystems. Such systems, often modeled as dynamical systems, typically exhibit noisy high-dimensional and non-stationary temporal behavior that renders their identification challenging. Existing dynamical system identification methods often yield operators that accurately capture short-term behavior but fail to predict long-term trends, suggesting an incomplete capture of the underlying process. Methods that consider extended forecasts (e.g., recurrent neural networks) lack explicit representations of element-wise interactions and require substantial training data, thereby failing to capture interpretable network operators. Here we introduce Lookahead-driven Inference of Networked Operators for Continuous Stability (LINOCS), a robust learning procedure for identifying hidden dynamical interactions in noisy time-series data. LINOCS integrates several multi-step predictions with adaptive weights during training to recover dynamical operators that can yield accurate long-term predictions. We demonstrate LINOCS' ability to recover the ground truth dynamical operators underlying synthetic time-series data for multiple dynamical systems models (including linear, piece-wise linear, time-changing linear systems' decomposition, and regularized linear time-varying systems) as well as its capability to produce meaningful operators with robust reconstructions through various real-world examples.

Testing for context-dependent changes in neural encoding in naturalistic experiments

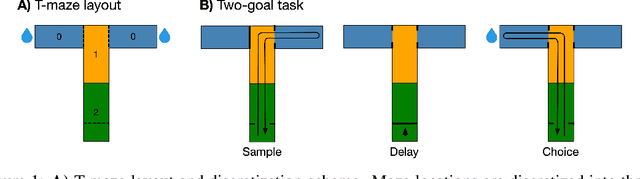
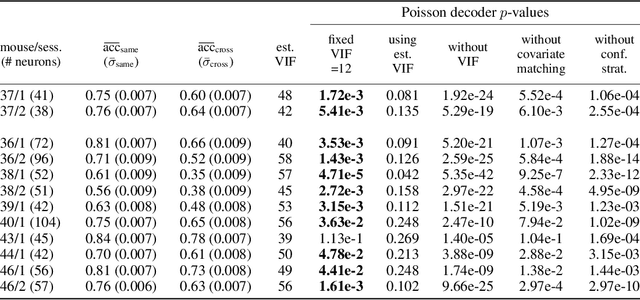
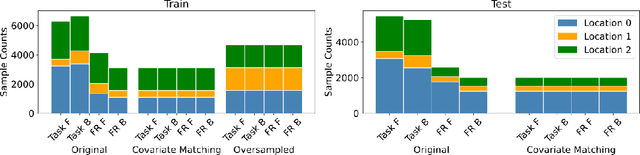
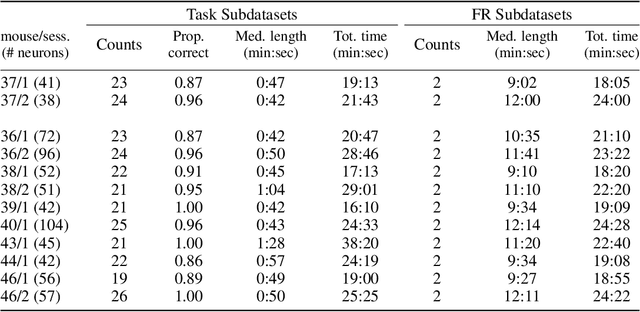
We propose a decoding-based approach to detect context effects on neural codes in longitudinal neural recording data. The approach is agnostic to how information is encoded in neural activity, and can control for a variety of possible confounding factors present in the data. We demonstrate our approach by determining whether it is possible to decode location encoding from prefrontal cortex in the mouse and, further, testing whether the encoding changes due to task engagement.

Decomposed Linear Dynamical Systems (dLDS) for learning the latent components of neural dynamics

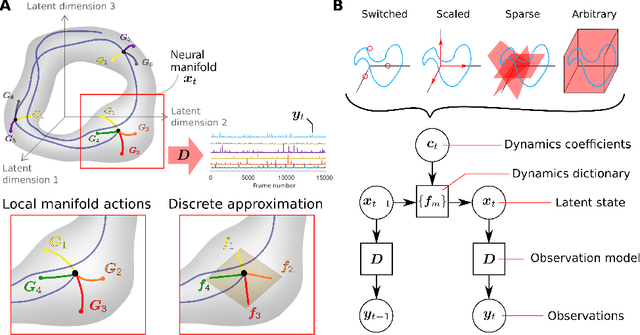
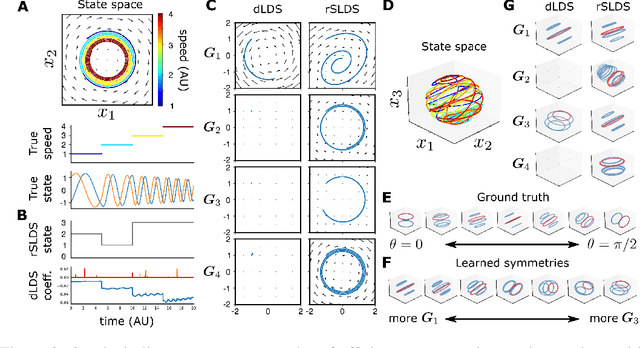
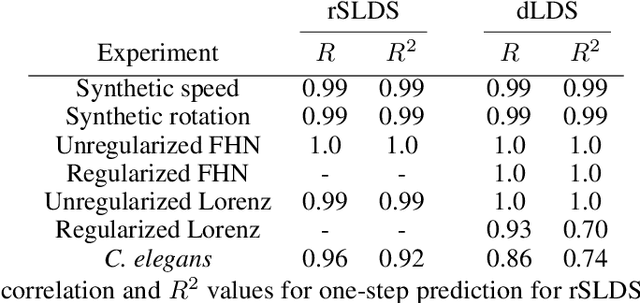
Learning interpretable representations of neural dynamics at a population level is a crucial first step to understanding how neural activity relates to perception and behavior. Models of neural dynamics often focus on either low-dimensional projections of neural activity, or on learning dynamical systems that explicitly relate to the neural state over time. We discuss how these two approaches are interrelated by considering dynamical systems as representative of flows on a low-dimensional manifold. Building on this concept, we propose a new decomposed dynamical system model that represents complex non-stationary and nonlinear dynamics of time-series data as a sparse combination of simpler, more interpretable components. The decomposed nature of the dynamics generalizes over previous switched approaches and enables modeling of overlapping and non-stationary drifts in the dynamics. We further present a dictionary learning-driven approach to model fitting, where we leverage recent results in tracking sparse vectors over time. We demonstrate that our model can learn efficient representations and smooth transitions between dynamical modes in both continuous-time and discrete-time examples. We show results on low-dimensional linear and nonlinear attractors to demonstrate that our decomposed dynamical systems model can well approximate nonlinear dynamics. Additionally, we apply our model to C. elegans data, illustrating a diversity of dynamics that is obscured when classified into discrete states.