Multiway Multislice PHATE: Visualizing Hidden Dynamics of RNNs through Training

Recurrent neural networks (RNNs) are a widely used tool for sequential data analysis, however, they are still often seen as black boxes of computation. Understanding the functional principles of these networks is critical to developing ideal model architectures and optimization strategies. Previous studies typically only emphasize the network representation post-training, overlooking their evolution process throughout training. Here, we present Multiway Multislice PHATE (MM-PHATE), a novel method for visualizing the evolution of RNNs' hidden states. MM-PHATE is a graph-based embedding using structured kernels across the multiple dimensions spanned by RNNs: time, training epoch, and units. We demonstrate on various datasets that MM-PHATE uniquely preserves hidden representation community structure among units and identifies information processing and compression phases during training. The embedding allows users to look under the hood of RNNs across training and provides an intuitive and comprehensive strategy to understanding the network's internal dynamics and draw conclusions, e.g., on why and how one model outperforms another or how a specific architecture might impact an RNN's learning ability.

LINOCS: Lookahead Inference of Networked Operators for Continuous Stability

Identifying latent interactions within complex systems is key to unlocking deeper insights into their operational dynamics, including how their elements affect each other and contribute to the overall system behavior. For instance, in neuroscience, discovering neuron-to-neuron interactions is essential for understanding brain function; in ecology, recognizing the interactions among populations is key for understanding complex ecosystems. Such systems, often modeled as dynamical systems, typically exhibit noisy high-dimensional and non-stationary temporal behavior that renders their identification challenging. Existing dynamical system identification methods often yield operators that accurately capture short-term behavior but fail to predict long-term trends, suggesting an incomplete capture of the underlying process. Methods that consider extended forecasts (e.g., recurrent neural networks) lack explicit representations of element-wise interactions and require substantial training data, thereby failing to capture interpretable network operators. Here we introduce Lookahead-driven Inference of Networked Operators for Continuous Stability (LINOCS), a robust learning procedure for identifying hidden dynamical interactions in noisy time-series data. LINOCS integrates several multi-step predictions with adaptive weights during training to recover dynamical operators that can yield accurate long-term predictions. We demonstrate LINOCS' ability to recover the ground truth dynamical operators underlying synthetic time-series data for multiple dynamical systems models (including linear, piece-wise linear, time-changing linear systems' decomposition, and regularized linear time-varying systems) as well as its capability to produce meaningful operators with robust reconstructions through various real-world examples.

Deep and shallow data science for multi-scale optical neuroscience

Optical imaging of the brain has expanded dramatically in the past two decades. New optics, indicators, and experimental paradigms are now enabling in-vivo imaging from the synaptic to the cortex-wide scales. To match the resulting flood of data across scales, computational methods are continuously being developed to meet the need of extracting biologically relevant information. In this pursuit, challenges arise in some domains (e.g., SNR and resolution limits in micron-scale data) that require specialized algorithms. These algorithms can, for example, make use of state-of-the-art machine learning to maximally learn the details of a given scale to optimize the processing pipeline. In contrast, other methods, however, such as graph signal processing, seek to abstract away from some of the details that are scale-specific to provide solutions to specific sub-problems common across scales of neuroimaging. Here we discuss limitations and tradeoffs in algorithmic design with the goal of identifying how data quality and variability can hamper algorithm use and dissemination.

Prospective Learning: Back to the Future

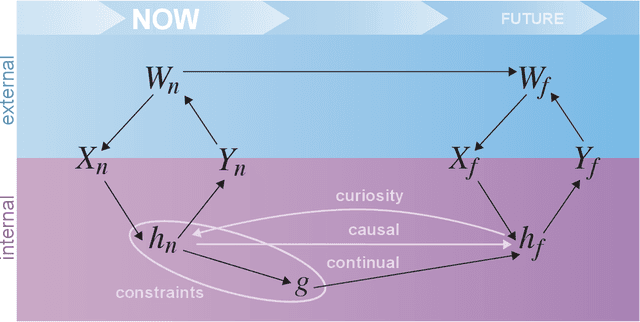
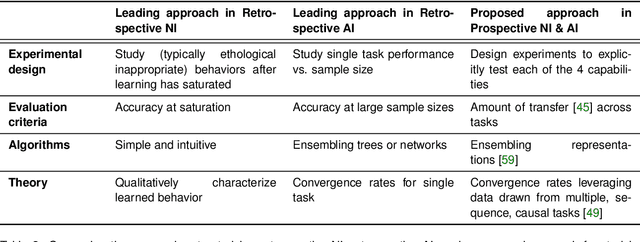
Research on both natural intelligence (NI) and artificial intelligence (AI) generally assumes that the future resembles the past: intelligent agents or systems (what we call 'intelligence') observe and act on the world, then use this experience to act on future experiences of the same kind. We call this 'retrospective learning'. For example, an intelligence may see a set of pictures of objects, along with their names, and learn to name them. A retrospective learning intelligence would merely be able to name more pictures of the same objects. We argue that this is not what true intelligence is about. In many real world problems, both NIs and AIs will have to learn for an uncertain future. Both must update their internal models to be useful for future tasks, such as naming fundamentally new objects and using these objects effectively in a new context or to achieve previously unencountered goals. This ability to learn for the future we call 'prospective learning'. We articulate four relevant factors that jointly define prospective learning. Continual learning enables intelligences to remember those aspects of the past which it believes will be most useful in the future. Prospective constraints (including biases and priors) facilitate the intelligence finding general solutions that will be applicable to future problems. Curiosity motivates taking actions that inform future decision making, including in previously unmet situations. Causal estimation enables learning the structure of relations that guide choosing actions for specific outcomes, even when the specific action-outcome contingencies have never been observed before. We argue that a paradigm shift from retrospective to prospective learning will enable the communities that study intelligence to unite and overcome existing bottlenecks to more effectively explain, augment, and engineer intelligences.

Matrix-normal models for fMRI analysis

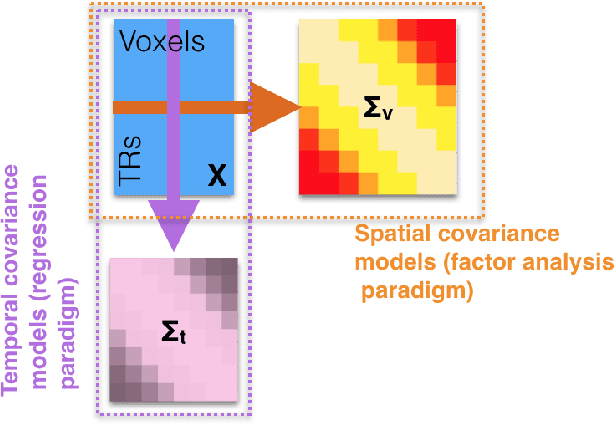
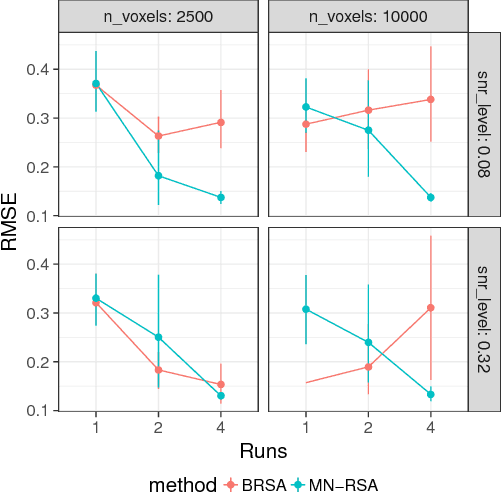
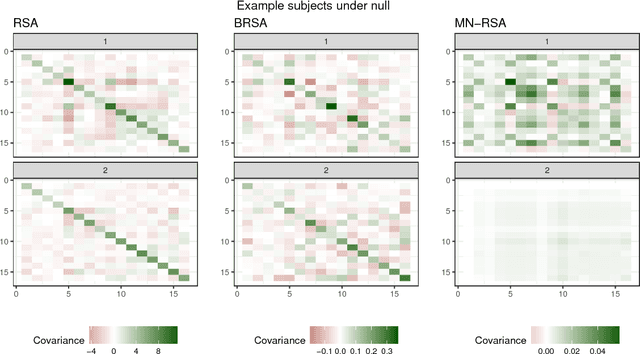
Multivariate analysis of fMRI data has benefited substantially from advances in machine learning. Most recently, a range of probabilistic latent variable models applied to fMRI data have been successful in a variety of tasks, including identifying similarity patterns in neural data (Representational Similarity Analysis and its empirical Bayes variant, RSA and BRSA; Intersubject Functional Connectivity, ISFC), combining multi-subject datasets (Shared Response Mapping; SRM), and mapping between brain and behavior (Joint Modeling). Although these methods share some underpinnings, they have been developed as distinct methods, with distinct algorithms and software tools. We show how the matrix-variate normal (MN) formalism can unify some of these methods into a single framework. In doing so, we gain the ability to reuse noise modeling assumptions, algorithms, and code across models. Our primary theoretical contribution shows how some of these methods can be written as instantiations of the same model, allowing us to generalize them to flexibly modeling structured noise covariances. Our formalism permits novel model variants and improved estimation strategies: in contrast to SRM, the number of parameters for MN-SRM does not scale with the number of voxels or subjects; in contrast to BRSA, the number of parameters for MN-RSA scales additively rather than multiplicatively in the number of voxels. We empirically demonstrate advantages of two new methods derived in the formalism: for MN-RSA, we show up to 10x improvement in runtime, up to 6x improvement in RMSE, and more conservative behavior under the null. For MN-SRM, our method grants a modest improvement to out-of-sample reconstruction while relaxing an orthonormality constraint of SRM. We also provide a software prototyping tool for MN models that can flexibly reuse noise covariance assumptions and algorithms across models.

Distributed Sequence Memory of Multidimensional Inputs in Recurrent Networks

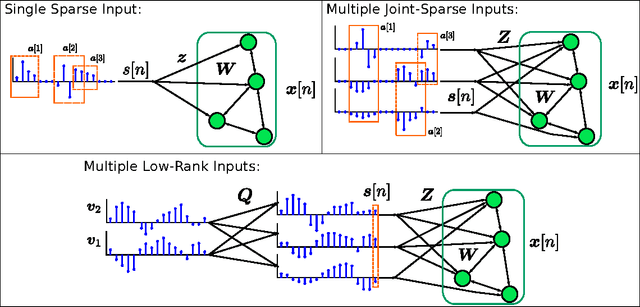
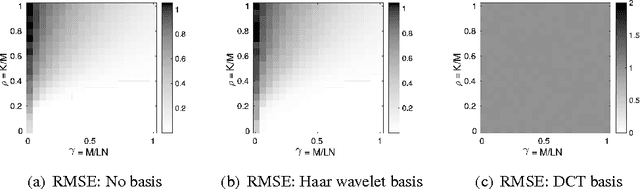
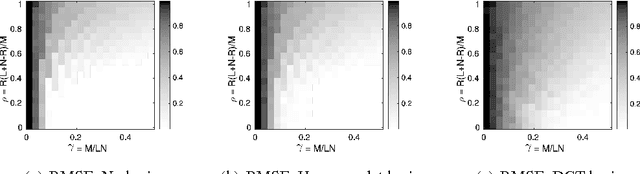
Recurrent neural networks (RNNs) have drawn interest from machine learning researchers because of their effectiveness at preserving past inputs for time-varying data processing tasks. To understand the success and limitations of RNNs, it is critical that we advance our analysis of their fundamental memory properties. We focus on echo state networks (ESNs), which are RNNs with simple memoryless nodes and random connectivity. In most existing analyses, the short-term memory (STM) capacity results conclude that the ESN network size must scale linearly with the input size for unstructured inputs. The main contribution of this paper is to provide general results characterizing the STM capacity for linear ESNs with multidimensional input streams when the inputs have common low-dimensional structure: sparsity in a basis or significant statistical dependence between inputs. In both cases, we show that the number of nodes in the network must scale linearly with the information rate and poly-logarithmically with the ambient input dimension. The analysis relies on advanced applications of random matrix theory and results in explicit non-asymptotic bounds on the recovery error. Taken together, this analysis provides a significant step forward in our understanding of the STM properties in RNNs.

Dynamic Filtering of Time-Varying Sparse Signals via l1 Minimization

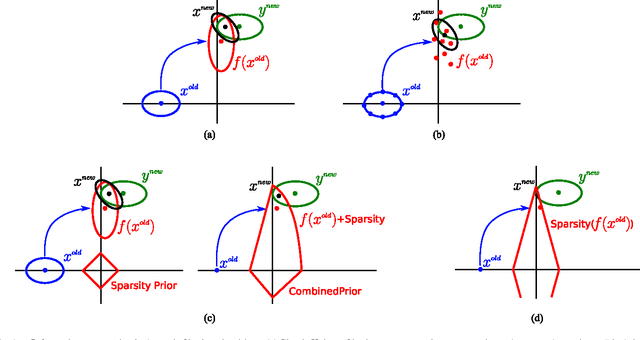
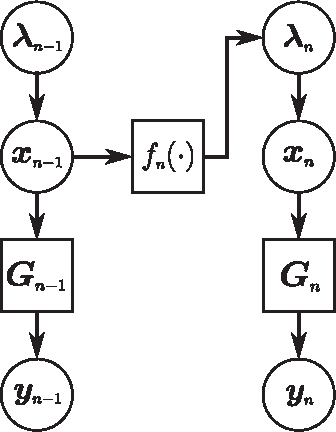
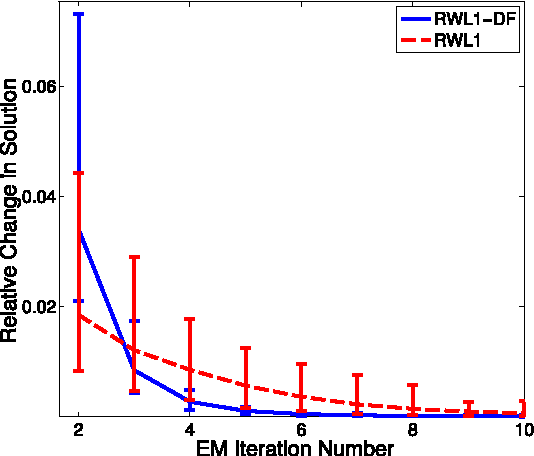
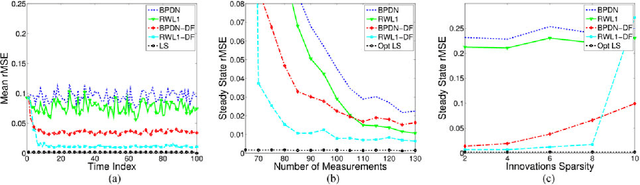
Despite the importance of sparsity signal models and the increasing prevalence of high-dimensional streaming data, there are relatively few algorithms for dynamic filtering of time-varying sparse signals. Of the existing algorithms, fewer still provide strong performance guarantees. This paper examines two algorithms for dynamic filtering of sparse signals that are based on efficient l1 optimization methods. We first present an analysis for one simple algorithm (BPDN-DF) that works well when the system dynamics are known exactly. We then introduce a novel second algorithm (RWL1-DF) that is more computationally complex than BPDN-DF but performs better in practice, especially in the case where the system dynamics model is inaccurate. Robustness to model inaccuracy is achieved by using a hierarchical probabilistic data model and propagating higher-order statistics from the previous estimate (akin to Kalman filtering) in the sparse inference process. We demonstrate the properties of these algorithms on both simulated data as well as natural video sequences. Taken together, the algorithms presented in this paper represent the first strong performance analysis of dynamic filtering algorithms for time-varying sparse signals as well as state-of-the-art performance in this emerging application.