Scaling and Distilling Transformer Models for sEMG

Surface electromyography (sEMG) signals offer a promising avenue for developing innovative human-computer interfaces by providing insights into muscular activity. However, the limited volume of training data and computational constraints during deployment have restricted the investigation of scaling up the model size for solving sEMG tasks. In this paper, we demonstrate that vanilla transformer models can be effectively scaled up on sEMG data and yield improved cross-user performance up to 110M parameters, surpassing the model size regime investigated in other sEMG research (usually <10M parameters). We show that >100M-parameter models can be effectively distilled into models 50x smaller with minimal loss of performance (<1.5% absolute). This results in efficient and expressive models suitable for complex real-time sEMG tasks in real-world environments.

AI Research Agents for Machine Learning: Search, Exploration, and Generalization in MLE-bench

AI research agents are demonstrating great potential to accelerate scientific progress by automating the design, implementation, and training of machine learning models. We focus on methods for improving agents' performance on MLE-bench, a challenging benchmark where agents compete in Kaggle competitions to solve real-world machine learning problems. We formalize AI research agents as search policies that navigate a space of candidate solutions, iteratively modifying them using operators. By designing and systematically varying different operator sets and search policies (Greedy, MCTS, Evolutionary), we show that their interplay is critical for achieving high performance. Our best pairing of search strategy and operator set achieves a state-of-the-art result on MLE-bench lite, increasing the success rate of achieving a Kaggle medal from 39.6% to 47.7%. Our investigation underscores the importance of jointly considering the search strategy, operator design, and evaluation methodology in advancing automated machine learning.

Response Time Improves Choice Prediction and Function Estimation for Gaussian Process Models of Perception and Preferences

Models for human choice prediction in preference learning and psychophysics often consider only binary response data, requiring many samples to accurately learn preferences or perceptual detection thresholds. The response time (RT) to make each choice captures additional information about the decision process, however existing models incorporating RTs for choice prediction do so in fully parametric settings or over discrete stimulus sets. This is in part because the de-facto standard model for choice RTs, the diffusion decision model (DDM), does not admit tractable, differentiable inference. The DDM thus cannot be easily integrated with flexible models for continuous, multivariate function approximation, particularly Gaussian process (GP) models. We propose a novel differentiable approximation to the DDM likelihood using a family of known, skewed three-parameter distributions. We then use this new likelihood to incorporate RTs into GP models for binary choices. Our RT-choice GPs enable both better latent value estimation and held-out choice prediction relative to baselines, which we demonstrate on three real-world multivariate datasets covering both human psychophysics and preference learning applications.

Look-Ahead Acquisition Functions for Bernoulli Level Set Estimation

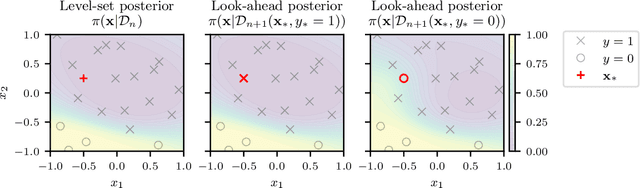
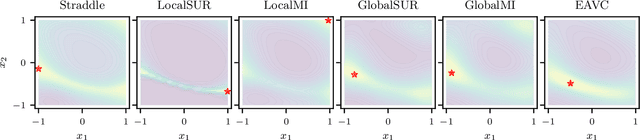
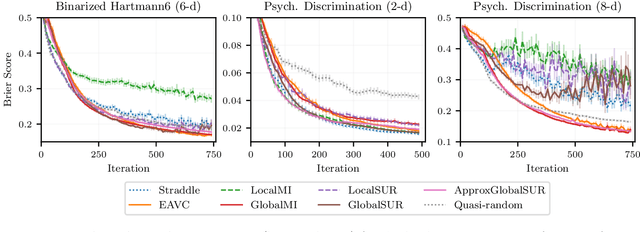
Level set estimation (LSE) is the problem of identifying regions where an unknown function takes values above or below a specified threshold. Active sampling strategies for efficient LSE have primarily been studied in continuous-valued functions. Motivated by applications in human psychophysics where common experimental designs produce binary responses, we study LSE active sampling with Bernoulli outcomes. With Gaussian process classification surrogate models, the look-ahead model posteriors used by state-of-the-art continuous-output methods are intractable. However, we derive analytic expressions for look-ahead posteriors of sublevel set membership, and show how these lead to analytic expressions for a class of look-ahead LSE acquisition functions, including information-based methods. Benchmark experiments show the importance of considering the global look-ahead impact on the entire posterior. We demonstrate a clear benefit to using this new class of acquisition functions on benchmark problems, and on a challenging real-world task of estimating a high-dimensional contrast sensitivity function.

Incorporating structured assumptions with probabilistic graphical models in fMRI data analysis

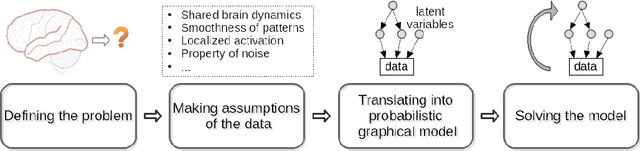
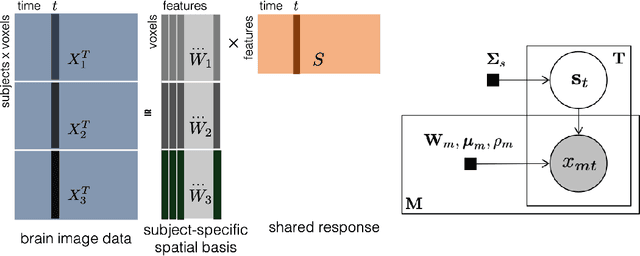
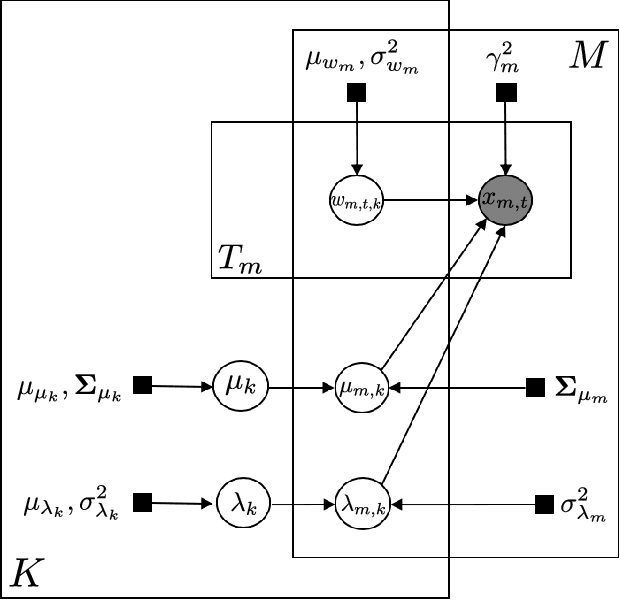
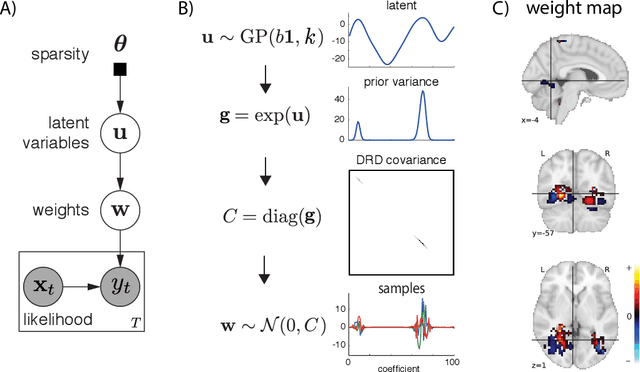
With the wide adoption of functional magnetic resonance imaging (fMRI) by cognitive neuroscience researchers, large volumes of brain imaging data have been accumulated in recent years. Aggregating these data to derive scientific insights often faces the challenge that fMRI data are high-dimensional, heterogeneous across people, and noisy. These challenges demand the development of computational tools that are tailored both for the neuroscience questions and for the properties of the data. We review a few recently developed algorithms in various domains of fMRI research: fMRI in naturalistic tasks, analyzing full-brain functional connectivity, pattern classification, inferring representational similarity and modeling structured residuals. These algorithms all tackle the challenges in fMRI similarly: they start by making clear statements of assumptions about neural data and existing domain knowledge, incorporating those assumptions and domain knowledge into probabilistic graphical models, and using those models to estimate properties of interest or latent structures in the data. Such approaches can avoid erroneous findings, reduce the impact of noise, better utilize known properties of the data, and better aggregate data across groups of subjects. With these successful cases, we advocate wider adoption of explicit model construction in cognitive neuroscience. Although we focus on fMRI, the principle illustrated here is generally applicable to brain data of other modalities.

Unifying Few- and Zero-Shot Egocentric Action Recognition

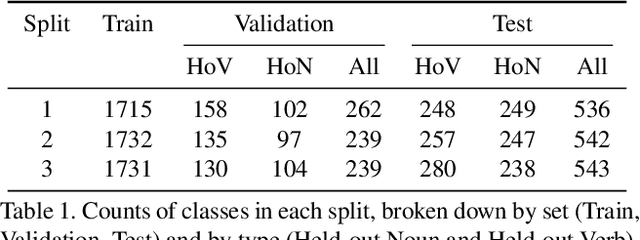
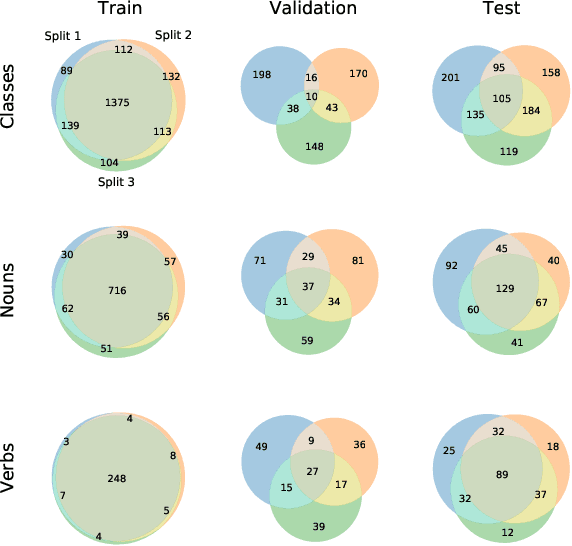
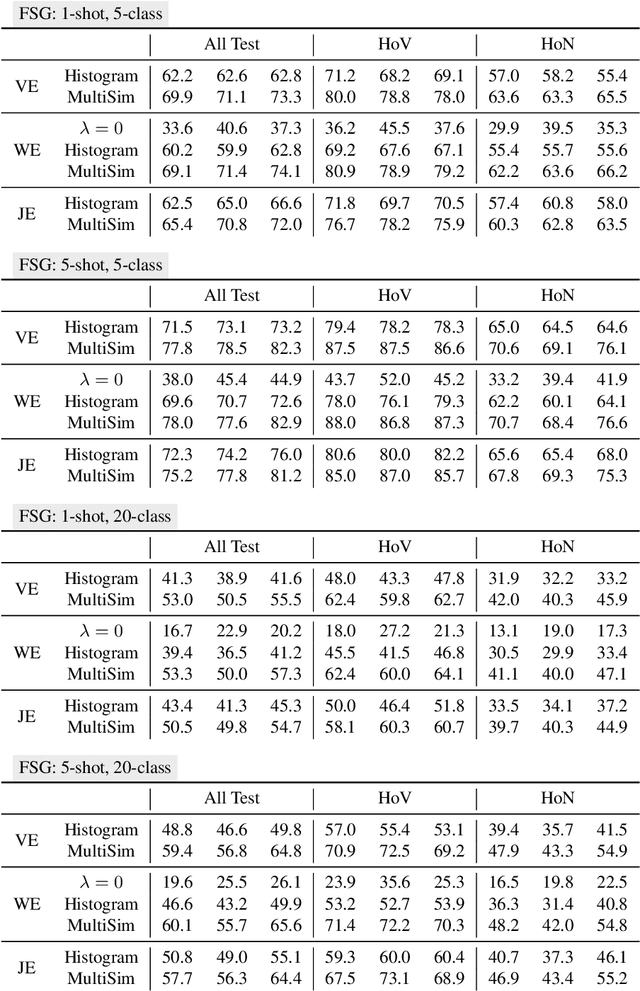
Although there has been significant research in egocentric action recognition, most methods and tasks, including EPIC-KITCHENS, suppose a fixed set of action classes. Fixed-set classification is useful for benchmarking methods, but is often unrealistic in practical settings due to the compositionality of actions, resulting in a functionally infinite-cardinality label set. In this work, we explore generalization with an open set of classes by unifying two popular approaches: few- and zero-shot generalization (the latter which we reframe as cross-modal few-shot generalization). We propose a new set of splits derived from the EPIC-KITCHENS dataset that allow evaluation of open-set classification, and use these splits to show that adding a metric-learning loss to the conventional direct-alignment baseline can improve zero-shot classification by as much as 10%, while not sacrificing few-shot performance.

Matrix-normal models for fMRI analysis

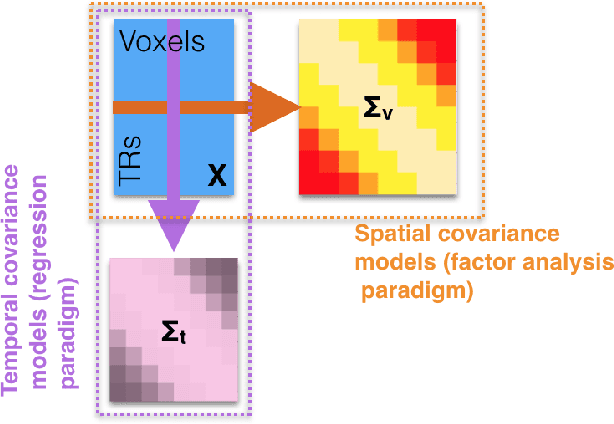
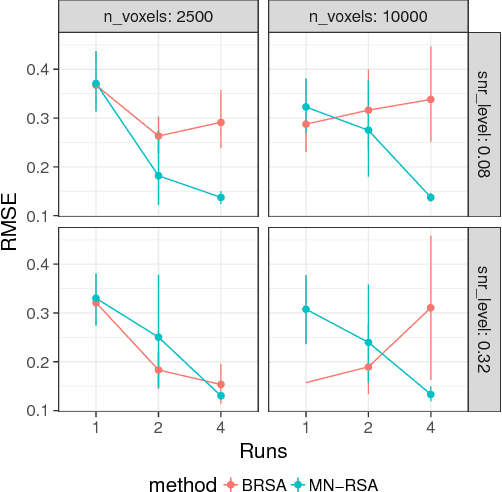
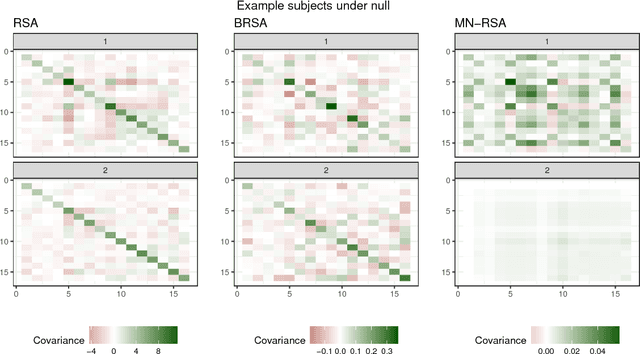
Multivariate analysis of fMRI data has benefited substantially from advances in machine learning. Most recently, a range of probabilistic latent variable models applied to fMRI data have been successful in a variety of tasks, including identifying similarity patterns in neural data (Representational Similarity Analysis and its empirical Bayes variant, RSA and BRSA; Intersubject Functional Connectivity, ISFC), combining multi-subject datasets (Shared Response Mapping; SRM), and mapping between brain and behavior (Joint Modeling). Although these methods share some underpinnings, they have been developed as distinct methods, with distinct algorithms and software tools. We show how the matrix-variate normal (MN) formalism can unify some of these methods into a single framework. In doing so, we gain the ability to reuse noise modeling assumptions, algorithms, and code across models. Our primary theoretical contribution shows how some of these methods can be written as instantiations of the same model, allowing us to generalize them to flexibly modeling structured noise covariances. Our formalism permits novel model variants and improved estimation strategies: in contrast to SRM, the number of parameters for MN-SRM does not scale with the number of voxels or subjects; in contrast to BRSA, the number of parameters for MN-RSA scales additively rather than multiplicatively in the number of voxels. We empirically demonstrate advantages of two new methods derived in the formalism: for MN-RSA, we show up to 10x improvement in runtime, up to 6x improvement in RMSE, and more conservative behavior under the null. For MN-SRM, our method grants a modest improvement to out-of-sample reconstruction while relaxing an orthonormality constraint of SRM. We also provide a software prototyping tool for MN models that can flexibly reuse noise covariance assumptions and algorithms across models.