Mixed Likelihood Variational Gaussian Processes

Gaussian processes (GPs) are powerful models for human-in-the-loop experiments due to their flexibility and well-calibrated uncertainty. However, GPs modeling human responses typically ignore auxiliary information, including a priori domain expertise and non-task performance information like user confidence ratings. We propose mixed likelihood variational GPs to leverage auxiliary information, which combine multiple likelihoods in a single evidence lower bound to model multiple types of data. We demonstrate the benefits of mixing likelihoods in three real-world experiments with human participants. First, we use mixed likelihood training to impose prior knowledge constraints in GP classifiers, which accelerates active learning in a visual perception task where users are asked to identify geometric errors resulting from camera position errors in virtual reality. Second, we show that leveraging Likert scale confidence ratings by mixed likelihood training improves model fitting for haptic perception of surface roughness. Lastly, we show that Likert scale confidence ratings improve human preference learning in robot gait optimization. The modeling performance improvements found using our framework across this diverse set of applications illustrates the benefits of incorporating auxiliary information into active learning and preference learning by using mixed likelihoods to jointly model multiple inputs.

Look-Ahead Acquisition Functions for Bernoulli Level Set Estimation

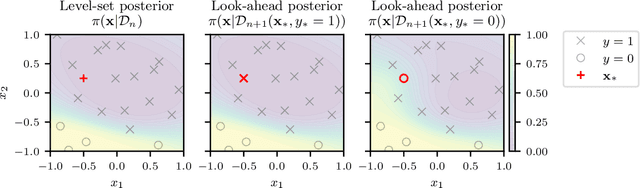
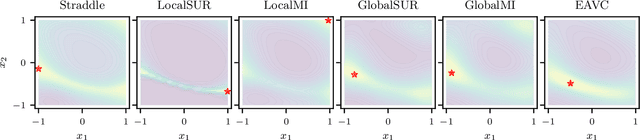
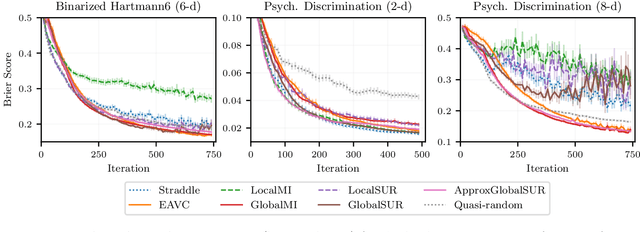
Level set estimation (LSE) is the problem of identifying regions where an unknown function takes values above or below a specified threshold. Active sampling strategies for efficient LSE have primarily been studied in continuous-valued functions. Motivated by applications in human psychophysics where common experimental designs produce binary responses, we study LSE active sampling with Bernoulli outcomes. With Gaussian process classification surrogate models, the look-ahead model posteriors used by state-of-the-art continuous-output methods are intractable. However, we derive analytic expressions for look-ahead posteriors of sublevel set membership, and show how these lead to analytic expressions for a class of look-ahead LSE acquisition functions, including information-based methods. Benchmark experiments show the importance of considering the global look-ahead impact on the entire posterior. We demonstrate a clear benefit to using this new class of acquisition functions on benchmark problems, and on a challenging real-world task of estimating a high-dimensional contrast sensitivity function.