Knowledge Gradient for Preference Learning

The knowledge gradient is a popular acquisition function in Bayesian optimization (BO) for optimizing black-box objectives with noisy function evaluations. Many practical settings, however, allow only pairwise comparison queries, yielding a preferential BO problem where direct function evaluations are unavailable. Extending the knowledge gradient to preferential BO is hindered by its computational challenge. At its core, the look-ahead step in the preferential setting requires computing a non-Gaussian posterior, which was previously considered intractable. In this paper, we address this challenge by deriving an exact and analytical knowledge gradient for preferential BO. We show that the exact knowledge gradient performs strongly on a suite of benchmark problems, often outperforming existing acquisition functions. In addition, we also present a case study illustrating the limitation of the knowledge gradient in certain scenarios.

Mixed Likelihood Variational Gaussian Processes

Gaussian processes (GPs) are powerful models for human-in-the-loop experiments due to their flexibility and well-calibrated uncertainty. However, GPs modeling human responses typically ignore auxiliary information, including a priori domain expertise and non-task performance information like user confidence ratings. We propose mixed likelihood variational GPs to leverage auxiliary information, which combine multiple likelihoods in a single evidence lower bound to model multiple types of data. We demonstrate the benefits of mixing likelihoods in three real-world experiments with human participants. First, we use mixed likelihood training to impose prior knowledge constraints in GP classifiers, which accelerates active learning in a visual perception task where users are asked to identify geometric errors resulting from camera position errors in virtual reality. Second, we show that leveraging Likert scale confidence ratings by mixed likelihood training improves model fitting for haptic perception of surface roughness. Lastly, we show that Likert scale confidence ratings improve human preference learning in robot gait optimization. The modeling performance improvements found using our framework across this diverse set of applications illustrates the benefits of incorporating auxiliary information into active learning and preference learning by using mixed likelihoods to jointly model multiple inputs.

Computation-Aware Gaussian Processes: Model Selection And Linear-Time Inference

Model selection in Gaussian processes scales prohibitively with the size of the training dataset, both in time and memory. While many approximations exist, all incur inevitable approximation error. Recent work accounts for this error in the form of computational uncertainty, which enables -- at the cost of quadratic complexity -- an explicit tradeoff between computation and precision. Here we extend this development to model selection, which requires significant enhancements to the existing approach, including linear-time scaling in the size of the dataset. We propose a novel training loss for hyperparameter optimization and demonstrate empirically that the resulting method can outperform SGPR, CGGP and SVGP, state-of-the-art methods for GP model selection, on medium to large-scale datasets. Our experiments show that model selection for computation-aware GPs trained on 1.8 million data points can be done within a few hours on a single GPU. As a result of this work, Gaussian processes can be trained on large-scale datasets without significantly compromising their ability to quantify uncertainty -- a fundamental prerequisite for optimal decision-making.

A Fast, Robust Elliptical Slice Sampling Implementation for Linearly Truncated Multivariate Normal Distributions

Elliptical slice sampling, when adapted to linearly truncated multivariate normal distributions, is a rejection-free Markov chain Monte Carlo method. At its core, it requires analytically constructing an ellipse-polytope intersection. The main novelty of this paper is an algorithm that computes this intersection in $\mathcal{O}(m \log m)$ time, where $m$ is the number of linear inequality constraints representing the polytope. We show that an implementation based on this algorithm enhances numerical stability, speeds up running time, and is easy to parallelize for launching multiple Markov chains.

Understanding Stochastic Natural Gradient Variational Inference

Stochastic natural gradient variational inference (NGVI) is a popular posterior inference method with applications in various probabilistic models. Despite its wide usage, little is known about the non-asymptotic convergence rate in the \emph{stochastic} setting. We aim to lessen this gap and provide a better understanding. For conjugate likelihoods, we prove the first $\mathcal{O}(\frac{1}{T})$ non-asymptotic convergence rate of stochastic NGVI. The complexity is no worse than stochastic gradient descent (\aka black-box variational inference) and the rate likely has better constant dependency that leads to faster convergence in practice. For non-conjugate likelihoods, we show that stochastic NGVI with the canonical parameterization implicitly optimizes a non-convex objective. Thus, a global convergence rate of $\mathcal{O}(\frac{1}{T})$ is unlikely without some significant new understanding of optimizing the ELBO using natural gradients.

Large-Scale Gaussian Processes via Alternating Projection

Gaussian process (GP) hyperparameter optimization requires repeatedly solving linear systems with $n \times n$ kernel matrices. To address the prohibitive $\mathcal{O}(n^3)$ time complexity, recent work has employed fast iterative numerical methods, like conjugate gradients (CG). However, as datasets increase in magnitude, the corresponding kernel matrices become increasingly ill-conditioned and still require $\mathcal{O}(n^2)$ space without partitioning. Thus, while CG increases the size of datasets GPs can be trained on, modern datasets reach scales beyond its applicability. In this work, we propose an iterative method which only accesses subblocks of the kernel matrix, effectively enabling \emph{mini-batching}. Our algorithm, based on alternating projection, has $\mathcal{O}(n)$ per-iteration time and space complexity, solving many of the practical challenges of scaling GPs to very large datasets. Theoretically, we prove our method enjoys linear convergence and empirically we demonstrate its robustness to ill-conditioning. On large-scale benchmark datasets up to four million datapoints our approach accelerates training by a factor of 2$\times$ to 27$\times$ compared to CG.

The Behavior and Convergence of Local Bayesian Optimization

A recent development in Bayesian optimization is the use of local optimization strategies, which can deliver strong empirical performance on high-dimensional problems compared to traditional global strategies. The "folk wisdom" in the literature is that the focus on local optimization sidesteps the curse of dimensionality; however, little is known concretely about the expected behavior or convergence of Bayesian local optimization routines. We first study the behavior of the local approach, and find that the statistics of individual local solutions of Gaussian process sample paths are surprisingly good compared to what we would expect to recover from global methods. We then present the first rigorous analysis of such a Bayesian local optimization algorithm recently proposed by M\"uller et al. (2021), and derive convergence rates in both the noisy and noiseless settings.

Black-Box Variational Inference Converges

We provide the first convergence guarantee for full black-box variational inference (BBVI), also known as Monte Carlo variational inference. While preliminary investigations worked on simplified versions of BBVI (e.g., bounded domain, bounded support, only optimizing for the scale, and such), our setup does not need any such algorithmic modifications. Our results hold for log-smooth posterior densities with and without strong log-concavity and the location-scale variational family. Also, our analysis reveals that certain algorithm design choices commonly employed in practice, particularly, nonlinear parameterizations of the scale of the variational approximation, can result in suboptimal convergence rates. Fortunately, running BBVI with proximal stochastic gradient descent fixes these limitations, and thus achieves the strongest known convergence rate guarantees. We evaluate this theoretical insight by comparing proximal SGD against other standard implementations of BBVI on large-scale Bayesian inference problems.

Practical and Matching Gradient Variance Bounds for Black-Box Variational Bayesian Inference

Understanding the gradient variance of black-box variational inference (BBVI) is a crucial step for establishing its convergence and developing algorithmic improvements. However, existing studies have yet to show that the gradient variance of BBVI satisfies the conditions used to study the convergence of stochastic gradient descent (SGD), the workhorse of BBVI. In this work, we show that BBVI satisfies a matching bound corresponding to the $ABC$ condition used in the SGD literature when applied to smooth and quadratically-growing log-likelihoods. Our results generalize to nonlinear covariance parameterizations widely used in the practice of BBVI. Furthermore, we show that the variance of the mean-field parameterization has provably superior dimensional dependence.

Stronger and Faster Wasserstein Adversarial Attacks

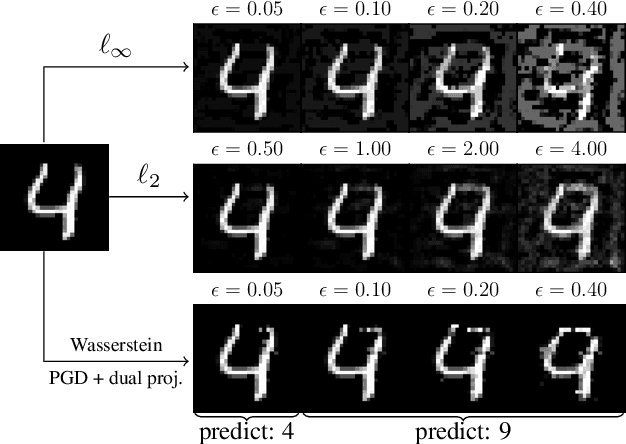
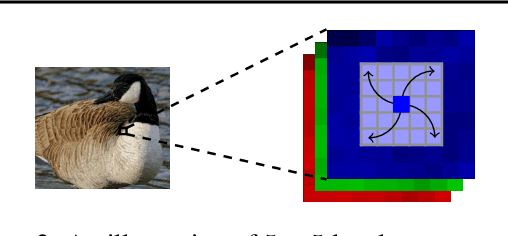
Deep models, while being extremely flexible and accurate, are surprisingly vulnerable to "small, imperceptible" perturbations known as adversarial attacks. While the majority of existing attacks focus on measuring perturbations under the $\ell_p$ metric, Wasserstein distance, which takes geometry in pixel space into account, has long been known to be a suitable metric for measuring image quality and has recently risen as a compelling alternative to the $\ell_p$ metric in adversarial attacks. However, constructing an effective attack under the Wasserstein metric is computationally much more challenging and calls for better optimization algorithms. We address this gap in two ways: (a) we develop an exact yet efficient projection operator to enable a stronger projected gradient attack; (b) we show that the Frank-Wolfe method equipped with a suitable linear minimization oracle works extremely fast under Wasserstein constraints. Our algorithms not only converge faster but also generate much stronger attacks. For instance, we decrease the accuracy of a residual network on CIFAR-10 to $3.4\%$ within a Wasserstein perturbation ball of radius $0.005$, in contrast to $65.6\%$ using the previous Wasserstein attack based on an \emph{approximate} projection operator. Furthermore, employing our stronger attacks in adversarial training significantly improves the robustness of adversarially trained models.