Mitigating Forgetting in Low Rank Adaptation

Parameter-efficient fine-tuning methods, such as Low-Rank Adaptation (LoRA), enable fast specialization of large pre-trained models to different downstream applications. However, this process often leads to catastrophic forgetting of the model's prior domain knowledge. We address this issue with LaLoRA, a weight-space regularization technique that applies a Laplace approximation to Low-Rank Adaptation. Our approach estimates the model's confidence in each parameter and constrains updates in high-curvature directions, preserving prior knowledge while enabling efficient target-domain learning. By applying the Laplace approximation only to the LoRA weights, the method remains lightweight. We evaluate LaLoRA by fine-tuning a Llama model for mathematical reasoning and demonstrate an improved learning-forgetting trade-off, which can be directly controlled via the method's regularization strength. We further explore different loss landscape curvature approximations for estimating parameter confidence, analyze the effect of the data used for the Laplace approximation, and study robustness across hyperparameters.

Closed-Form Last Layer Optimization

Neural networks are typically optimized with variants of stochastic gradient descent. Under a squared loss, however, the optimal solution to the linear last layer weights is known in closed-form. We propose to leverage this during optimization, treating the last layer as a function of the backbone parameters, and optimizing solely for these parameters. We show this is equivalent to alternating between gradient descent steps on the backbone and closed-form updates on the last layer. We adapt the method for the setting of stochastic gradient descent, by trading off the loss on the current batch against the accumulated information from previous batches. Further, we prove that, in the Neural Tangent Kernel regime, convergence of this method to an optimal solution is guaranteed. Finally, we demonstrate the effectiveness of our approach compared with standard SGD on a squared loss in several supervised tasks -- both regression and classification -- including Fourier Neural Operators and Instrumental Variable Regression.

laplax -- Laplace Approximations with JAX

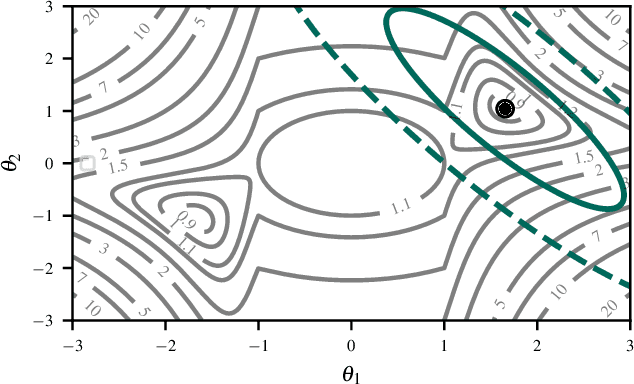
The Laplace approximation provides a scalable and efficient means of quantifying weight-space uncertainty in deep neural networks, enabling the application of Bayesian tools such as predictive uncertainty and model selection via Occam's razor. In this work, we introduce laplax, a new open-source Python package for performing Laplace approximations with jax. Designed with a modular and purely functional architecture and minimal external dependencies, laplax offers a flexible and researcher-friendly framework for rapid prototyping and experimentation. Its goal is to facilitate research on Bayesian neural networks, uncertainty quantification for deep learning, and the development of improved Laplace approximation techniques.

Connecting Parameter Magnitudes and Hessian Eigenspaces at Scale using Sketched Methods

Recently, it has been observed that when training a deep neural net with SGD, the majority of the loss landscape's curvature quickly concentrates in a tiny *top* eigenspace of the loss Hessian, which remains largely stable thereafter. Independently, it has been shown that successful magnitude pruning masks for deep neural nets emerge early in training and remain stable thereafter. In this work, we study these two phenomena jointly and show that they are connected: We develop a methodology to measure the similarity between arbitrary parameter masks and Hessian eigenspaces via Grassmannian metrics. We identify *overlap* as the most useful such metric due to its interpretability and stability. To compute *overlap*, we develop a matrix-free algorithm based on sketched SVDs that allows us to compute over 1000 Hessian eigenpairs for nets with over 10M parameters --an unprecedented scale by several orders of magnitude. Our experiments reveal an *overlap* between magnitude parameter masks and top Hessian eigenspaces consistently higher than chance-level, and that this effect gets accentuated for larger network sizes. This result indicates that *top Hessian eigenvectors tend to be concentrated around larger parameters*, or equivalently, that *larger parameters tend to align with directions of larger loss curvature*. Our work provides a methodology to approximate and analyze deep learning Hessians at scale, as well as a novel insight on the structure of their eigenspace.

Flexible and Efficient Probabilistic PDE Solvers through Gaussian Markov Random Fields

Mechanistic knowledge about the physical world is virtually always expressed via partial differential equations (PDEs). Recently, there has been a surge of interest in probabilistic PDE solvers -- Bayesian statistical models mostly based on Gaussian process (GP) priors which seamlessly combine empirical measurements and mechanistic knowledge. As such, they quantify uncertainties arising from e.g. noisy or missing data, unknown PDE parameters or discretization error by design. Prior work has established connections to classical PDE solvers and provided solid theoretical guarantees. However, scaling such methods to large-scale problems remains a fundamental challenge primarily due to dense covariance matrices. Our approach addresses the scalability issues by leveraging the Markov property of many commonly used GP priors. It has been shown that such priors are solutions to stochastic PDEs (SPDEs) which when discretized allow for highly efficient GP regression through sparse linear algebra. In this work, we show how to leverage this prior class to make probabilistic PDE solvers practical, even for large-scale nonlinear PDEs, through greatly accelerated inference mechanisms. Additionally, our approach also allows for flexible and physically meaningful priors beyond what can be modeled with covariance functions. Experiments confirm substantial speedups and accelerated convergence of our physics-informed priors in nonlinear settings.

Accelerating Neural Network Training: An Analysis of the AlgoPerf Competition

The goal of the AlgoPerf: Training Algorithms competition is to evaluate practical speed-ups in neural network training achieved solely by improving the underlying training algorithms. In the external tuning ruleset, submissions must provide workload-agnostic hyperparameter search spaces, while in the self-tuning ruleset they must be completely hyperparameter-free. In both rulesets, submissions are compared on time-to-result across multiple deep learning workloads, training on fixed hardware. This paper presents the inaugural AlgoPerf competition's results, which drew 18 diverse submissions from 10 teams. Our investigation reveals several key findings: (1) The winning submission in the external tuning ruleset, using Distributed Shampoo, demonstrates the effectiveness of non-diagonal preconditioning over popular methods like Adam, even when compared on wall-clock runtime. (2) The winning submission in the self-tuning ruleset, based on the Schedule Free AdamW algorithm, demonstrates a new level of effectiveness for completely hyperparameter-free training algorithms. (3) The top-scoring submissions were surprisingly robust to workload changes. We also discuss the engineering challenges encountered in ensuring a fair comparison between different training algorithms. These results highlight both the significant progress so far, and the considerable room for further improvements.

Rethinking Approximate Gaussian Inference in Classification

In classification tasks, softmax functions are ubiquitously used as output activations to produce predictive probabilities. Such outputs only capture aleatoric uncertainty. To capture epistemic uncertainty, approximate Gaussian inference methods have been proposed, which output Gaussian distributions over the logit space. Predictives are then obtained as the expectations of the Gaussian distributions pushed forward through the softmax. However, such softmax Gaussian integrals cannot be solved analytically, and Monte Carlo (MC) approximations can be costly and noisy. We propose a simple change in the learning objective which allows the exact computation of predictives and enjoys improved training dynamics, with no runtime or memory overhead. This framework is compatible with a family of output activation functions that includes the softmax, as well as element-wise normCDF and sigmoid. Moreover, it allows for approximating the Gaussian pushforwards with Dirichlet distributions by analytic moment matching. We evaluate our approach combined with several approximate Gaussian inference methods (Laplace, HET, SNGP) on large- and small-scale datasets (ImageNet, CIFAR-10), demonstrating improved uncertainty quantification capabilities compared to softmax MC sampling. Code is available at https://github.com/bmucsanyi/probit.

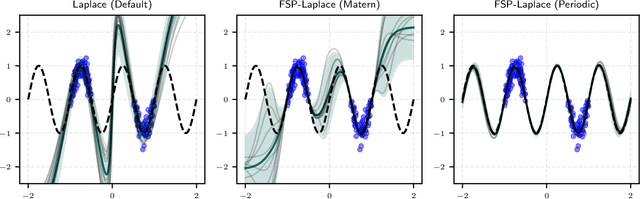
Learning convolution operators on compact Abelian groups

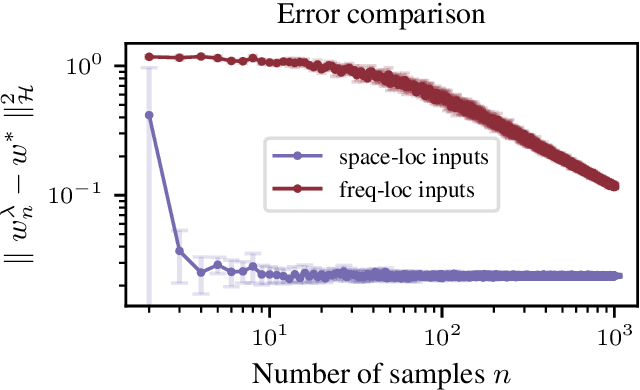
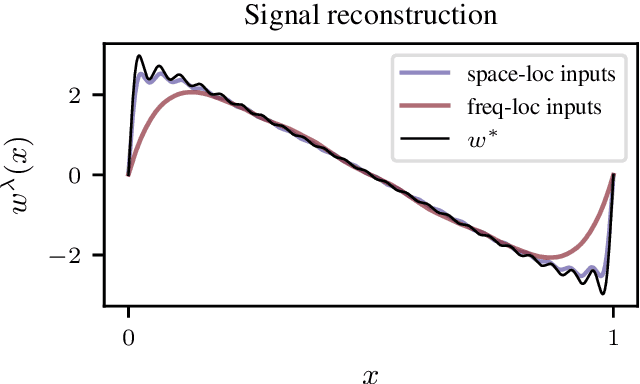
We consider the problem of learning convolution operators associated to compact Abelian groups. We study a regularization-based approach and provide corresponding learning guarantees, discussing natural regularity condition on the convolution kernel. More precisely, we assume the convolution kernel is a function in a translation invariant Hilbert space and analyze a natural ridge regression (RR) estimator. Building on existing results for RR, we characterize the accuracy of the estimator in terms of finite sample bounds. Interestingly, regularity assumptions which are classical in the analysis of RR, have a novel and natural interpretation in terms of space/frequency localization. Theoretical results are illustrated by numerical simulations.

Spatiotemporally Coherent Probabilistic Generation of Weather from Climate

Local climate information is crucial for impact assessment and decision-making, yet coarse global climate simulations cannot capture small-scale phenomena. Current statistical downscaling methods infer these phenomena as temporally decoupled spatial patches. However, to preserve physical properties, estimating spatio-temporally coherent high-resolution weather dynamics for multiple variables across long time horizons is crucial. We present a novel generative approach that uses a score-based diffusion model trained on high-resolution reanalysis data to capture the statistical properties of local weather dynamics. After training, we condition on coarse climate model data to generate weather patterns consistent with the aggregate information. As this inference task is inherently uncertain, we leverage the probabilistic nature of diffusion models and sample multiple trajectories. We evaluate our approach with high-resolution reanalysis information before applying it to the climate model downscaling task. We then demonstrate that the model generates spatially and temporally coherent weather dynamics that align with global climate output.

Computation-Aware Gaussian Processes: Model Selection And Linear-Time Inference

Model selection in Gaussian processes scales prohibitively with the size of the training dataset, both in time and memory. While many approximations exist, all incur inevitable approximation error. Recent work accounts for this error in the form of computational uncertainty, which enables -- at the cost of quadratic complexity -- an explicit tradeoff between computation and precision. Here we extend this development to model selection, which requires significant enhancements to the existing approach, including linear-time scaling in the size of the dataset. We propose a novel training loss for hyperparameter optimization and demonstrate empirically that the resulting method can outperform SGPR, CGGP and SVGP, state-of-the-art methods for GP model selection, on medium to large-scale datasets. Our experiments show that model selection for computation-aware GPs trained on 1.8 million data points can be done within a few hours on a single GPU. As a result of this work, Gaussian processes can be trained on large-scale datasets without significantly compromising their ability to quantify uncertainty -- a fundamental prerequisite for optimal decision-making.