Position: Curvature Matrices Should Be Democratized via Linear Operators

Structured large matrices are prevalent in machine learning. A particularly important class is curvature matrices like the Hessian, which are central to understanding the loss landscape of neural nets (NNs), and enable second-order optimization, uncertainty quantification, model pruning, data attribution, and more. However, curvature computations can be challenging due to the complexity of automatic differentiation, and the variety and structural assumptions of curvature proxies, like sparsity and Kronecker factorization. In this position paper, we argue that linear operators -- an interface for performing matrix-vector products -- provide a general, scalable, and user-friendly abstraction to handle curvature matrices. To support this position, we developed $\textit{curvlinops}$, a library that provides curvature matrices through a unified linear operator interface. We demonstrate with $\textit{curvlinops}$ how this interface can hide complexity, simplify applications, be extensible and interoperable with other libraries, and scale to large NNs.

Debiasing Mini-Batch Quadratics for Applications in Deep Learning

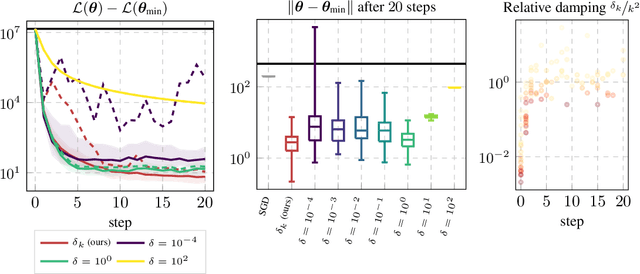
Quadratic approximations form a fundamental building block of machine learning methods. E.g., second-order optimizers try to find the Newton step into the minimum of a local quadratic proxy to the objective function; and the second-order approximation of a network's loss function can be used to quantify the uncertainty of its outputs via the Laplace approximation. When computations on the entire training set are intractable - typical for deep learning - the relevant quantities are computed on mini-batches. This, however, distorts and biases the shape of the associated stochastic quadratic approximations in an intricate way with detrimental effects on applications. In this paper, we (i) show that this bias introduces a systematic error, (ii) provide a theoretical explanation for it, (iii) explain its relevance for second-order optimization and uncertainty quantification via the Laplace approximation in deep learning, and (iv) develop and evaluate debiasing strategies.

Reparameterization invariance in approximate Bayesian inference

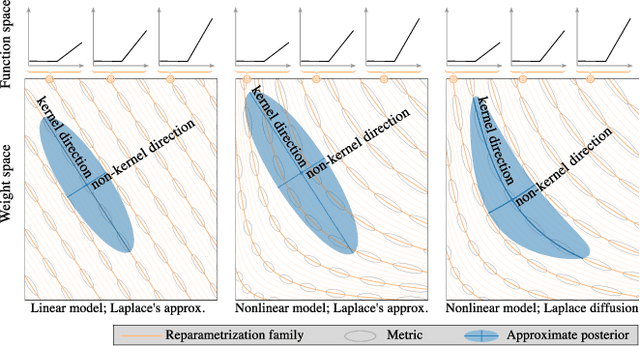
Current approximate posteriors in Bayesian neural networks (BNNs) exhibit a crucial limitation: they fail to maintain invariance under reparameterization, i.e. BNNs assign different posterior densities to different parametrizations of identical functions. This creates a fundamental flaw in the application of Bayesian principles as it breaks the correspondence between uncertainty over the parameters with uncertainty over the parametrized function. In this paper, we investigate this issue in the context of the increasingly popular linearized Laplace approximation. Specifically, it has been observed that linearized predictives alleviate the common underfitting problems of the Laplace approximation. We develop a new geometric view of reparametrizations from which we explain the success of linearization. Moreover, we demonstrate that these reparameterization invariance properties can be extended to the original neural network predictive using a Riemannian diffusion process giving a straightforward algorithm for approximate posterior sampling, which empirically improves posterior fit.

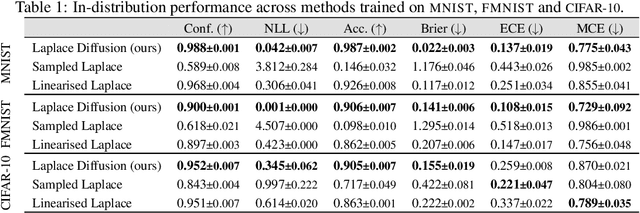
Accelerating Generalized Linear Models by Trading off Computation for Uncertainty

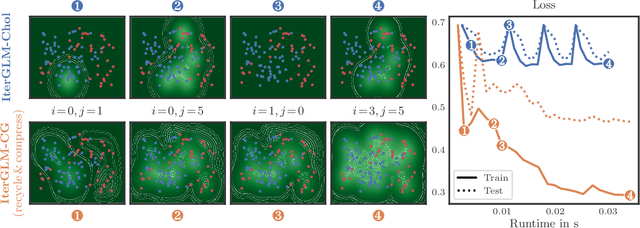
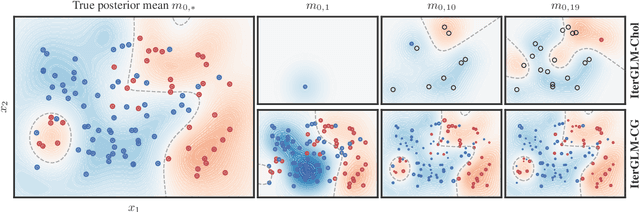
Bayesian Generalized Linear Models (GLMs) define a flexible probabilistic framework to model categorical, ordinal and continuous data, and are widely used in practice. However, exact inference in GLMs is prohibitively expensive for large datasets, thus requiring approximations in practice. The resulting approximation error adversely impacts the reliability of the model and is not accounted for in the uncertainty of the prediction. In this work, we introduce a family of iterative methods that explicitly model this error. They are uniquely suited to parallel modern computing hardware, efficiently recycle computations, and compress information to reduce both the time and memory requirements for GLMs. As we demonstrate on a realistically large classification problem, our method significantly accelerates training by explicitly trading off reduced computation for increased uncertainty.

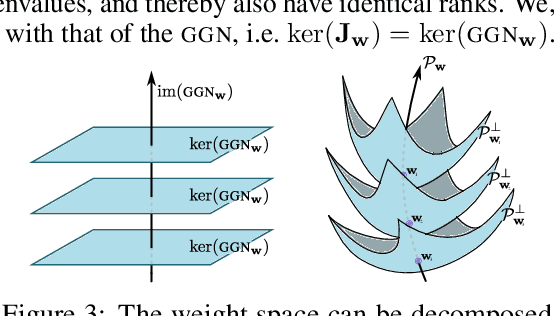
ViViT: Curvature access through the generalized Gauss-Newton's low-rank structure

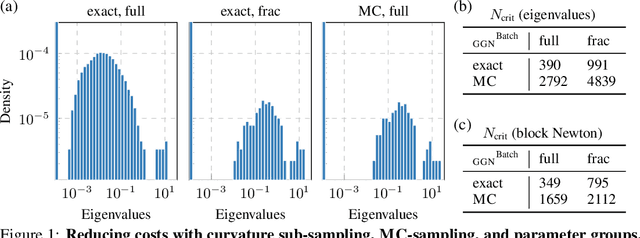
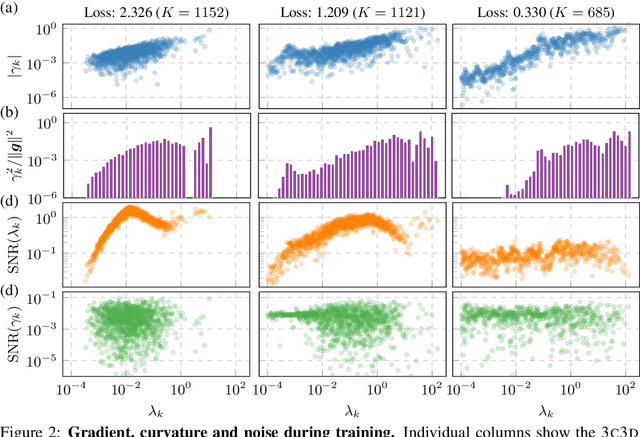
Curvature in form of the Hessian or its generalized Gauss-Newton (GGN) approximation is valuable for algorithms that rely on a local model for the loss to train, compress, or explain deep networks. Existing methods based on implicit multiplication via automatic differentiation or Kronecker-factored block diagonal approximations do not consider noise in the mini-batch. We present ViViT, a curvature model that leverages the GGN's low-rank structure without further approximations. It allows for efficient computation of eigenvalues, eigenvectors, as well as per-sample first- and second-order directional derivatives. The representation is computed in parallel with gradients in one backward pass and offers a fine-grained cost-accuracy trade-off, which allows it to scale. As examples for ViViT's usefulness, we investigate the directional gradients and curvatures during training, and how noise information can be used to improve the stability of second-order methods.