Simplifying Bayesian Optimization Via In-Context Direct Optimum Sampling

The optimization of expensive black-box functions is ubiquitous in science and engineering. A common solution to this problem is Bayesian optimization (BO), which is generally comprised of two components: (i) a surrogate model and (ii) an acquisition function, which generally require expensive re-training and optimization steps at each iteration, respectively. Although recent work enabled in-context surrogate models that do not require re-training, virtually all existing BO methods still require acquisition function maximization to select the next observation, which introduces many knobs to tune, such as Monte Carlo samplers and multi-start optimizers. In this work, we propose a completely in-context, zero-shot solution for BO that does not require surrogate fitting or acquisition function optimization. This is done by using a pre-trained deep generative model to directly sample from the posterior over the optimum point. We show that this process is equivalent to Thompson sampling and demonstrate the capabilities and cost-effectiveness of our foundation model on a suite of real-world benchmarks. We achieve an efficiency gain of more than 35x in terms of wall-clock time when compared with Gaussian process-based BO, enabling efficient parallel and distributed BO, e.g., for high-throughput optimization.

FlashMD: long-stride, universal prediction of molecular dynamics

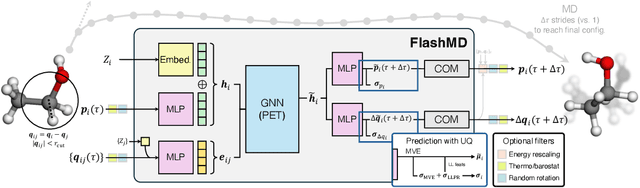
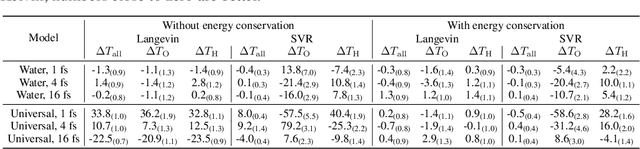
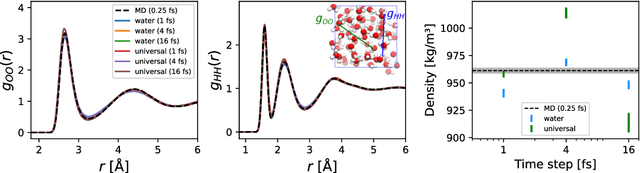
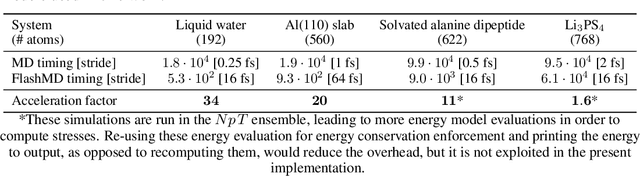
Molecular dynamics (MD) provides insights into atomic-scale processes by integrating over time the equations that describe the motion of atoms under the action of interatomic forces. Machine learning models have substantially accelerated MD by providing inexpensive predictions of the forces, but they remain constrained to minuscule time integration steps, which are required by the fast time scale of atomic motion. In this work, we propose FlashMD, a method to predict the evolution of positions and momenta over strides that are between one and two orders of magnitude longer than typical MD time steps. We incorporate considerations on the mathematical and physical properties of Hamiltonian dynamics in the architecture, generalize the approach to allow the simulation of any thermodynamic ensemble, and carefully assess the possible failure modes of such a long-stride MD approach. We validate FlashMD's accuracy in reproducing equilibrium and time-dependent properties, using both system-specific and general-purpose models, extending the ability of MD simulation to reach the long time scales needed to model microscopic processes of high scientific and technological relevance.

One Set to Rule Them All: How to Obtain General Chemical Conditions via Bayesian Optimization over Curried Functions

General parameters are highly desirable in the natural sciences - e.g., chemical reaction conditions that enable high yields across a range of related transformations. This has a significant practical impact since those general parameters can be transferred to related tasks without the need for laborious and time-intensive re-optimization. While Bayesian optimization (BO) is widely applied to find optimal parameter sets for specific tasks, it has remained underused in experiment planning towards such general optima. In this work, we consider the real-world problem of condition optimization for chemical reactions to study how performing generality-oriented BO can accelerate the identification of general optima, and whether these optima also translate to unseen examples. This is achieved through a careful formulation of the problem as an optimization over curried functions, as well as systematic evaluations of generality-oriented strategies for optimization tasks on real-world experimental data. We find that for generality-oriented optimization, simple myopic optimization strategies that decouple parameter and task selection perform comparably to more complex ones, and that effective optimization is merely determined by an effective exploration of both parameter and task space.

Towards Cost-Effective Reward Guided Text Generation

Reward-guided text generation (RGTG) has emerged as a viable alternative to offline reinforcement learning from human feedback (RLHF). RGTG methods can align baseline language models to human preferences without further training like in standard RLHF methods. However, they rely on a reward model to score each candidate token generated by the language model at inference, incurring significant test-time overhead. Additionally, the reward model is usually only trained to score full sequences, which can lead to sub-optimal choices for partial sequences. In this work, we present a novel reward model architecture that is trained, using a Bradley-Terry loss, to prefer the optimal expansion of a sequence with just a \emph{single call} to the reward model at each step of the generation process. That is, a score for all possible candidate tokens is generated simultaneously, leading to efficient inference. We theoretically analyze various RGTG reward models and demonstrate that prior techniques prefer sub-optimal sequences compared to our method during inference. Empirically, our reward model leads to significantly faster inference than other RGTG methods. It requires fewer calls to the reward model and performs competitively compared to previous RGTG and offline RLHF methods.

Position: Curvature Matrices Should Be Democratized via Linear Operators

Structured large matrices are prevalent in machine learning. A particularly important class is curvature matrices like the Hessian, which are central to understanding the loss landscape of neural nets (NNs), and enable second-order optimization, uncertainty quantification, model pruning, data attribution, and more. However, curvature computations can be challenging due to the complexity of automatic differentiation, and the variety and structural assumptions of curvature proxies, like sparsity and Kronecker factorization. In this position paper, we argue that linear operators -- an interface for performing matrix-vector products -- provide a general, scalable, and user-friendly abstraction to handle curvature matrices. To support this position, we developed $\textit{curvlinops}$, a library that provides curvature matrices through a unified linear operator interface. We demonstrate with $\textit{curvlinops}$ how this interface can hide complexity, simplify applications, be extensible and interoperable with other libraries, and scale to large NNs.

Efficient Weight-Space Laplace-Gaussian Filtering and Smoothing for Sequential Deep Learning

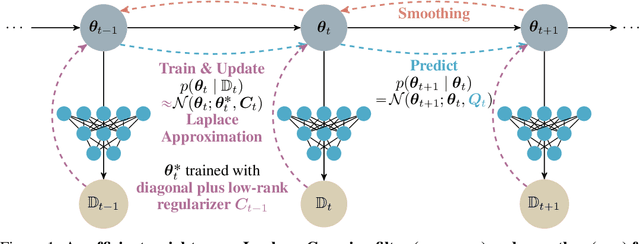
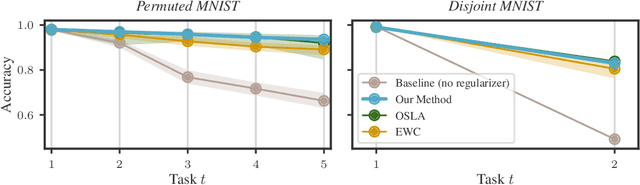
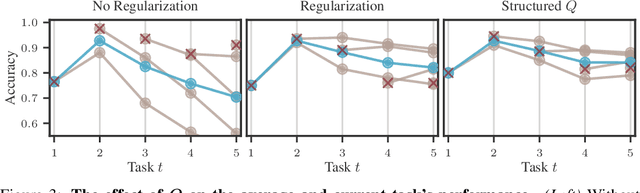
Efficiently learning a sequence of related tasks, such as in continual learning, poses a significant challenge for neural nets due to the delicate trade-off between catastrophic forgetting and loss of plasticity. We address this challenge with a grounded framework for sequentially learning related tasks based on Bayesian inference. Specifically, we treat the model's parameters as a nonlinear Gaussian state-space model and perform efficient inference using Gaussian filtering and smoothing. This general formalism subsumes existing continual learning approaches, while also offering a clearer conceptual understanding of its components. Leveraging Laplace approximations during filtering, we construct Gaussian posterior measures on the weight space of a neural network for each task. We use it as an efficient regularizer by exploiting the structure of the generalized Gauss-Newton matrix (GGN) to construct diagonal plus low-rank approximations. The dynamics model allows targeted control of the learning process and the incorporation of domain-specific knowledge, such as modeling the type of shift between tasks. Additionally, using Bayesian approximate smoothing can enhance the performance of task-specific models without needing to re-access any data.

Uncertainty-Guided Optimization on Large Language Model Search Trees

Beam search is a standard tree search algorithm when it comes to finding sequences of maximum likelihood, for example, in the decoding processes of large language models. However, it is myopic since it does not take the whole path from the root to a leaf into account. Moreover, it is agnostic to prior knowledge available about the process: For example, it does not consider that the objective being maximized is a likelihood and thereby has specific properties, like being bound in the unit interval. Taking a probabilistic approach, we define a prior belief over the LLMs' transition probabilities and obtain a posterior belief over the most promising paths in each iteration. These beliefs are helpful to define a non-myopic Bayesian-optimization-like acquisition function that allows for a more data-efficient exploration scheme than standard beam search. We discuss how to select the prior and demonstrate in on- and off-model experiments with recent large language models, including Llama-2-7b, that our method achieves higher efficiency than beam search: Our method achieves the same or a higher likelihood while expanding fewer nodes than beam search.

A Critical Look At Tokenwise Reward-Guided Text Generation

Large language models (LLMs) can significantly be improved by aligning to human preferences -- the so-called reinforcement learning from human feedback (RLHF). However, the cost of fine-tuning an LLM is prohibitive for many users. Due to their ability to bypass LLM finetuning, tokenwise reward-guided text generation (RGTG) methods have recently been proposed. They use a reward model trained on full sequences to score partial sequences during a tokenwise decoding, in a bid to steer the generation towards sequences with high rewards. However, these methods have so far been only heuristically motivated and poorly analyzed. In this work, we show that reward models trained on full sequences are not compatible with scoring partial sequences. To alleviate this issue, we propose to explicitly train a Bradley-Terry reward model on partial sequences, and autoregressively sample from the implied tokenwise policy during decoding time. We study the property of this reward model and the implied policy. In particular, we show that this policy is proportional to the ratio of two distinct RLHF policies. We show that our simple approach outperforms previous RGTG methods and achieves similar performance as strong offline baselines but without large-scale LLM finetuning.

How Useful is Intermittent, Asynchronous Expert Feedback for Bayesian Optimization?

Bayesian optimization (BO) is an integral part of automated scientific discovery -- the so-called self-driving lab -- where human inputs are ideally minimal or at least non-blocking. However, scientists often have strong intuition, and thus human feedback is still useful. Nevertheless, prior works in enhancing BO with expert feedback, such as by incorporating it in an offline or online but blocking (arrives at each BO iteration) manner, are incompatible with the spirit of self-driving labs. In this work, we study whether a small amount of randomly arriving expert feedback that is being incorporated in a non-blocking manner can improve a BO campaign. To this end, we run an additional, independent computing thread on top of the BO loop to handle the feedback-gathering process. The gathered feedback is used to learn a Bayesian preference model that can readily be incorporated into the BO thread, to steer its exploration-exploitation process. Experiments on toy and chemistry datasets suggest that even just a few intermittent, asynchronous expert feedback can be useful for improving or constraining BO. This can especially be useful for its implication in improving self-driving labs, e.g. making them more data-efficient and less costly.

A Sober Look at LLMs for Material Discovery: Are They Actually Good for Bayesian Optimization Over Molecules?

Automation is one of the cornerstones of contemporary material discovery. Bayesian optimization (BO) is an essential part of such workflows, enabling scientists to leverage prior domain knowledge into efficient exploration of a large molecular space. While such prior knowledge can take many forms, there has been significant fanfare around the ancillary scientific knowledge encapsulated in large language models (LLMs). However, existing work thus far has only explored LLMs for heuristic materials searches. Indeed, recent work obtains the uncertainty estimate -- an integral part of BO -- from point-estimated, non-Bayesian LLMs. In this work, we study the question of whether LLMs are actually useful to accelerate principled Bayesian optimization in the molecular space. We take a sober, dispassionate stance in answering this question. This is done by carefully (i) viewing LLMs as fixed feature extractors for standard but principled BO surrogate models and by (ii) leveraging parameter-efficient finetuning methods and Bayesian neural networks to obtain the posterior of the LLM surrogate. Our extensive experiments with real-world chemistry problems show that LLMs can be useful for BO over molecules, but only if they have been pretrained or finetuned with domain-specific data.