Uncertainty-Guided Optimization on Large Language Model Search Trees

Beam search is a standard tree search algorithm when it comes to finding sequences of maximum likelihood, for example, in the decoding processes of large language models. However, it is myopic since it does not take the whole path from the root to a leaf into account. Moreover, it is agnostic to prior knowledge available about the process: For example, it does not consider that the objective being maximized is a likelihood and thereby has specific properties, like being bound in the unit interval. Taking a probabilistic approach, we define a prior belief over the LLMs' transition probabilities and obtain a posterior belief over the most promising paths in each iteration. These beliefs are helpful to define a non-myopic Bayesian-optimization-like acquisition function that allows for a more data-efficient exploration scheme than standard beam search. We discuss how to select the prior and demonstrate in on- and off-model experiments with recent large language models, including Llama-2-7b, that our method achieves higher efficiency than beam search: Our method achieves the same or a higher likelihood while expanding fewer nodes than beam search.

A Critical Look At Tokenwise Reward-Guided Text Generation

Large language models (LLMs) can significantly be improved by aligning to human preferences -- the so-called reinforcement learning from human feedback (RLHF). However, the cost of fine-tuning an LLM is prohibitive for many users. Due to their ability to bypass LLM finetuning, tokenwise reward-guided text generation (RGTG) methods have recently been proposed. They use a reward model trained on full sequences to score partial sequences during a tokenwise decoding, in a bid to steer the generation towards sequences with high rewards. However, these methods have so far been only heuristically motivated and poorly analyzed. In this work, we show that reward models trained on full sequences are not compatible with scoring partial sequences. To alleviate this issue, we propose to explicitly train a Bradley-Terry reward model on partial sequences, and autoregressively sample from the implied tokenwise policy during decoding time. We study the property of this reward model and the implied policy. In particular, we show that this policy is proportional to the ratio of two distinct RLHF policies. We show that our simple approach outperforms previous RGTG methods and achieves similar performance as strong offline baselines but without large-scale LLM finetuning.

Optimistic Optimization of Gaussian Process Samples

Bayesian optimization is a popular formalism for global optimization, but its computational costs limit it to expensive-to-evaluate functions. A competing, computationally more efficient, global optimization framework is optimistic optimization, which exploits prior knowledge about the geometry of the search space in form of a dissimilarity function. We investigate to which degree the conceptual advantages of Bayesian Optimization can be combined with the computational efficiency of optimistic optimization. By mapping the kernel to a dissimilarity, we obtain an optimistic optimization algorithm for the Bayesian Optimization setting with a run-time of up to $\mathcal{O}(N \log N)$. As a high-level take-away we find that, when using stationary kernels on objectives of relatively low evaluation cost, optimistic optimization can be strongly preferable over Bayesian optimization, while for strongly coupled and parametric models, good implementations of Bayesian optimization can perform much better, even at low evaluation cost. We argue that there is a new research domain between geometric and probabilistic search, i.e. methods that run drastically faster than traditional Bayesian optimization, while retaining some of the crucial functionality of Bayesian optimization.

Probabilistic DAG Search

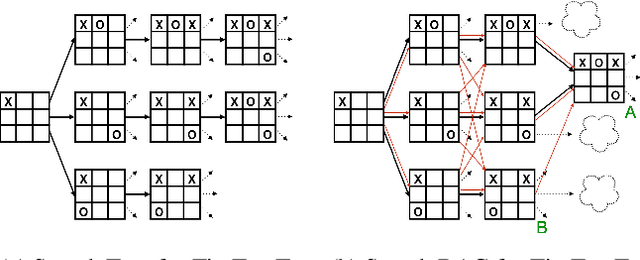
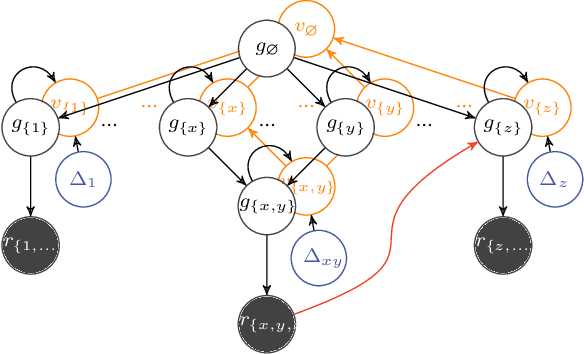
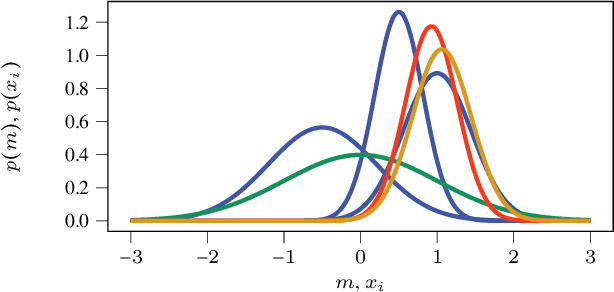
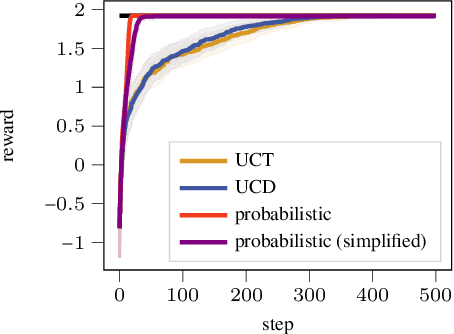
Exciting contemporary machine learning problems have recently been phrased in the classic formalism of tree search -- most famously, the game of Go. Interestingly, the state-space underlying these sequential decision-making problems often posses a more general latent structure than can be captured by a tree. In this work, we develop a probabilistic framework to exploit a search space's latent structure and thereby share information across the search tree. The method is based on a combination of approximate inference in jointly Gaussian models for the explored part of the problem, and an abstraction for the unexplored part that imposes a reduction of complexity ad hoc. We empirically find our algorithm to compare favorably to existing non-probabilistic alternatives in Tic-Tac-Toe and a feature selection application.