Probabilistic DAG Search
Paper and Code
Jun 16, 2021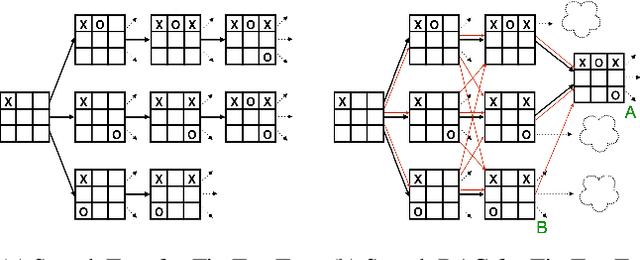
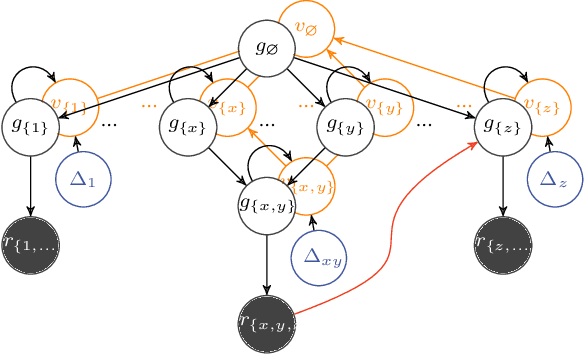
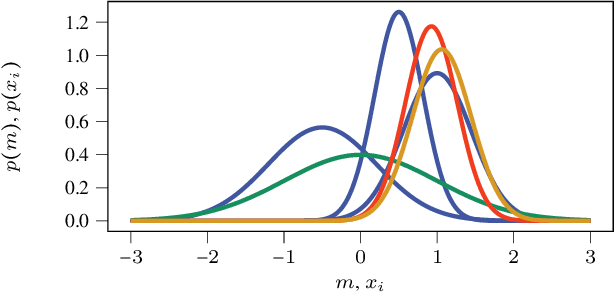
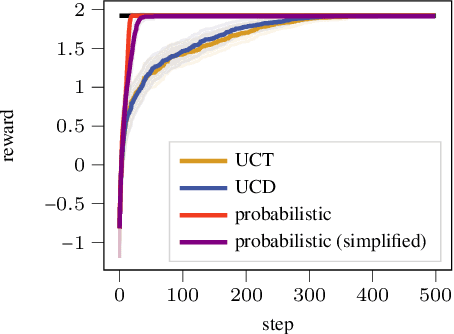
Exciting contemporary machine learning problems have recently been phrased in the classic formalism of tree search -- most famously, the game of Go. Interestingly, the state-space underlying these sequential decision-making problems often posses a more general latent structure than can be captured by a tree. In this work, we develop a probabilistic framework to exploit a search space's latent structure and thereby share information across the search tree. The method is based on a combination of approximate inference in jointly Gaussian models for the explored part of the problem, and an abstraction for the unexplored part that imposes a reduction of complexity ad hoc. We empirically find our algorithm to compare favorably to existing non-probabilistic alternatives in Tic-Tac-Toe and a feature selection application.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge