Efficient Weight-Space Laplace-Gaussian Filtering and Smoothing for Sequential Deep Learning
Paper and Code
Oct 09, 2024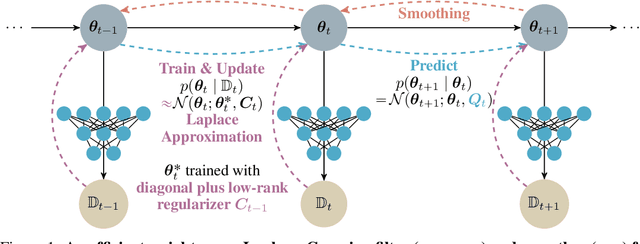
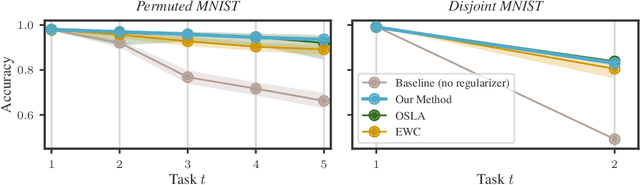

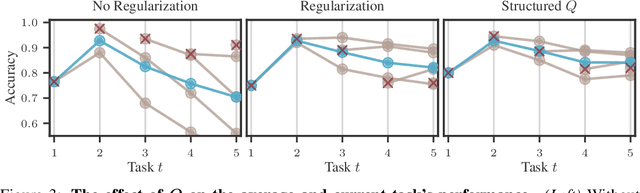
Efficiently learning a sequence of related tasks, such as in continual learning, poses a significant challenge for neural nets due to the delicate trade-off between catastrophic forgetting and loss of plasticity. We address this challenge with a grounded framework for sequentially learning related tasks based on Bayesian inference. Specifically, we treat the model's parameters as a nonlinear Gaussian state-space model and perform efficient inference using Gaussian filtering and smoothing. This general formalism subsumes existing continual learning approaches, while also offering a clearer conceptual understanding of its components. Leveraging Laplace approximations during filtering, we construct Gaussian posterior measures on the weight space of a neural network for each task. We use it as an efficient regularizer by exploiting the structure of the generalized Gauss-Newton matrix (GGN) to construct diagonal plus low-rank approximations. The dynamics model allows targeted control of the learning process and the incorporation of domain-specific knowledge, such as modeling the type of shift between tasks. Additionally, using Bayesian approximate smoothing can enhance the performance of task-specific models without needing to re-access any data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge