Nathanael Bosch
Propagating Model Uncertainty through Filtering-based Probabilistic Numerical ODE Solvers
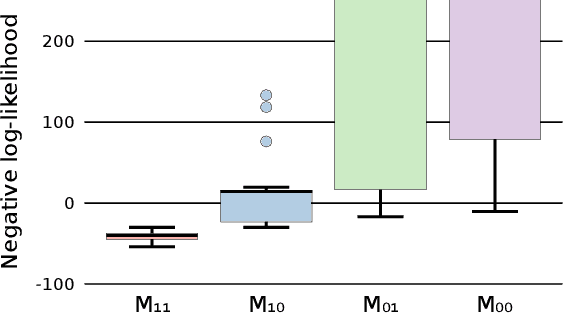
Mar 06, 2025Abstract:Filtering-based probabilistic numerical solvers for ordinary differential equations (ODEs), also known as ODE filters, have been established as efficient methods for quantifying numerical uncertainty in the solution of ODEs. In practical applications, however, the underlying dynamical system often contains uncertain parameters, requiring the propagation of this model uncertainty to the ODE solution. In this paper, we demonstrate that ODE filters, despite their probabilistic nature, do not automatically solve this uncertainty propagation problem. To address this limitation, we present a novel approach that combines ODE filters with numerical quadrature to properly marginalize over uncertain parameters, while accounting for both parameter uncertainty and numerical solver uncertainty. Experiments across multiple dynamical systems demonstrate that the resulting uncertainty estimates closely match reference solutions. Notably, we show how the numerical uncertainty from the ODE solver can help prevent overconfidence in the propagated uncertainty estimates, especially when using larger step sizes. Our results illustrate that probabilistic numerical methods can effectively quantify both numerical and parametric uncertainty in dynamical systems.
Efficient Weight-Space Laplace-Gaussian Filtering and Smoothing for Sequential Deep Learning
Oct 09, 2024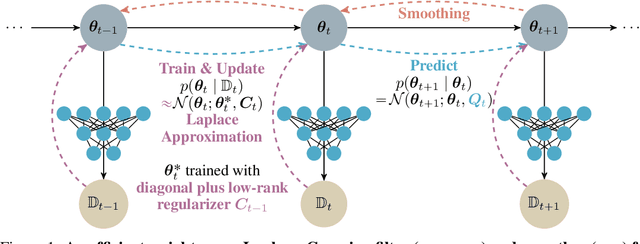
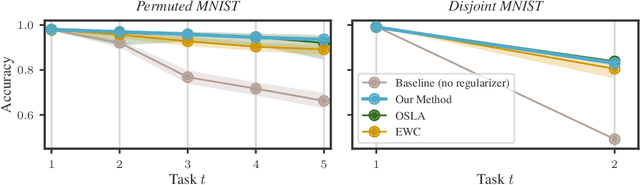

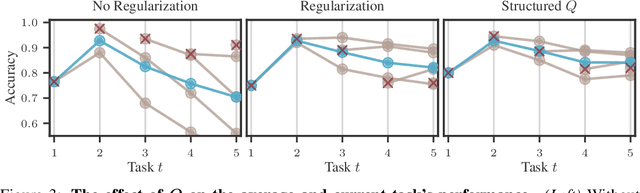
Abstract:Efficiently learning a sequence of related tasks, such as in continual learning, poses a significant challenge for neural nets due to the delicate trade-off between catastrophic forgetting and loss of plasticity. We address this challenge with a grounded framework for sequentially learning related tasks based on Bayesian inference. Specifically, we treat the model's parameters as a nonlinear Gaussian state-space model and perform efficient inference using Gaussian filtering and smoothing. This general formalism subsumes existing continual learning approaches, while also offering a clearer conceptual understanding of its components. Leveraging Laplace approximations during filtering, we construct Gaussian posterior measures on the weight space of a neural network for each task. We use it as an efficient regularizer by exploiting the structure of the generalized Gauss-Newton matrix (GGN) to construct diagonal plus low-rank approximations. The dynamics model allows targeted control of the learning process and the incorporation of domain-specific knowledge, such as modeling the type of shift between tasks. Additionally, using Bayesian approximate smoothing can enhance the performance of task-specific models without needing to re-access any data.
Diffusion Tempering Improves Parameter Estimation with Probabilistic Integrators for Ordinary Differential Equations
Feb 19, 2024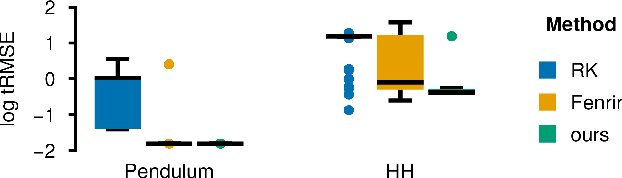
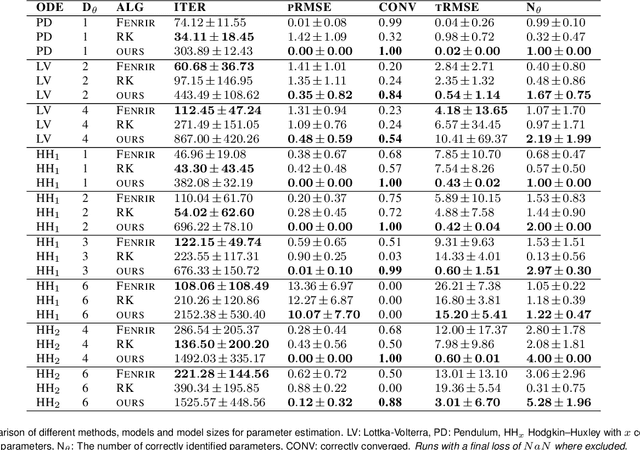
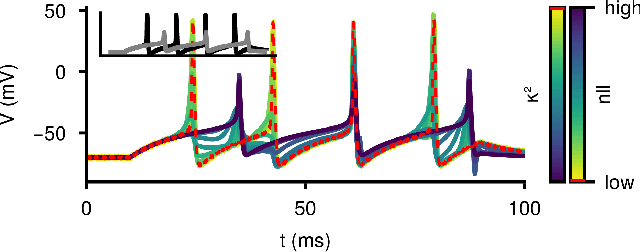

Abstract:Ordinary differential equations (ODEs) are widely used to describe dynamical systems in science, but identifying parameters that explain experimental measurements is challenging. In particular, although ODEs are differentiable and would allow for gradient-based parameter optimization, the nonlinear dynamics of ODEs often lead to many local minima and extreme sensitivity to initial conditions. We therefore propose diffusion tempering, a novel regularization technique for probabilistic numerical methods which improves convergence of gradient-based parameter optimization in ODEs. By iteratively reducing a noise parameter of the probabilistic integrator, the proposed method converges more reliably to the true parameters. We demonstrate that our method is effective for dynamical systems of different complexity and show that it obtains reliable parameter estimates for a Hodgkin-Huxley model with a practically relevant number of parameters.
Parallel-in-Time Probabilistic Numerical ODE Solvers
Oct 02, 2023Abstract:Probabilistic numerical solvers for ordinary differential equations (ODEs) treat the numerical simulation of dynamical systems as problems of Bayesian state estimation. Aside from producing posterior distributions over ODE solutions and thereby quantifying the numerical approximation error of the method itself, one less-often noted advantage of this formalism is the algorithmic flexibility gained by formulating numerical simulation in the framework of Bayesian filtering and smoothing. In this paper, we leverage this flexibility and build on the time-parallel formulation of iterated extended Kalman smoothers to formulate a parallel-in-time probabilistic numerical ODE solver. Instead of simulating the dynamical system sequentially in time, as done by current probabilistic solvers, the proposed method processes all time steps in parallel and thereby reduces the span cost from linear to logarithmic in the number of time steps. We demonstrate the effectiveness of our approach on a variety of ODEs and compare it to a range of both classic and probabilistic numerical ODE solvers.
Probabilistic Exponential Integrators
May 24, 2023Abstract:Probabilistic solvers provide a flexible and efficient framework for simulation, uncertainty quantification, and inference in dynamical systems. However, like standard solvers, they suffer performance penalties for certain stiff systems, where small steps are required not for reasons of numerical accuracy but for the sake of stability. This issue is greatly alleviated in semi-linear problems by the probabilistic exponential integrators developed in this paper. By including the fast, linear dynamics in the prior, we arrive at a class of probabilistic integrators with favorable properties. Namely, they are proven to be L-stable, and in a certain case reduce to a classic exponential integrator -- with the added benefit of providing a probabilistic account of the numerical error. The method is also generalized to arbitrary non-linear systems by imposing piece-wise semi-linearity on the prior via Jacobians of the vector field at the previous estimates, resulting in probabilistic exponential Rosenbrock methods. We evaluate the proposed methods on multiple stiff differential equations and demonstrate their improved stability and efficiency over established probabilistic solvers. The present contribution thus expands the range of problems that can be effectively tackled within probabilistic numerics.
Fenrir: Physics-Enhanced Regression for Initial Value Problems
Feb 02, 2022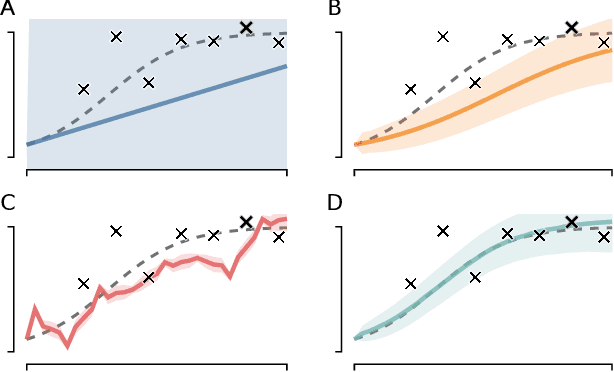
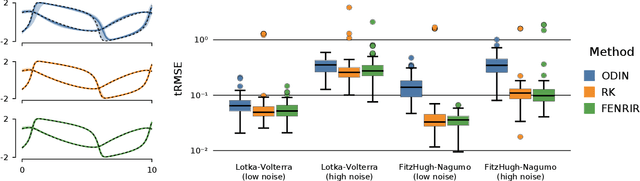
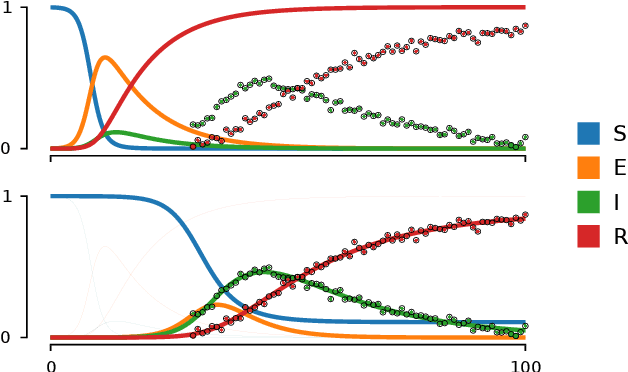
Abstract:We show how probabilistic numerics can be used to convert an initial value problem into a Gauss--Markov process parametrised by the dynamics of the initial value problem. Consequently, the often difficult problem of parameter estimation in ordinary differential equations is reduced to hyperparameter estimation in Gauss--Markov regression, which tends to be considerably easier. The method's relation and benefits in comparison to classical numerical integration and gradient matching approaches is elucidated. In particular, the method can, in contrast to gradient matching, handle partial observations, and has certain routes for escaping local optima not available to classical numerical integration. Experimental results demonstrate that the method is on par or moderately better than competing approaches.
ProbNum: Probabilistic Numerics in Python
Dec 03, 2021


Abstract:Probabilistic numerical methods (PNMs) solve numerical problems via probabilistic inference. They have been developed for linear algebra, optimization, integration and differential equation simulation. PNMs naturally incorporate prior information about a problem and quantify uncertainty due to finite computational resources as well as stochastic input. In this paper, we present ProbNum: a Python library providing state-of-the-art probabilistic numerical solvers. ProbNum enables custom composition of PNMs for specific problem classes via a modular design as well as wrappers for off-the-shelf use. Tutorials, documentation, developer guides and benchmarks are available online at www.probnum.org.
Probabilistic ODE Solutions in Millions of Dimensions
Oct 22, 2021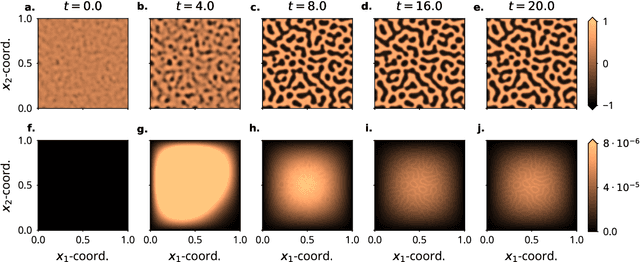
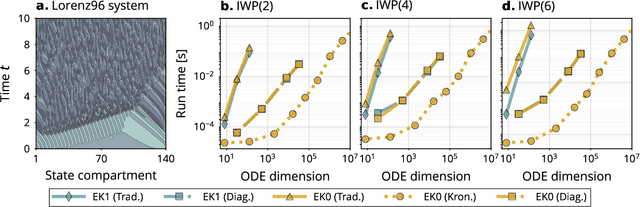
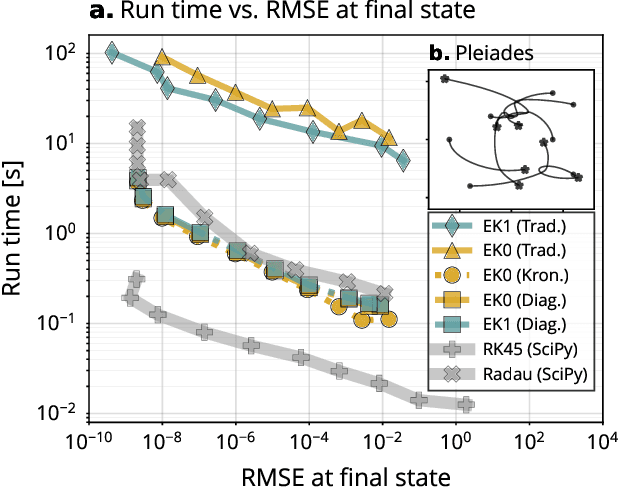
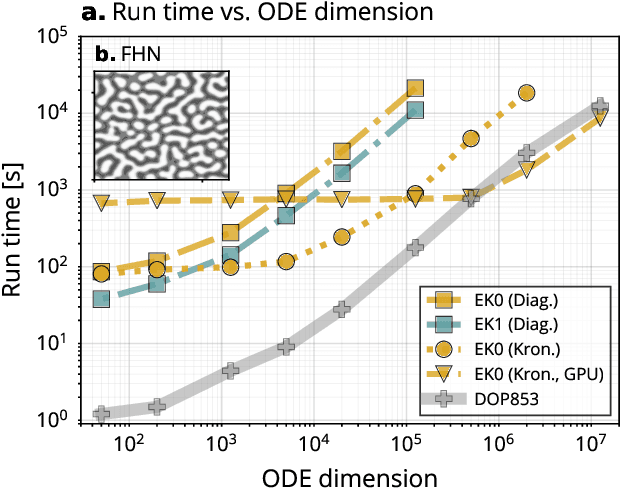
Abstract:Probabilistic solvers for ordinary differential equations (ODEs) have emerged as an efficient framework for uncertainty quantification and inference on dynamical systems. In this work, we explain the mathematical assumptions and detailed implementation schemes behind solving {high-dimensional} ODEs with a probabilistic numerical algorithm. This has not been possible before due to matrix-matrix operations in each solver step, but is crucial for scientifically relevant problems -- most importantly, the solution of discretised {partial} differential equations. In a nutshell, efficient high-dimensional probabilistic ODE solutions build either on independence assumptions or on Kronecker structure in the prior model. We evaluate the resulting efficiency on a range of problems, including the probabilistic numerical simulation of a differential equation with millions of dimensions.
Pick-and-Mix Information Operators for Probabilistic ODE Solvers
Oct 20, 2021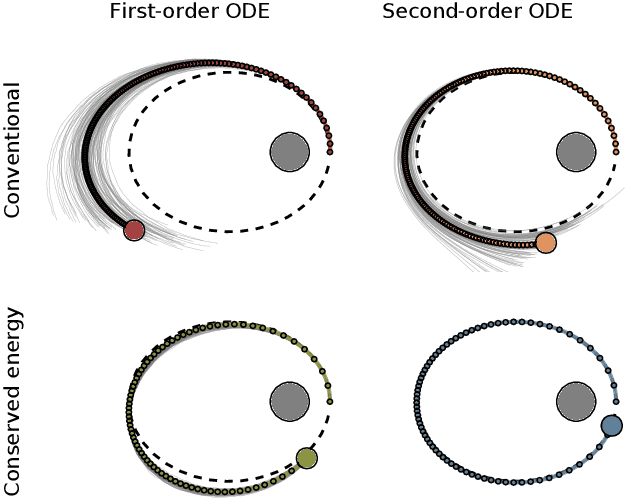

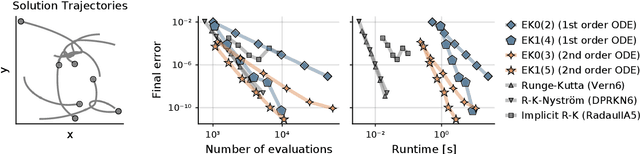
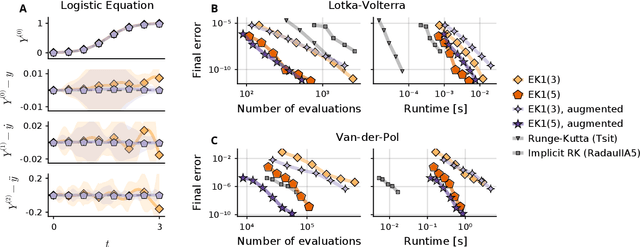
Abstract:Probabilistic numerical solvers for ordinary differential equations compute posterior distributions over the solution of an initial value problem via Bayesian inference. In this paper, we leverage their probabilistic formulation to seamlessly include additional information as general likelihood terms. We show that second-order differential equations should be directly provided to the solver, instead of transforming the problem to first order. Additionally, by including higher-order information or physical conservation laws in the model, solutions become more accurate and more physically meaningful. Lastly, we demonstrate the utility of flexible information operators by solving differential-algebraic equations. In conclusion, the probabilistic formulation of numerical solvers offers a flexible way to incorporate various types of information, thus improving the resulting solutions.
Calibrated Adaptive Probabilistic ODE Solvers
Dec 15, 2020



Abstract:Probabilistic solvers for ordinary differential equations (ODEs) assign a posterior measure to the solution of an initial value problem. The joint covariance of this distribution provides an estimate of the (global) approximation error. The contraction rate of this error estimate as a function of the solver's step size identifies it as a well-calibrated worst-case error. But its explicit numerical value for a certain step size, which depends on certain parameters of this class of solvers, is not automatically a good estimate of the explicit error. Addressing this issue, we introduce, discuss, and assess several probabilistically motivated ways to calibrate the uncertainty estimate. Numerical experiments demonstrate that these calibration methods interact efficiently with adaptive step-size selection, resulting in descriptive, and efficiently computable posteriors. We demonstrate the efficiency of the methodology by benchmarking against the classic, widely used Dormand-Prince 4/5 Runge-Kutta method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge