Jonathan Schmidt
Department of Materials, ETH Zürich, Zürich, Switzerland
AI-Driven Expansion and Application of the Alexandria Database
Dec 09, 2025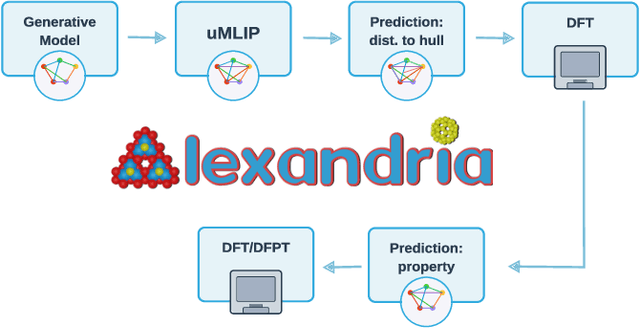
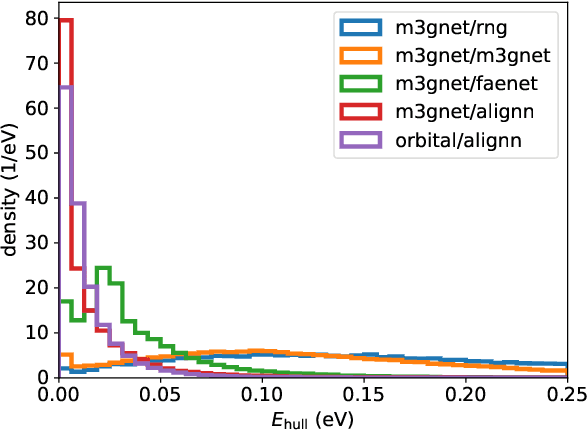
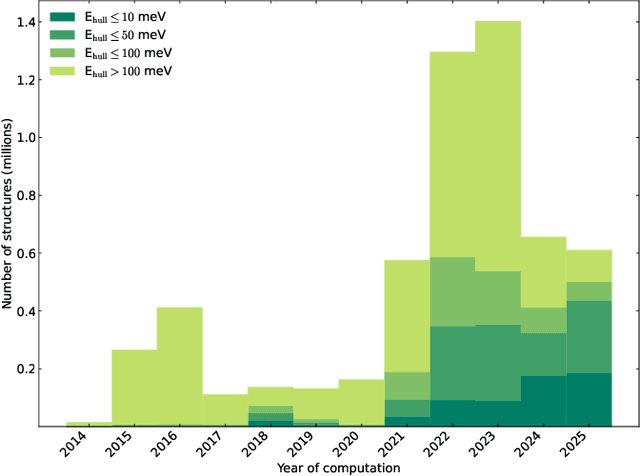
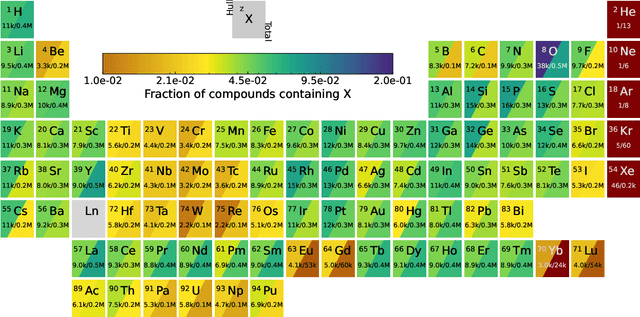
Abstract:We present a novel multi-stage workflow for computational materials discovery that achieves a 99% success rate in identifying compounds within 100 meV/atom of thermodynamic stability, with a threefold improvement over previous approaches. By combining the Matra-Genoa generative model, Orb-v2 universal machine learning interatomic potential, and ALIGNN graph neural network for energy prediction, we generated 119 million candidate structures and added 1.3 million DFT-validated compounds to the ALEXANDRIA database, including 74 thousand new stable materials. The expanded ALEXANDRIA database now contains 5.8 million structures with 175 thousand compounds on the convex hull. Predicted structural disorder rates (37-43%) match experimental databases, unlike other recent AI-generated datasets. Analysis reveals fundamental patterns in space group distributions, coordination environments, and phase stability networks, including sub-linear scaling of convex hull connectivity. We release the complete dataset, including sAlex25 with 14 million out-of-equilibrium structures containing forces and stresses for training universal force fields. We demonstrate that fine-tuning a GRACE model on this data improves benchmark accuracy. All data, models, and workflows are freely available under Creative Commons licenses.
BecomingLit: Relightable Gaussian Avatars with Hybrid Neural Shading
Jun 06, 2025Abstract:We introduce BecomingLit, a novel method for reconstructing relightable, high-resolution head avatars that can be rendered from novel viewpoints at interactive rates. Therefore, we propose a new low-cost light stage capture setup, tailored specifically towards capturing faces. Using this setup, we collect a novel dataset consisting of diverse multi-view sequences of numerous subjects under varying illumination conditions and facial expressions. By leveraging our new dataset, we introduce a new relightable avatar representation based on 3D Gaussian primitives that we animate with a parametric head model and an expression-dependent dynamics module. We propose a new hybrid neural shading approach, combining a neural diffuse BRDF with an analytical specular term. Our method reconstructs disentangled materials from our dynamic light stage recordings and enables all-frequency relighting of our avatars with both point lights and environment maps. In addition, our avatars can easily be animated and controlled from monocular videos. We validate our approach in extensive experiments on our dataset, where we consistently outperform existing state-of-the-art methods in relighting and reenactment by a significant margin.
Spatiotemporally Coherent Probabilistic Generation of Weather from Climate
Dec 19, 2024Abstract:Local climate information is crucial for impact assessment and decision-making, yet coarse global climate simulations cannot capture small-scale phenomena. Current statistical downscaling methods infer these phenomena as temporally decoupled spatial patches. However, to preserve physical properties, estimating spatio-temporally coherent high-resolution weather dynamics for multiple variables across long time horizons is crucial. We present a novel generative approach that uses a score-based diffusion model trained on high-resolution reanalysis data to capture the statistical properties of local weather dynamics. After training, we condition on coarse climate model data to generate weather patterns consistent with the aggregate information. As this inference task is inherently uncertain, we leverage the probabilistic nature of diffusion models and sample multiple trajectories. We evaluate our approach with high-resolution reanalysis information before applying it to the climate model downscaling task. We then demonstrate that the model generates spatially and temporally coherent weather dynamics that align with global climate output.
LiDAR View Synthesis for Robust Vehicle Navigation Without Expert Labels
Aug 05, 2023Abstract:Deep learning models for self-driving cars require a diverse training dataset to manage critical driving scenarios on public roads safely. This includes having data from divergent trajectories, such as the oncoming traffic lane or sidewalks. Such data would be too dangerous to collect in the real world. Data augmentation approaches have been proposed to tackle this issue using RGB images. However, solutions based on LiDAR sensors are scarce. Therefore, we propose synthesizing additional LiDAR point clouds from novel viewpoints without physically driving at dangerous positions. The LiDAR view synthesis is done using mesh reconstruction and ray casting. We train a deep learning model, which takes a LiDAR scan as input and predicts the future trajectory as output. A waypoint controller is then applied to this predicted trajectory to determine the throttle and steering labels of the ego-vehicle. Our method neither requires expert driving labels for the original nor the synthesized LiDAR sequence. Instead, we infer labels from LiDAR odometry. We demonstrate the effectiveness of our approach in a comprehensive online evaluation and with a comparison to concurrent work. Our results show the importance of synthesizing additional LiDAR point clouds, particularly in terms of model robustness. Project page: https://jonathsch.github.io/lidar-synthesis/
The Rank-Reduced Kalman Filter: Approximate Dynamical-Low-Rank Filtering In High Dimensions
Jun 28, 2023Abstract:Inference and simulation in the context of high-dimensional dynamical systems remain computationally challenging problems. Some form of dimensionality reduction is required to make the problem tractable in general. In this paper, we propose a novel approximate Gaussian filtering and smoothing method which propagates low-rank approximations of the covariance matrices. This is accomplished by projecting the Lyapunov equations associated with the prediction step to a manifold of low-rank matrices, which are then solved by a recently developed, numerically stable, dynamical low-rank integrator. Meanwhile, the update steps are made tractable by noting that the covariance update only transforms the column space of the covariance matrix, which is low-rank by construction. The algorithm differentiates itself from existing ensemble-based approaches in that the low-rank approximations of the covariance matrices are deterministic, rather than stochastic. Crucially, this enables the method to reproduce the exact Kalman filter as the low-rank dimension approaches the true dimensionality of the problem. Our method reduces computational complexity from cubic (for the Kalman filter) to \emph{quadratic} in the state-space size in the worst-case, and can achieve \emph{linear} complexity if the state-space model satisfies certain criteria. Through a set of experiments in classical data-assimilation and spatio-temporal regression, we show that the proposed method consistently outperforms the ensemble-based methods in terms of error in the mean and covariance with respect to the exact Kalman filter. This comes at no additional cost in terms of asymptotic computational complexity.
Large-scale machine-learning-assisted exploration of the whole materials space
Oct 02, 2022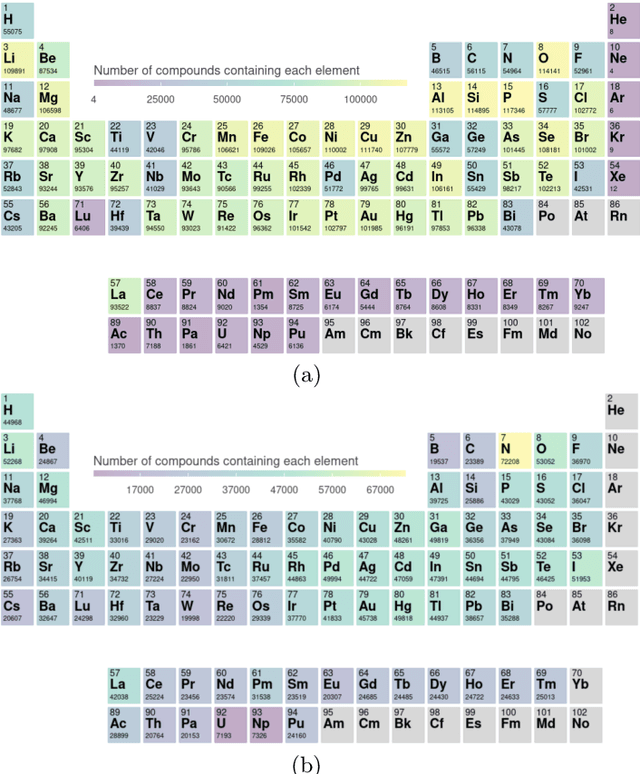
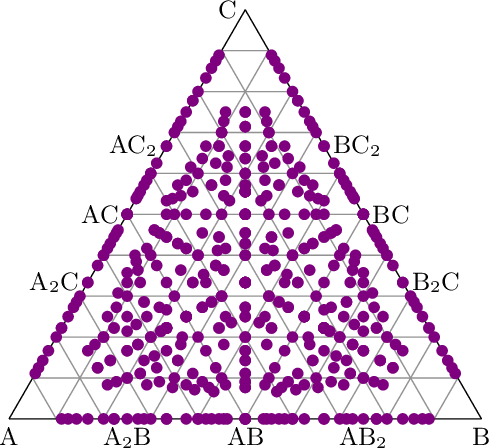
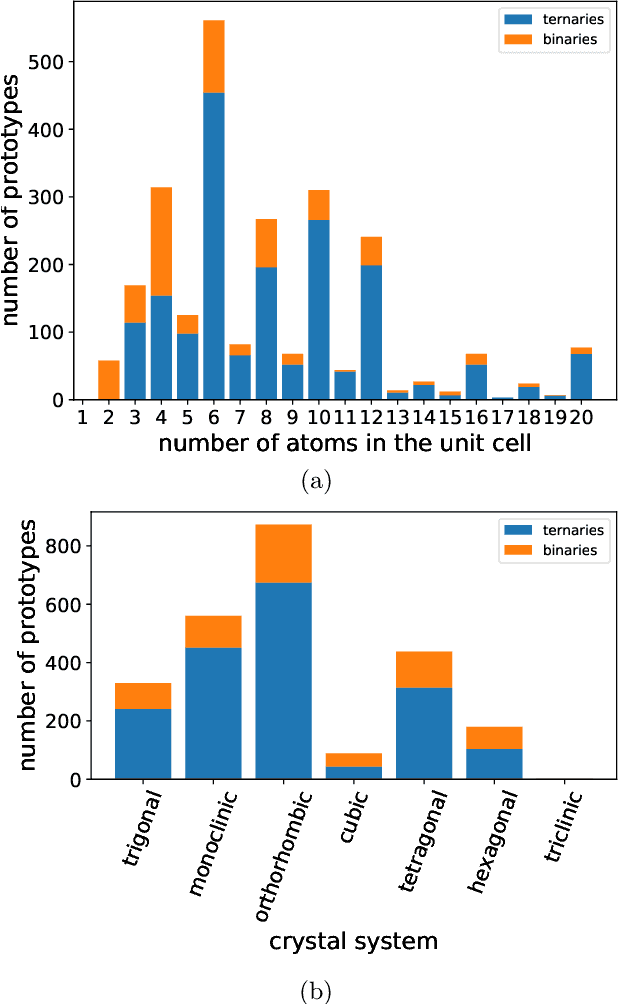
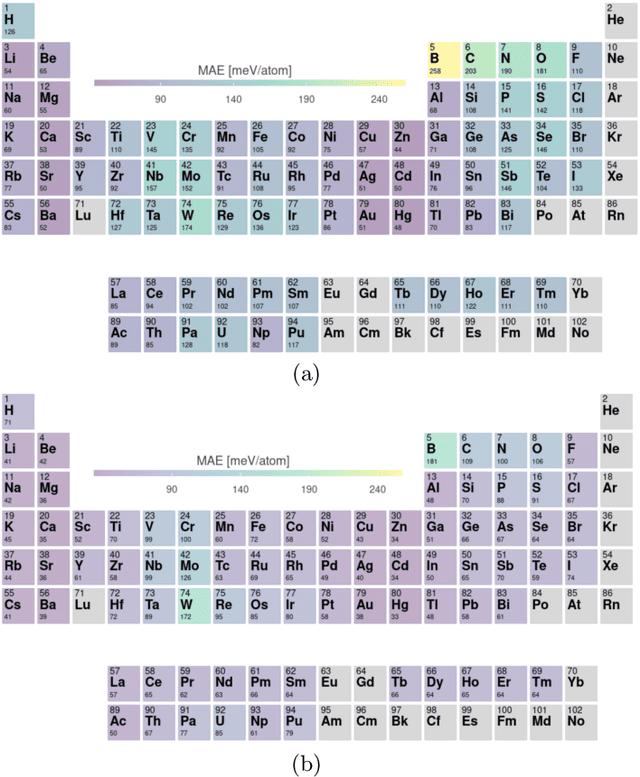
Abstract:Crystal-graph attention networks have emerged recently as remarkable tools for the prediction of thermodynamic stability and materials properties from unrelaxed crystal structures. Previous networks trained on two million materials exhibited, however, strong biases originating from underrepresented chemical elements and structural prototypes in the available data. We tackled this issue computing additional data to provide better balance across both chemical and crystal-symmetry space. Crystal-graph networks trained with this new data show unprecedented generalization accuracy, and allow for reliable, accelerated exploration of the whole space of inorganic compounds. We applied this universal network to perform machine-learning assisted high-throughput materials searches including 2500 binary and ternary structure prototypes and spanning about 1 billion compounds. After validation using density-functional theory, we uncover in total 19512 additional materials on the convex hull of thermodynamic stability and ~150000 compounds with a distance of less than 50 meV/atom from the hull. Combining again machine learning and ab-initio methods, we finally evaluate the discovered materials for applications as superconductors, superhard materials, and we look for candidates with large gap deformation potentials, finding several compounds with extreme values of these properties.
Machine Learning guided high-throughput search of non-oxide garnets
Aug 29, 2022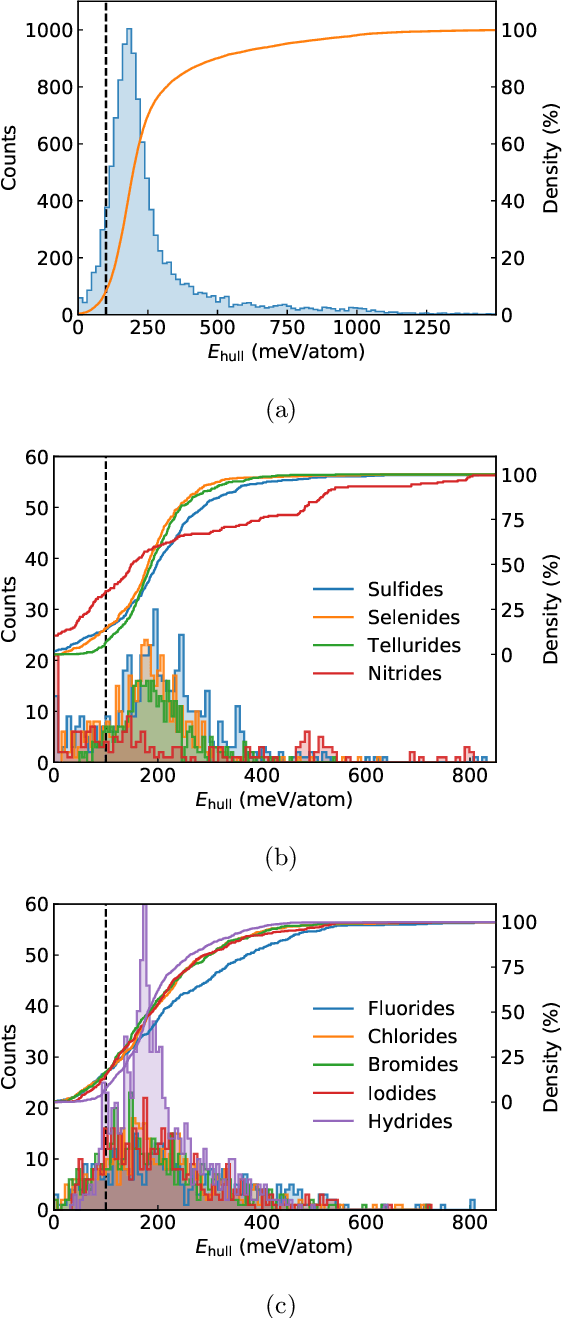
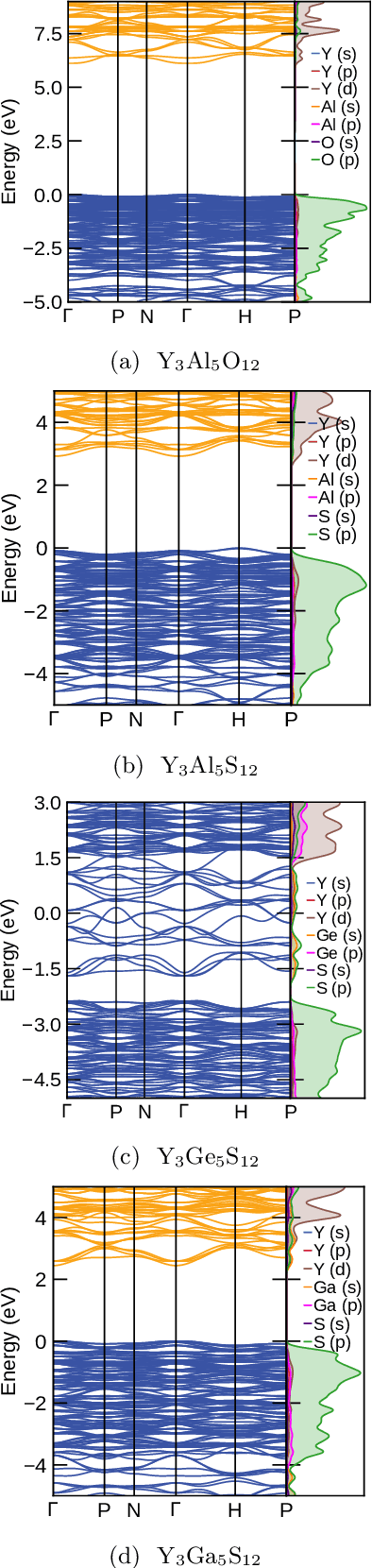
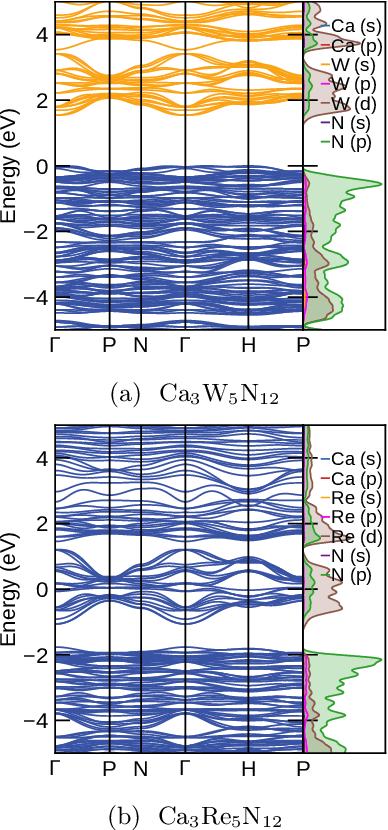
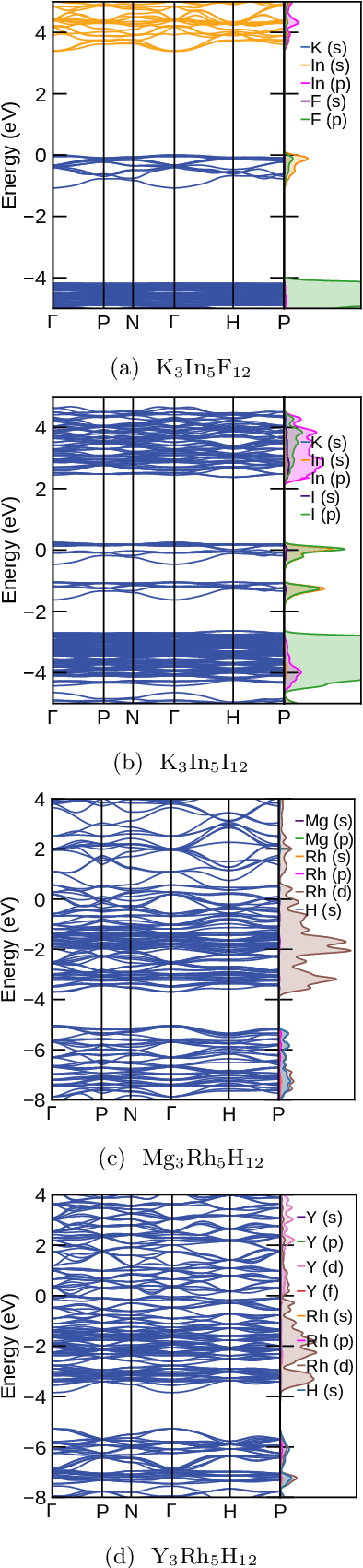
Abstract:Garnets, known since the early stages of human civilization, have found important applications in modern technologies including magnetorestriction, spintronics, lithium batteries, etc. The overwhelming majority of experimentally known garnets are oxides, while explorations (experimental or theoretical) for the rest of the chemical space have been limited in scope. A key issue is that the garnet structure has a large primitive unit cell, requiring an enormous amount of computational resources. To perform a comprehensive search of the complete chemical space for new garnets,we combine recent progress in graph neural networks with high-throughput calculations. We apply the machine learning model to identify the potential (meta-)stable garnet systems before systematic density-functional calculations to validate the predictions. In this way, we discover more than 600 ternary garnets with distances to the convex hull below 100~meV/atom with a variety of physical and chemical properties. This includes sulfide, nitride and halide garnets. For these, we analyze the electronic structure and discuss the connection between the value of the electronic band gap and charge balance.
ProbNum: Probabilistic Numerics in Python
Dec 03, 2021


Abstract:Probabilistic numerical methods (PNMs) solve numerical problems via probabilistic inference. They have been developed for linear algebra, optimization, integration and differential equation simulation. PNMs naturally incorporate prior information about a problem and quantify uncertainty due to finite computational resources as well as stochastic input. In this paper, we present ProbNum: a Python library providing state-of-the-art probabilistic numerical solvers. ProbNum enables custom composition of PNMs for specific problem classes via a modular design as well as wrappers for off-the-shelf use. Tutorials, documentation, developer guides and benchmarks are available online at www.probnum.org.
Probabilistic Numerical Method of Lines for Time-Dependent Partial Differential Equations
Oct 22, 2021
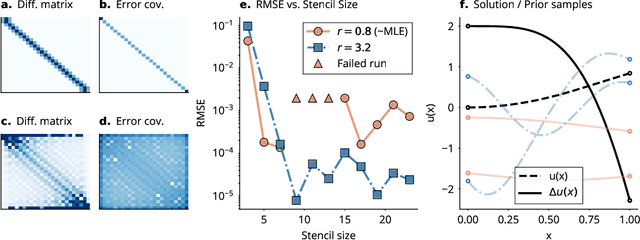
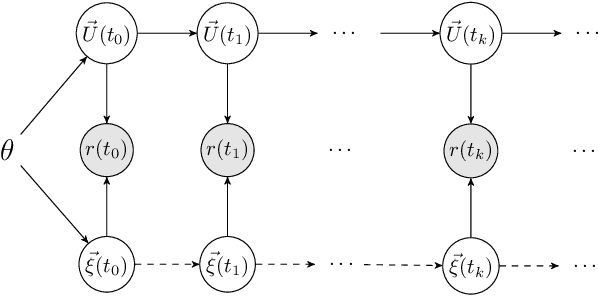
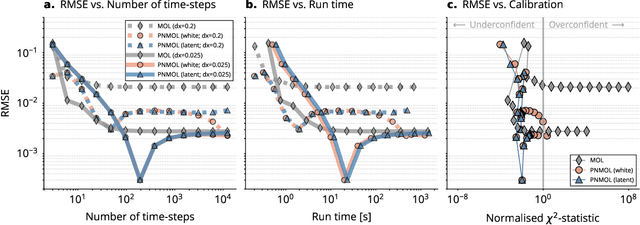
Abstract:This work develops a class of probabilistic algorithms for the numerical solution of nonlinear, time-dependent partial differential equations (PDEs). Current state-of-the-art PDE solvers treat the space- and time-dimensions separately, serially, and with black-box algorithms, which obscures the interactions between spatial and temporal approximation errors and misguides the quantification of the overall error. To fix this issue, we introduce a probabilistic version of a technique called method of lines. The proposed algorithm begins with a Gaussian process interpretation of finite difference methods, which then interacts naturally with filtering-based probabilistic ordinary differential equation (ODE) solvers because they share a common language: Bayesian inference. Joint quantification of space- and time-uncertainty becomes possible without losing the performance benefits of well-tuned ODE solvers. Thereby, we extend the toolbox of probabilistic programs for differential equation simulation to PDEs.
Probabilistic ODE Solutions in Millions of Dimensions
Oct 22, 2021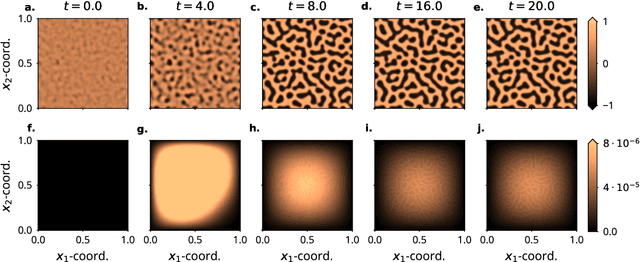
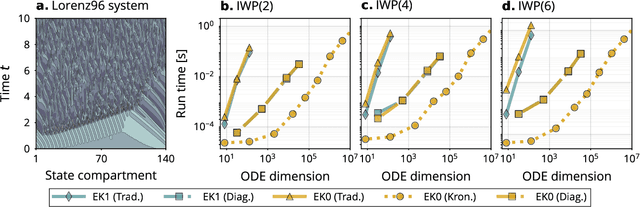
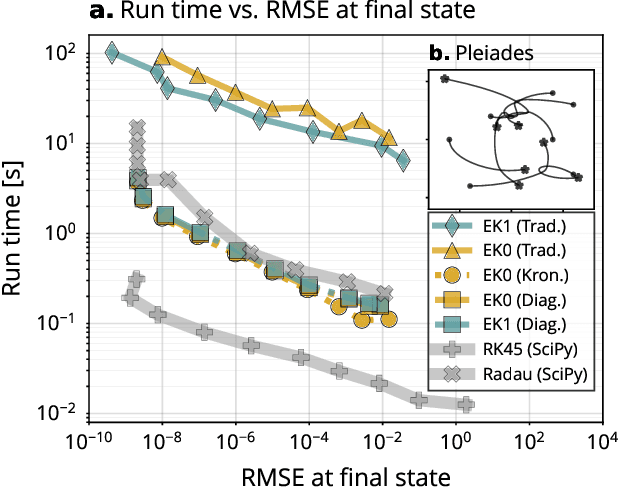
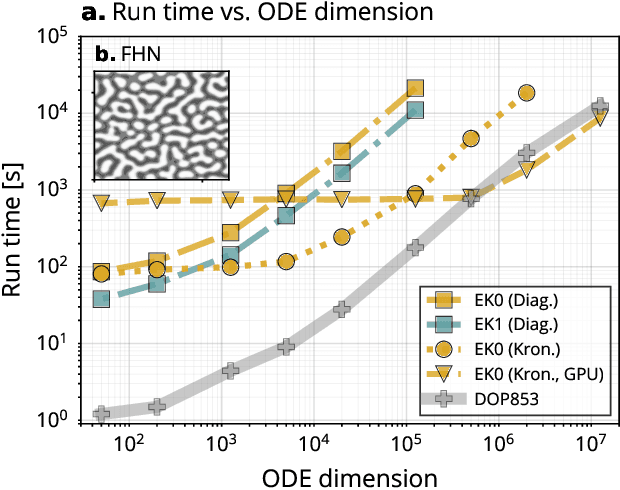
Abstract:Probabilistic solvers for ordinary differential equations (ODEs) have emerged as an efficient framework for uncertainty quantification and inference on dynamical systems. In this work, we explain the mathematical assumptions and detailed implementation schemes behind solving {high-dimensional} ODEs with a probabilistic numerical algorithm. This has not been possible before due to matrix-matrix operations in each solver step, but is crucial for scientifically relevant problems -- most importantly, the solution of discretised {partial} differential equations. In a nutshell, efficient high-dimensional probabilistic ODE solutions build either on independence assumptions or on Kronecker structure in the prior model. We evaluate the resulting efficiency on a range of problems, including the probabilistic numerical simulation of a differential equation with millions of dimensions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge