Stationary MMD Points for Cubature

Approximation of a target probability distribution using a finite set of points is a problem of fundamental importance, arising in cubature, data compression, and optimisation. Several authors have proposed to select points by minimising a maximum mean discrepancy (MMD), but the non-convexity of this objective precludes global minimisation in general. Instead, we consider \emph{stationary} points of the MMD which, in contrast to points globally minimising the MMD, can be accurately computed. Our main theoretical contribution is the (perhaps surprising) result that, for integrands in the associated reproducing kernel Hilbert space, the cubature error of stationary MMD points vanishes \emph{faster} than the MMD. Motivated by this \emph{super-convergence} property, we consider discretised gradient flows as a practical strategy for computing stationary points of the MMD, presenting a refined convergence analysis that establishes a novel non-asymptotic finite-particle error bound, which may be of independent interest.

A Dictionary of Closed-Form Kernel Mean Embeddings

Kernel mean embeddings -- integrals of a kernel with respect to a probability distribution -- are essential in Bayesian quadrature, but also widely used in other computational tools for numerical integration or for statistical inference based on the maximum mean discrepancy. These methods often require, or are enhanced by, the availability of a closed-form expression for the kernel mean embedding. However, deriving such expressions can be challenging, limiting the applicability of kernel-based techniques when practitioners do not have access to a closed-form embedding. This paper addresses this limitation by providing a comprehensive dictionary of known kernel mean embeddings, along with practical tools for deriving new embeddings from known ones. We also provide a Python library that includes minimal implementations of the embeddings.

Maximum mean discrepancies of Farey sequences

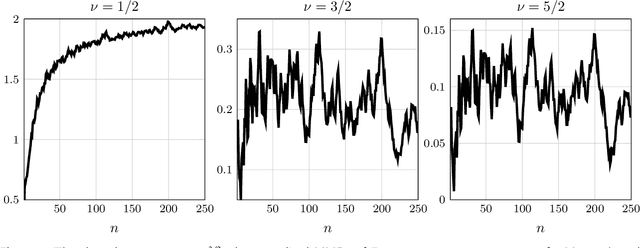
We identify a large class of positive-semidefinite kernels for which a certain polynomial rate of convergence of maximum mean discrepancies of Farey sequences is equivalent to the Riemann hypothesis. This class includes all Mat\'ern kernels of order at least one-half.

Orthonormal Expansions for Translation-Invariant Kernels

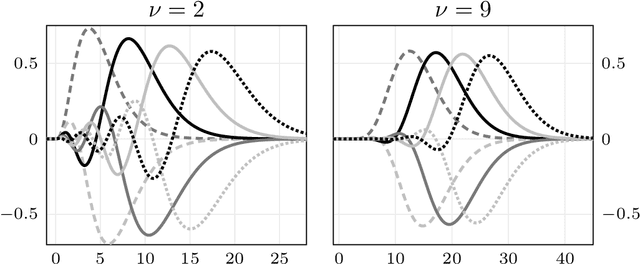
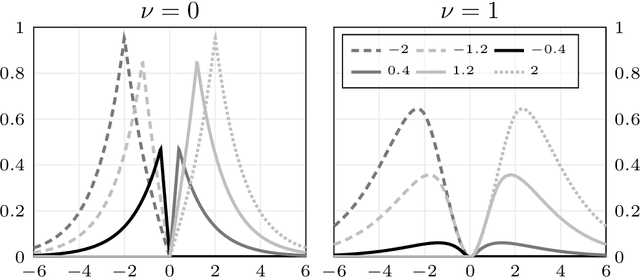
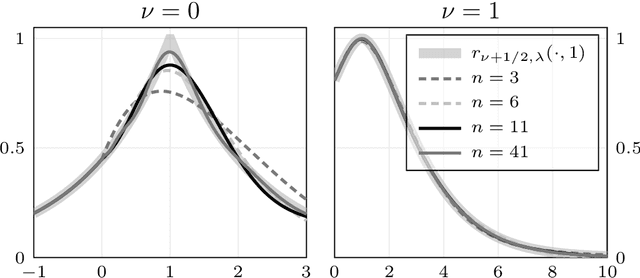
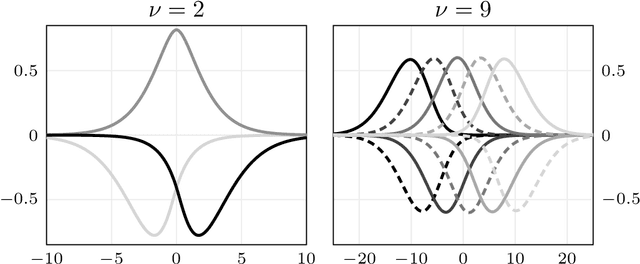
We present a general Fourier analytic technique for constructing orthonormal basis expansions of translation-invariant kernels from orthonormal bases of $\mathscr{L}_2(\mathbb{R})$. This allows us to derive explicit expansions on the real line for (i) Mat\'ern kernels of all half-integer orders in terms of associated Laguerre functions, (ii) the Cauchy kernel in terms of rational functions, and (iii) the Gaussian kernel in terms of Hermite functions.

Maximum Likelihood Estimation in Gaussian Process Regression is Ill-Posed

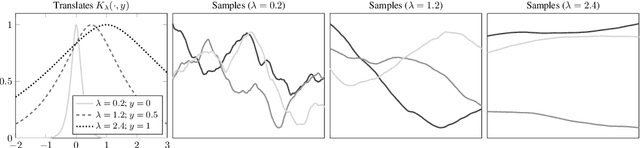
Gaussian process regression underpins countless academic and industrial applications of machine learning and statistics, with maximum likelihood estimation routinely used to select appropriate parameters for the covariance kernel. However, it remains an open problem to establish the circumstances in which maximum likelihood estimation is well-posed. That is, when the predictions of the regression model are continuous (or insensitive to small perturbations) in the training data. This article presents a rigorous proof that the maximum likelihood estimator fails to be well-posed in Hellinger distance in a scenario where the data are noiseless. The failure case occurs for any Gaussian process with a stationary covariance function whose lengthscale parameter is estimated using maximum likelihood. Although the failure of maximum likelihood estimation is informally well-known, these theoretical results appear to be the first of their kind, and suggest that well-posedness may need to be assessed post-hoc, on a case-by-case basis, when maximum likelihood estimation is used to train a Gaussian process model.

Asymptotic Bounds for Smoothness Parameter Estimates in Gaussian Process Regression

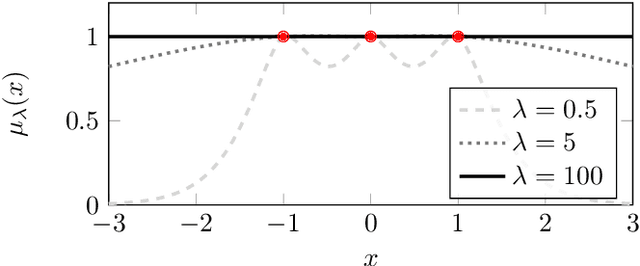
It is common to model a deterministic response function, such as the output of a computer experiment, as a Gaussian process with a Mat\'ern covariance kernel. The smoothness parameter of a Mat\'ern kernel determines many important properties of the model in the large data limit, such as the rate of convergence of the conditional mean to the response function. We prove that the maximum likelihood and cross-validation estimates of the smoothness parameter cannot asymptotically undersmooth the truth when the data are obtained on a fixed bounded subset of $\mathbb{R}^d$. That is, if the data-generating response function has Sobolev smoothness $\nu_0 + d/2$, then the smoothness parameter estimates cannot remain below $\nu_0$ as more data are obtained. These results are based on a general theorem, proved using reproducing kernel Hilbert space techniques, about sets of values the parameter estimates cannot take and approximation theory in Sobolev spaces.

ProbNum: Probabilistic Numerics in Python

Probabilistic numerical methods (PNMs) solve numerical problems via probabilistic inference. They have been developed for linear algebra, optimization, integration and differential equation simulation. PNMs naturally incorporate prior information about a problem and quantify uncertainty due to finite computational resources as well as stochastic input. In this paper, we present ProbNum: a Python library providing state-of-the-art probabilistic numerical solvers. ProbNum enables custom composition of PNMs for specific problem classes via a modular design as well as wrappers for off-the-shelf use. Tutorials, documentation, developer guides and benchmarks are available online at www.probnum.org.

Black Box Probabilistic Numerics

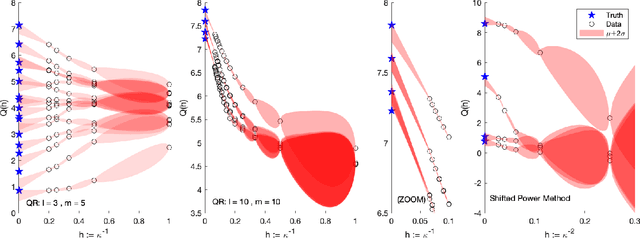
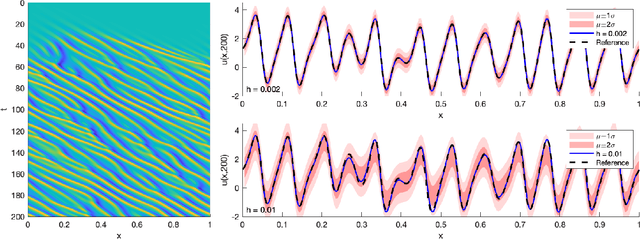
Probabilistic numerics casts numerical tasks, such the numerical solution of differential equations, as inference problems to be solved. One approach is to model the unknown quantity of interest as a random variable, and to constrain this variable using data generated during the course of a traditional numerical method. However, data may be nonlinearly related to the quantity of interest, rendering the proper conditioning of random variables difficult and limiting the range of numerical tasks that can be addressed. Instead, this paper proposes to construct probabilistic numerical methods based only on the final output from a traditional method. A convergent sequence of approximations to the quantity of interest constitute a dataset, from which the limiting quantity of interest can be extrapolated, in a probabilistic analogue of Richardson's deferred approach to the limit. This black box approach (1) massively expands the range of tasks to which probabilistic numerics can be applied, (2) inherits the features and performance of state-of-the-art numerical methods, and (3) enables provably higher orders of convergence to be achieved. Applications are presented for nonlinear ordinary and partial differential equations, as well as for eigenvalue problems-a setting for which no probabilistic numerical methods have yet been developed.

Small Sample Spaces for Gaussian Processes

It is known that the membership in a given reproducing kernel Hilbert space (RKHS) of the samples of a Gaussian process $X$ is controlled by a certain nuclear dominance condition. However, it is less clear how to identify a "small" set of functions (not necessarily a vector space) that contains the samples. This article presents a general approach for identifying such sets. We use scaled RKHSs, which can be viewed as a generalisation of Hilbert scales, to define the sample support set as the largest set which is contained in every element of full measure under the law of $X$ in the $\sigma$-algebra induced by the collection of scaled RKHS. This potentially non-measurable set is then shown to consist of those functions that can be expanded in terms of an orthonormal basis of the RKHS of the covariance kernel of $X$ and have their squared basis coefficients bounded away from zero and infinity, a result suggested by the Karhunen-Lo\`{e}ve theorem.

A Probabilistic Taylor Expansion with Applications in Filtering and Differential Equations

We study a class of Gaussian processes for which the posterior mean, for a particular choice of data, replicates a truncated Taylor expansion of any order. The data consists of derivative evaluations at the expansion point and the prior covariance kernel belongs to the class of Taylor kernels, which can be written in a certain power series form. This permits statistical modelling of the uncertainty in a variety of algorithms that exploit first and second order Taylor expansions. To demonstrate the utility of this Gaussian process model we introduce new probabilistic versions of the classical extended Kalman filter for non-linear state estimation and the Euler method for solving ordinary differential equations.