Reinforcement Learning for Adaptive MCMC

An informal observation, made by several authors, is that the adaptive design of a Markov transition kernel has the flavour of a reinforcement learning task. Yet, to-date it has remained unclear how to actually exploit modern reinforcement learning technologies for adaptive MCMC. The aim of this paper is to set out a general framework, called Reinforcement Learning Metropolis--Hastings, that is theoretically supported and empirically validated. Our principal focus is on learning fast-mixing Metropolis--Hastings transition kernels, which we cast as deterministic policies and optimise via a policy gradient. Control of the learning rate provably ensures conditions for ergodicity are satisfied. The methodology is used to construct a gradient-free sampler that out-performs a popular gradient-free adaptive Metropolis--Hastings algorithm on $\approx 90 \%$ of tasks in the PosteriorDB benchmark.

Controlling Moments with Kernel Stein Discrepancies

Quantifying the deviation of a probability distribution is challenging when the target distribution is defined by a density with an intractable normalizing constant. The kernel Stein discrepancy (KSD) was proposed to address this problem and has been applied to various tasks including diagnosing approximate MCMC samplers and goodness-of-fit testing for unnormalized statistical models. This article investigates a convergence control property of the diffusion kernel Stein discrepancy (DKSD), an instance of the KSD proposed by Barp et al. (2019). We extend the result of Gorham and Mackey (2017), which showed that the KSD controls the bounded-Lipschitz metric, to functions of polynomial growth. Specifically, we prove that the DKSD controls the integral probability metric defined by a class of pseudo-Lipschitz functions, a polynomial generalization of Lipschitz functions. We also provide practical sufficient conditions on the reproducing kernel for the stated property to hold. In particular, we show that the DKSD detects non-convergence in moments with an appropriate kernel.

A kernel Stein test of goodness of fit for sequential models

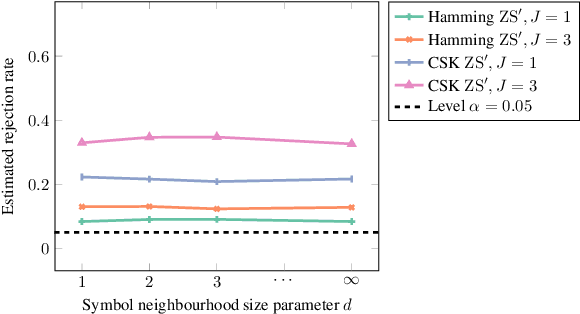
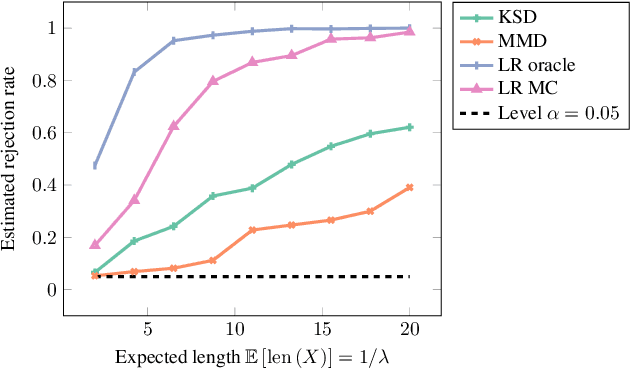
We propose a goodness-of-fit measure for probability densities modelling observations with varying dimensionality, such as text documents of differing lengths or variable-length sequences. The proposed measure is an instance of the kernel Stein discrepancy (KSD), which has been used to construct goodness-of-fit tests for unnormalised densities. Existing KSDs require the model to be defined on a fixed-dimension space. As our major contributions, we extend the KSD to the variable dimension setting by identifying appropriate Stein operators, and propose a novel KSD goodness-of-fit test. As with the previous variants, the proposed KSD does not require the density to be normalised, allowing the evaluation of a large class of models. Our test is shown to perform well in practice on discrete sequential data benchmarks.

Deep Proxy Causal Learning and its Application to Confounded Bandit Policy Evaluation

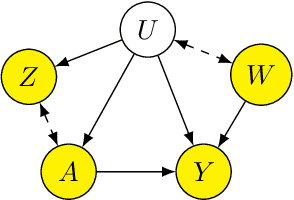
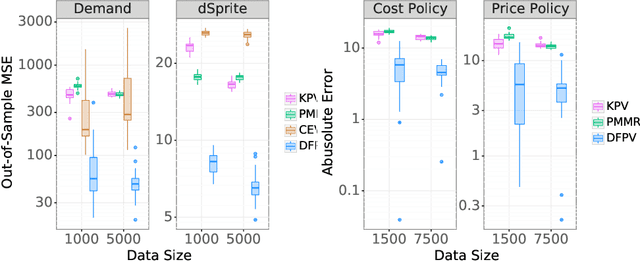
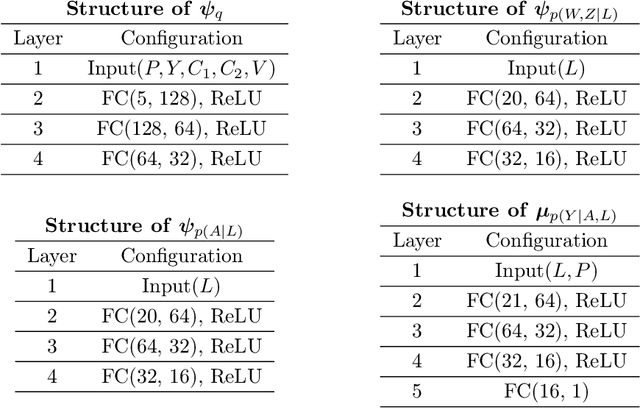
Proxy causal learning (PCL) is a method for estimating the causal effect of treatments on outcomes in the presence of unobserved confounding, using proxies (structured side information) for the confounder. This is achieved via two-stage regression: in the first stage, we model relations among the treatment and proxies; in the second stage, we use this model to learn the effect of treatment on the outcome, given the context provided by the proxies. PCL guarantees recovery of the true causal effect, subject to identifiability conditions. We propose a novel method for PCL, the deep feature proxy variable method (DFPV), to address the case where the proxies, treatments, and outcomes are high-dimensional and have nonlinear complex relationships, as represented by deep neural network features. We show that DFPV outperforms recent state-of-the-art PCL methods on challenging synthetic benchmarks, including settings involving high dimensional image data. Furthermore, we show that PCL can be applied to off-policy evaluation for the confounded bandit problem, in which DFPV also exhibits competitive performance.

Testing Goodness of Fit of Conditional Density Models with Kernels

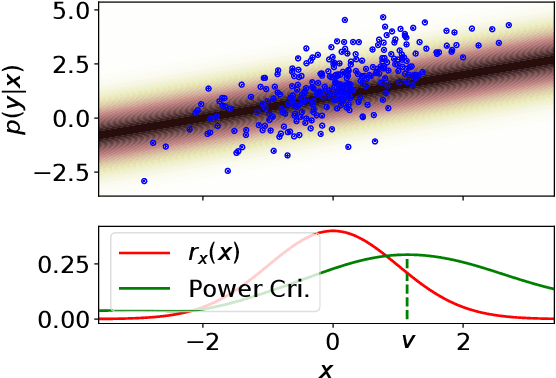
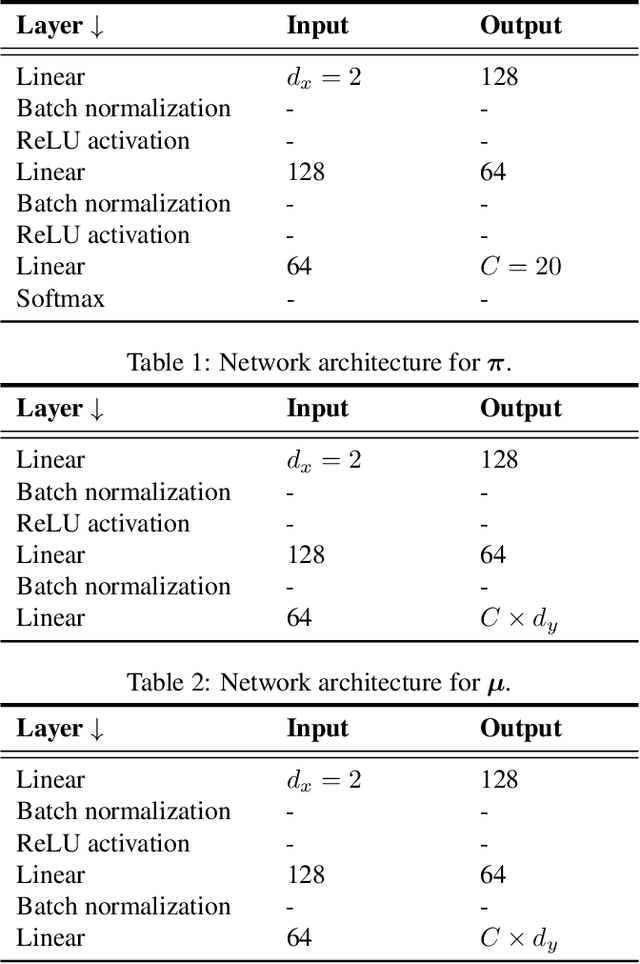
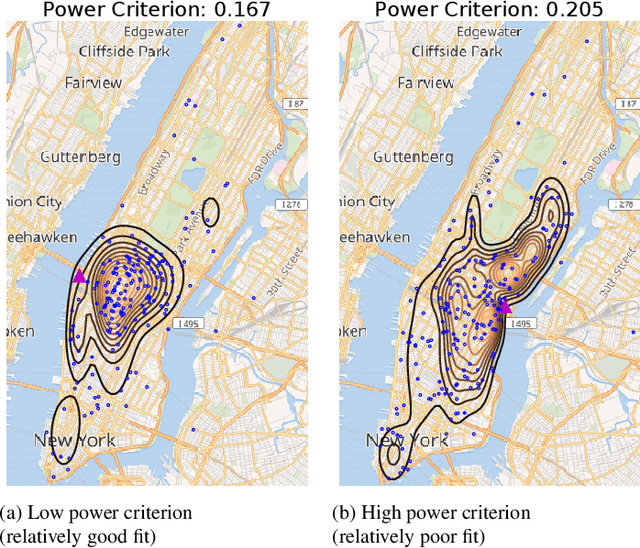
We propose two nonparametric statistical tests of goodness of fit for conditional distributions: given a conditional probability density function $p(y|x)$ and a joint sample, decide whether the sample is drawn from $p(y|x)r_x(x)$ for some density $r_x$. Our tests, formulated with a Stein operator, can be applied to any differentiable conditional density model, and require no knowledge of the normalizing constant. We show that 1) our tests are consistent against any fixed alternative conditional model; 2) the statistics can be estimated easily, requiring no density estimation as an intermediate step; and 3) our second test offers an interpretable test result providing insight on where the conditional model does not fit well in the domain of the covariate. We demonstrate the interpretability of our test on a task of modeling the distribution of New York City's taxi drop-off location given a pick-up point. To our knowledge, our work is the first to propose such conditional goodness-of-fit tests that simultaneously have all these desirable properties.

Amortised Learning by Wake-Sleep

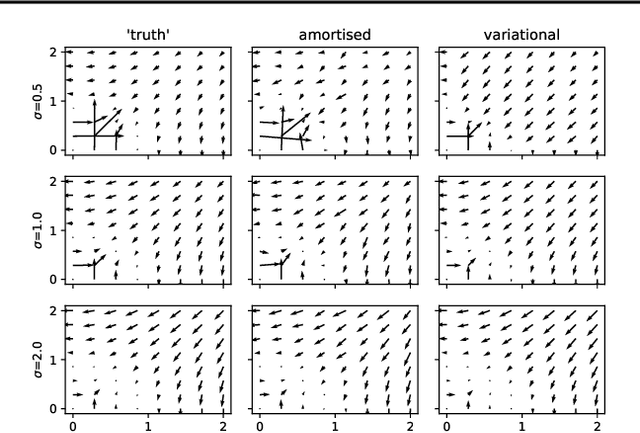
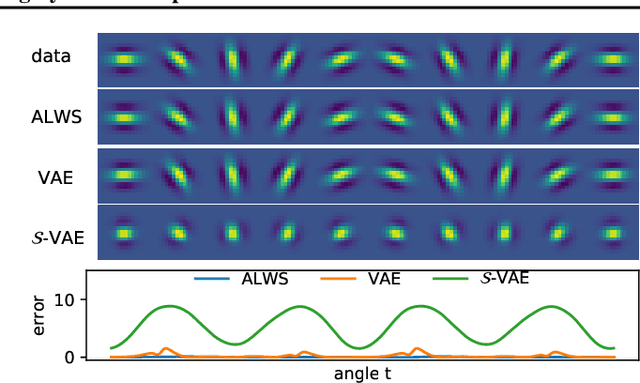
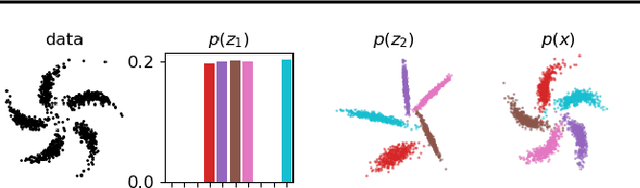
Models that employ latent variables to capture structure in observed data lie at the heart of many current unsupervised learning algorithms, but exact maximum-likelihood learning for powerful and flexible latent-variable models is almost always intractable. Thus, state-of-the-art approaches either abandon the maximum-likelihood framework entirely, or else rely on a variety of variational approximations to the posterior distribution over the latents. Here, we propose an alternative approach that we call amortised learning. Rather than computing an approximation to the posterior over latents, we use a wake-sleep Monte-Carlo strategy to learn a function that directly estimates the maximum-likelihood parameter updates. Amortised learning is possible whenever samples of latents and observations can be simulated from the generative model, treating the model as a "black box". We demonstrate its effectiveness on a wide range of complex models, including those with latents that are discrete or supported on non-Euclidean spaces.

A Kernel Stein Test for Comparing Latent Variable Models

We propose a nonparametric, kernel-based test to assess the relative goodness of fit of latent variable models with intractable unnormalized densities. Our test generalises the kernel Stein discrepancy (KSD) tests of (Liu et al., 2016, Chwialkowski et al., 2016, Yang et al., 2018, Jitkrittum et al., 2018) which required exact access to unnormalized densities. Our new test relies on the simple idea of using an approximate observed-variable marginal in place of the exact, intractable one. As our main theoretical contribution, we prove that the new test, with a properly corrected threshold, has a well-controlled type-I error. In the case of models with low-dimensional latent structure and high-dimensional observations, our test significantly outperforms the relative maximum mean discrepancy test (Bounliphone et al., 2015) , which cannot exploit the latent structure.

Informative Features for Model Comparison

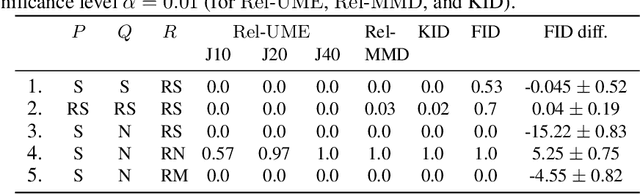
Given two candidate models, and a set of target observations, we address the problem of measuring the relative goodness of fit of the two models. We propose two new statistical tests which are nonparametric, computationally efficient (runtime complexity is linear in the sample size), and interpretable. As a unique advantage, our tests can produce a set of examples (informative features) indicating the regions in the data domain where one model fits significantly better than the other. In a real-world problem of comparing GAN models, the test power of our new test matches that of the state-of-the-art test of relative goodness of fit, while being one order of magnitude faster.

Cross-domain Recommendation via Deep Domain Adaptation

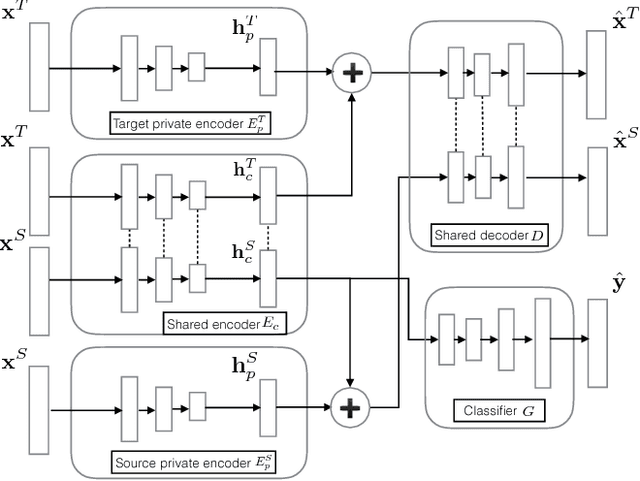
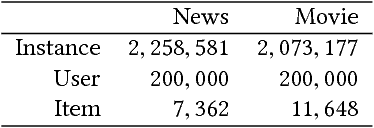
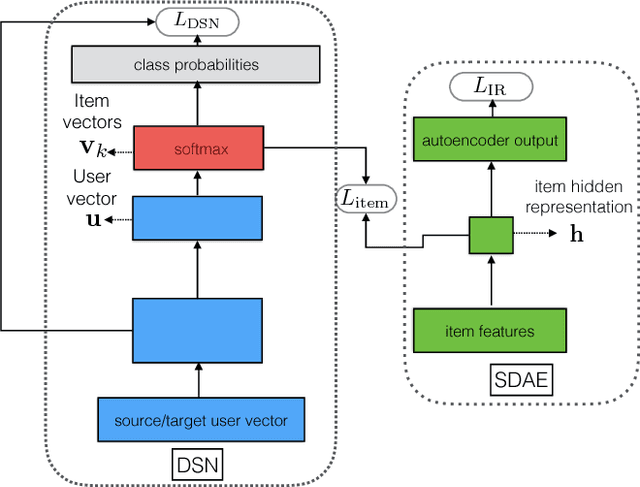
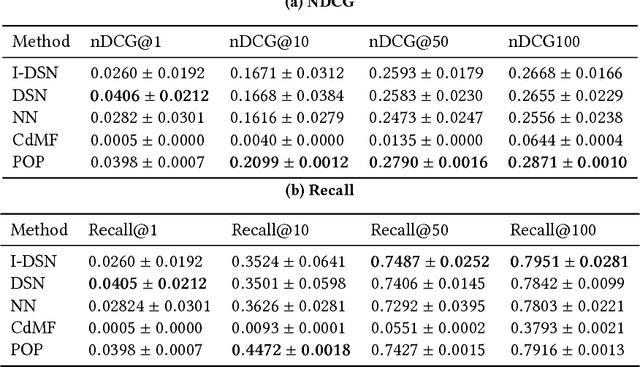
The behavior of users in certain services could be a clue that can be used to infer their preferences and may be used to make recommendations for other services they have never used. However, the cross-domain relationships between items and user consumption patterns are not simple, especially when there are few or no common users and items across domains. To address this problem, we propose a content-based cross-domain recommendation method for cold-start users that does not require user- and item- overlap. We formulate recommendation as extreme multi-class classification where labels (items) corresponding to the users are predicted. With this formulation, the problem is reduced to a domain adaptation setting, in which a classifier trained in the source domain is adapted to the target domain. For this, we construct a neural network that combines an architecture for domain adaptation, Domain Separation Network, with a denoising autoencoder for item representation. We assess the performance of our approach in experiments on a pair of data sets collected from movie and news services of Yahoo! JAPAN and show that our approach outperforms several baseline methods including a cross-domain collaborative filtering method.