Blindness of score-based methods to isolated components and mixing proportions

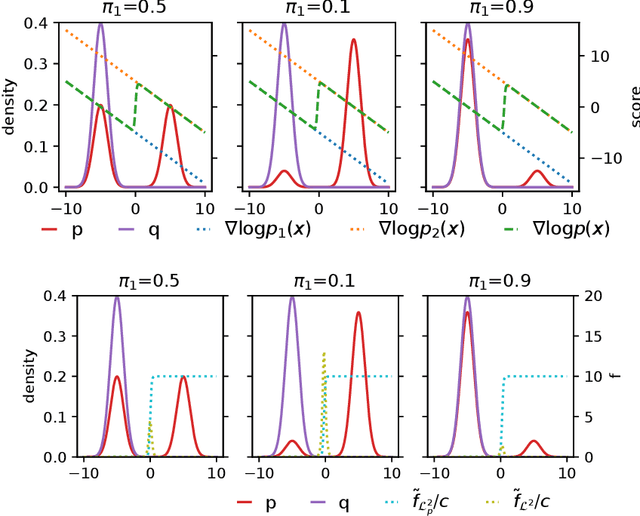
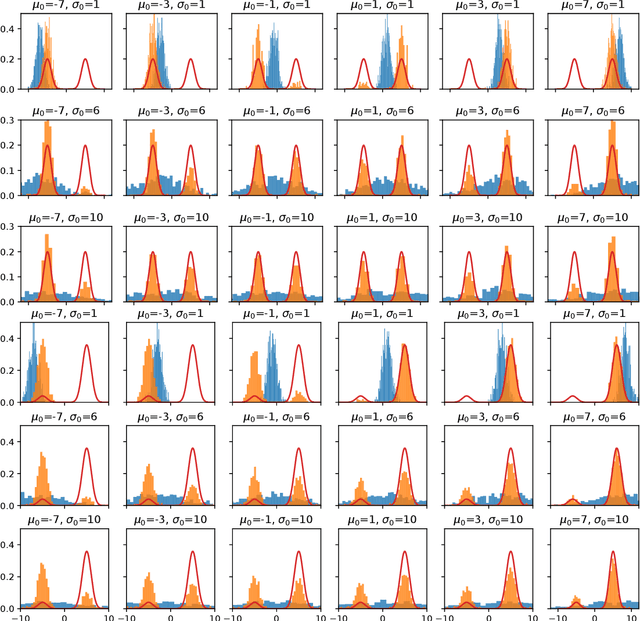
A large family of score-based methods are developed recently to solve unsupervised learning problems including density estimation, statistical testing and variational inference. These methods are attractive because they exploit the derivative of the log density, which is independent of the normaliser, and are thus suitable for tasks involving unnormalised densities. Despite the theoretical guarantees on the performance, here we illustrate a common practical issue suffered by these methods when the unnormalised distribution of interest has isolated components. In particular, we study the behaviour of some popular score-based methods on tasks involving 1-D mixture of Gaussian. These methods fail to identify appropriate mixing proportions when the unnormalised distribution is multimodal. Finally, some directions for finding a remedy are discussed in light of recent successes in specific tasks. We hope to bring the attention of theoreticians and practitioners to this issue when developing new algorithms and applications.

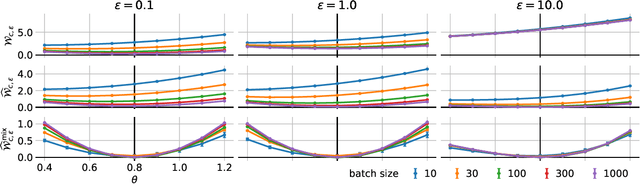
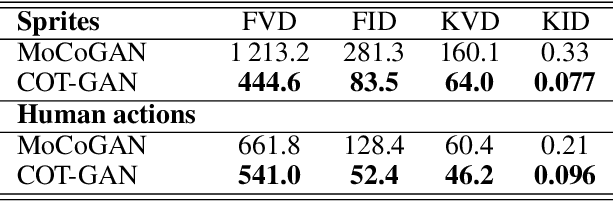
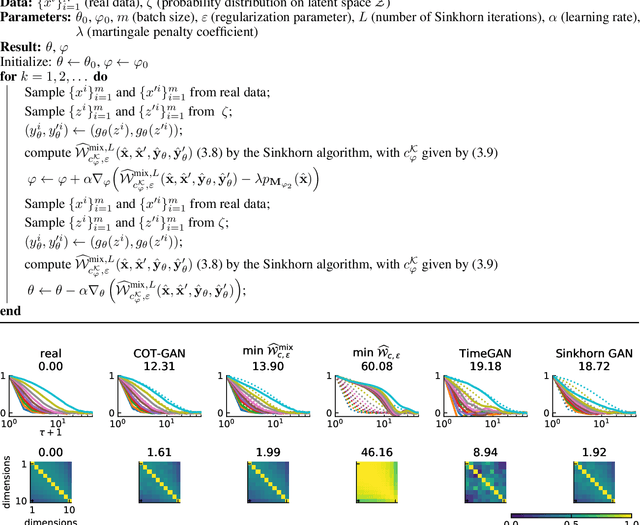
COT-GAN: Generating Sequential Data via Causal Optimal Transport

We introduce COT-GAN, an adversarial algorithm to train implicit generative models optimized for producing sequential data. The loss function of this algorithm is formulated using ideas from Causal Optimal Transport (COT), which combines classic optimal transport methods with an additional temporal causality constraint. Remarkably, we find that this causality condition provides a natural framework to parameterize the cost function that is learned by the discriminator as a robust (worst-case) distance, and an ideal mechanism for learning time dependent data distributions. Following Genevay et al.\ (2018), we also include an entropic penalization term which allows for the use of the Sinkhorn algorithm when computing the optimal transport cost. Our experiments show effectiveness and stability of COT-GAN when generating both low- and high-dimensional time series data. The success of the algorithm also relies on a new, improved version of the Sinkhorn divergence which demonstrates less bias in learning.

Amortised Learning by Wake-Sleep

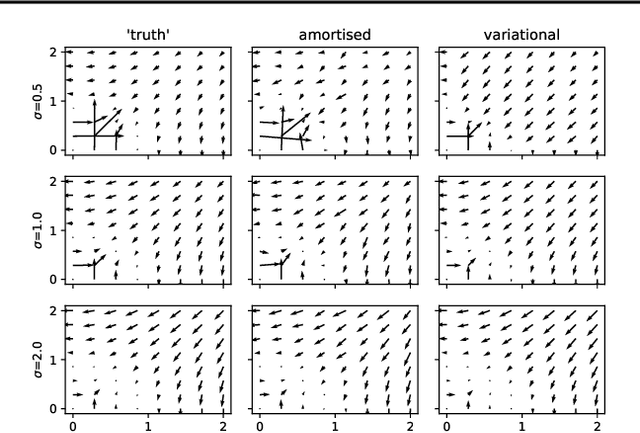
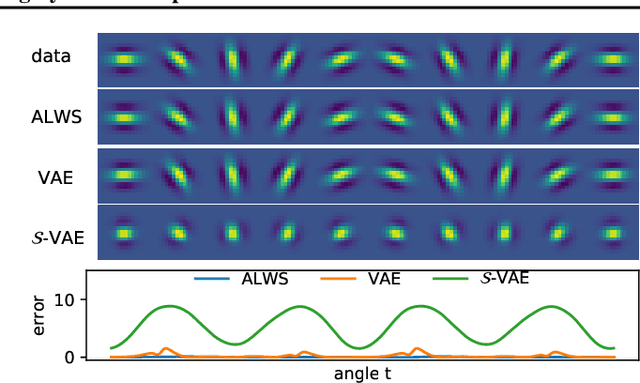
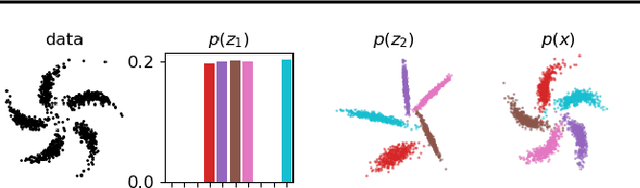
Models that employ latent variables to capture structure in observed data lie at the heart of many current unsupervised learning algorithms, but exact maximum-likelihood learning for powerful and flexible latent-variable models is almost always intractable. Thus, state-of-the-art approaches either abandon the maximum-likelihood framework entirely, or else rely on a variety of variational approximations to the posterior distribution over the latents. Here, we propose an alternative approach that we call amortised learning. Rather than computing an approximation to the posterior over latents, we use a wake-sleep Monte-Carlo strategy to learn a function that directly estimates the maximum-likelihood parameter updates. Amortised learning is possible whenever samples of latents and observations can be simulated from the generative model, treating the model as a "black box". We demonstrate its effectiveness on a wide range of complex models, including those with latents that are discrete or supported on non-Euclidean spaces.