Leveraging free energy in pretraining model selection for improved fine-tuning

Recent advances in artificial intelligence have been fueled by the development of foundation models such as BERT, GPT, T5, and Vision Transformers. These models are first pretrained on vast and diverse datasets and then adapted to specific downstream tasks, often with significantly less data. However, the mechanisms behind the success of this ubiquitous pretrain-then-adapt paradigm remain underexplored, particularly the characteristics of pretraining checkpoints that lend themselves to good downstream adaptation. We introduce a Bayesian model selection criterion, called the downstream free energy, which quantifies a checkpoint's adaptability by measuring the concentration of nearby favorable parameters for the downstream task. We demonstrate that this free energy criterion can be effectively implemented without access to the downstream data or prior knowledge of the downstream task. Furthermore, we provide empirical evidence that the free energy criterion reliably correlates with improved fine-tuning performance, offering a principled approach to predicting model adaptability.

The Impact of Geometric Complexity on Neural Collapse in Transfer Learning

Many of the recent remarkable advances in computer vision and language models can be attributed to the success of transfer learning via the pre-training of large foundation models. However, a theoretical framework which explains this empirical success is incomplete and remains an active area of research. Flatness of the loss surface and neural collapse have recently emerged as useful pre-training metrics which shed light on the implicit biases underlying pre-training. In this paper, we explore the geometric complexity of a model's learned representations as a fundamental mechanism that relates these two concepts. We show through experiments and theory that mechanisms which affect the geometric complexity of the pre-trained network also influence the neural collapse. Furthermore, we show how this effect of the geometric complexity generalizes to the neural collapse of new classes as well, thus encouraging better performance on downstream tasks, particularly in the few-shot setting.

A Margin-based Multiclass Generalization Bound via Geometric Complexity

There has been considerable effort to better understand the generalization capabilities of deep neural networks both as a means to unlock a theoretical understanding of their success as well as providing directions for further improvements. In this paper, we investigate margin-based multiclass generalization bounds for neural networks which rely on a recent complexity measure, the geometric complexity, developed for neural networks. We derive a new upper bound on the generalization error which scales with the margin-normalized geometric complexity of the network and which holds for a broad family of data distributions and model classes. Our generalization bound is empirically investigated for a ResNet-18 model trained with SGD on the CIFAR-10 and CIFAR-100 datasets with both original and random labels.

Unified Functional Hashing in Automatic Machine Learning

The field of Automatic Machine Learning (AutoML) has recently attained impressive results, including the discovery of state-of-the-art machine learning solutions, such as neural image classifiers. This is often done by applying an evolutionary search method, which samples multiple candidate solutions from a large space and evaluates the quality of each candidate through a long training process. As a result, the search tends to be slow. In this paper, we show that large efficiency gains can be obtained by employing a fast unified functional hash, especially through the functional equivalence caching technique, which we also present. The central idea is to detect by hashing when the search method produces equivalent candidates, which occurs very frequently, and this way avoid their costly re-evaluation. Our hash is "functional" in that it identifies equivalent candidates even if they were represented or coded differently, and it is "unified" in that the same algorithm can hash arbitrary representations; e.g. compute graphs, imperative code, or lambda functions. As evidence, we show dramatic improvements on multiple AutoML domains, including neural architecture search and algorithm discovery. Finally, we consider the effect of hash collisions, evaluation noise, and search distribution through empirical analysis. Altogether, we hope this paper may serve as a guide to hashing techniques in AutoML.

Why neural networks find simple solutions: the many regularizers of geometric complexity

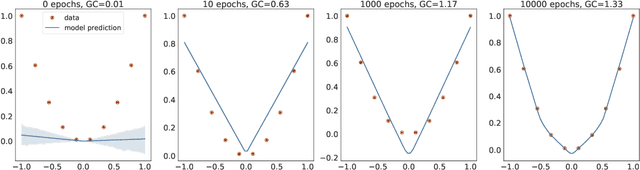
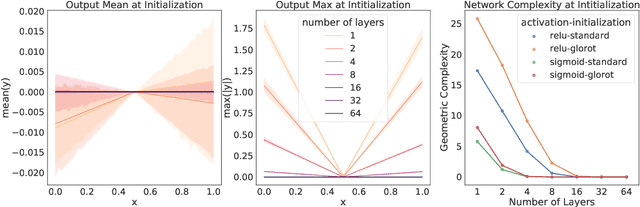
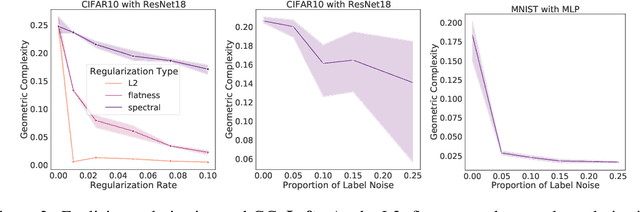
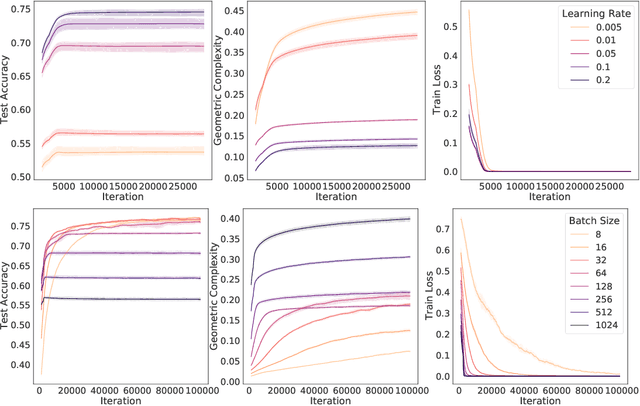
In many contexts, simpler models are preferable to more complex models and the control of this model complexity is the goal for many methods in machine learning such as regularization, hyperparameter tuning and architecture design. In deep learning, it has been difficult to understand the underlying mechanisms of complexity control, since many traditional measures are not naturally suitable for deep neural networks. Here we develop the notion of geometric complexity, which is a measure of the variability of the model function, computed using a discrete Dirichlet energy. Using a combination of theoretical arguments and empirical results, we show that many common training heuristics such as parameter norm regularization, spectral norm regularization, flatness regularization, implicit gradient regularization, noise regularization and the choice of parameter initialization all act to control geometric complexity, providing a unifying framework in which to characterize the behavior of deep learning models.

The Geometric Occam's Razor Implicit in Deep Learning

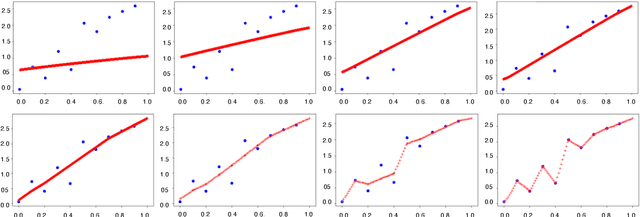
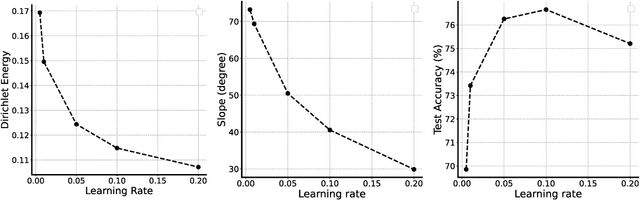
In over-parameterized deep neural networks there can be many possible parameter configurations that fit the training data exactly. However, the properties of these interpolating solutions are poorly understood. We argue that over-parameterized neural networks trained with stochastic gradient descent are subject to a Geometric Occam's Razor; that is, these networks are implicitly regularized by the geometric model complexity. For one-dimensional regression, the geometric model complexity is simply given by the arc length of the function. For higher-dimensional settings, the geometric model complexity depends on the Dirichlet energy of the function. We explore the relationship between this Geometric Occam's Razor, the Dirichlet energy and other known forms of implicit regularization. Finally, for ResNets trained on CIFAR-10, we observe that Dirichlet energy measurements are consistent with the action of this implicit Geometric Occam's Razor.

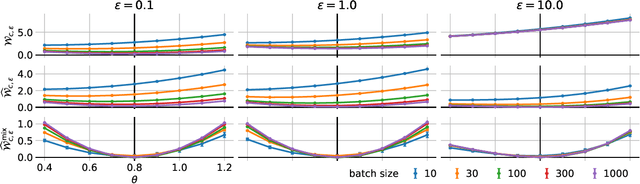
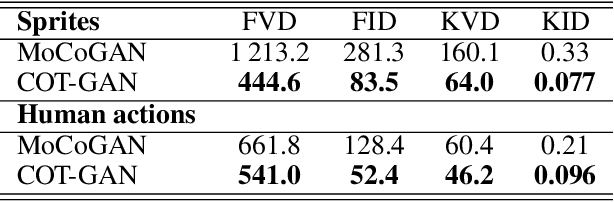
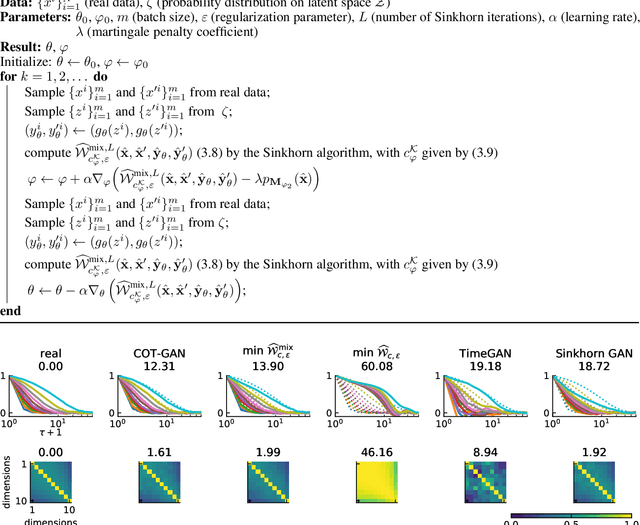
COT-GAN: Generating Sequential Data via Causal Optimal Transport

We introduce COT-GAN, an adversarial algorithm to train implicit generative models optimized for producing sequential data. The loss function of this algorithm is formulated using ideas from Causal Optimal Transport (COT), which combines classic optimal transport methods with an additional temporal causality constraint. Remarkably, we find that this causality condition provides a natural framework to parameterize the cost function that is learned by the discriminator as a robust (worst-case) distance, and an ideal mechanism for learning time dependent data distributions. Following Genevay et al.\ (2018), we also include an entropic penalization term which allows for the use of the Sinkhorn algorithm when computing the optimal transport cost. Our experiments show effectiveness and stability of COT-GAN when generating both low- and high-dimensional time series data. The success of the algorithm also relies on a new, improved version of the Sinkhorn divergence which demonstrates less bias in learning.