The Impact of Geometric Complexity on Neural Collapse in Transfer Learning

Many of the recent remarkable advances in computer vision and language models can be attributed to the success of transfer learning via the pre-training of large foundation models. However, a theoretical framework which explains this empirical success is incomplete and remains an active area of research. Flatness of the loss surface and neural collapse have recently emerged as useful pre-training metrics which shed light on the implicit biases underlying pre-training. In this paper, we explore the geometric complexity of a model's learned representations as a fundamental mechanism that relates these two concepts. We show through experiments and theory that mechanisms which affect the geometric complexity of the pre-trained network also influence the neural collapse. Furthermore, we show how this effect of the geometric complexity generalizes to the neural collapse of new classes as well, thus encouraging better performance on downstream tasks, particularly in the few-shot setting.

A Margin-based Multiclass Generalization Bound via Geometric Complexity

There has been considerable effort to better understand the generalization capabilities of deep neural networks both as a means to unlock a theoretical understanding of their success as well as providing directions for further improvements. In this paper, we investigate margin-based multiclass generalization bounds for neural networks which rely on a recent complexity measure, the geometric complexity, developed for neural networks. We derive a new upper bound on the generalization error which scales with the margin-normalized geometric complexity of the network and which holds for a broad family of data distributions and model classes. Our generalization bound is empirically investigated for a ResNet-18 model trained with SGD on the CIFAR-10 and CIFAR-100 datasets with both original and random labels.

Corridor Geometry in Gradient-Based Optimization

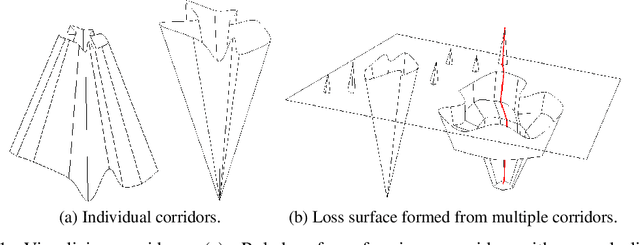
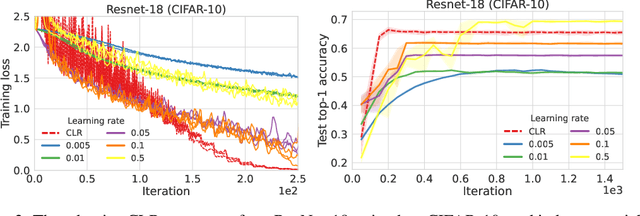
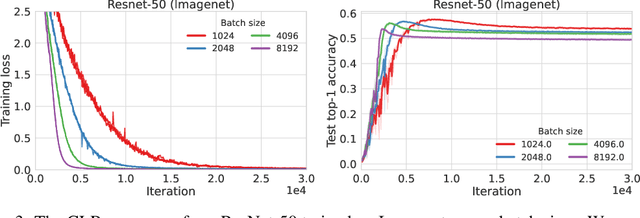
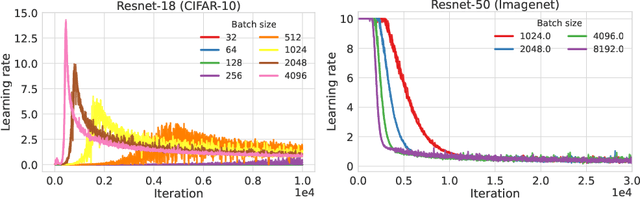
We characterize regions of a loss surface as corridors when the continuous curves of steepest descent -- the solutions of the gradient flow -- become straight lines. We show that corridors provide insights into gradient-based optimization, since corridors are exactly the regions where gradient descent and the gradient flow follow the same trajectory, while the loss decreases linearly. As a result, inside corridors there are no implicit regularization effects or training instabilities that have been shown to occur due to the drift between gradient descent and the gradient flow. Using the loss linear decrease on corridors, we devise a learning rate adaptation scheme for gradient descent; we call this scheme Corridor Learning Rate (CLR). The CLR formulation coincides with a special case of Polyak step-size, discovered in the context of convex optimization. The Polyak step-size has been shown recently to have also good convergence properties for neural networks; we further confirm this here with results on CIFAR-10 and ImageNet.

Implicit biases in multitask and continual learning from a backward error analysis perspective

Using backward error analysis, we compute implicit training biases in multitask and continual learning settings for neural networks trained with stochastic gradient descent. In particular, we derive modified losses that are implicitly minimized during training. They have three terms: the original loss, accounting for convergence, an implicit flatness regularization term proportional to the learning rate, and a last term, the conflict term, which can theoretically be detrimental to both convergence and implicit regularization. In multitask, the conflict term is a well-known quantity, measuring the gradient alignment between the tasks, while in continual learning the conflict term is a new quantity in deep learning optimization, although a basic tool in differential geometry: The Lie bracket between the task gradients.

Morse Neural Networks for Uncertainty Quantification

We introduce a new deep generative model useful for uncertainty quantification: the Morse neural network, which generalizes the unnormalized Gaussian densities to have modes of high-dimensional submanifolds instead of just discrete points. Fitting the Morse neural network via a KL-divergence loss yields 1) a (unnormalized) generative density, 2) an OOD detector, 3) a calibration temperature, 4) a generative sampler, along with in the supervised case 5) a distance aware-classifier. The Morse network can be used on top of a pre-trained network to bring distance-aware calibration w.r.t the training data. Because of its versatility, the Morse neural networks unifies many techniques: e.g., the Entropic Out-of-Distribution Detector of (Mac\^edo et al., 2021) in OOD detection, the one class Deep Support Vector Description method of (Ruff et al., 2018) in anomaly detection, or the Contrastive One Class classifier in continuous learning (Sun et al., 2021). The Morse neural network has connections to support vector machines, kernel methods, and Morse theory in topology.

On a continuous time model of gradient descent dynamics and instability in deep learning

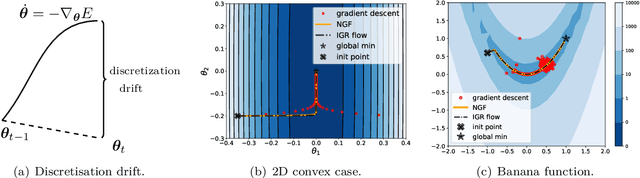
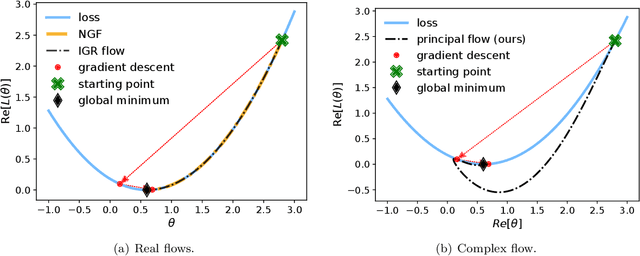
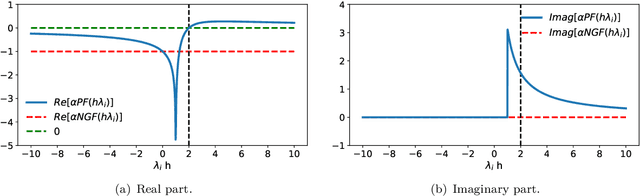
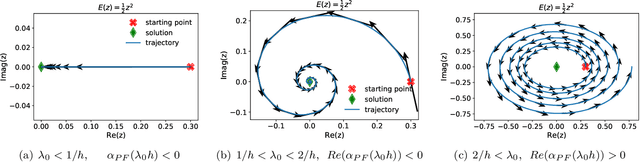
The recipe behind the success of deep learning has been the combination of neural networks and gradient-based optimization. Understanding the behavior of gradient descent however, and particularly its instability, has lagged behind its empirical success. To add to the theoretical tools available to study gradient descent we propose the principal flow (PF), a continuous time flow that approximates gradient descent dynamics. To our knowledge, the PF is the only continuous flow that captures the divergent and oscillatory behaviors of gradient descent, including escaping local minima and saddle points. Through its dependence on the eigendecomposition of the Hessian the PF sheds light on the recently observed edge of stability phenomena in deep learning. Using our new understanding of instability we propose a learning rate adaptation method which enables us to control the trade-off between training stability and test set evaluation performance.

Why neural networks find simple solutions: the many regularizers of geometric complexity

In many contexts, simpler models are preferable to more complex models and the control of this model complexity is the goal for many methods in machine learning such as regularization, hyperparameter tuning and architecture design. In deep learning, it has been difficult to understand the underlying mechanisms of complexity control, since many traditional measures are not naturally suitable for deep neural networks. Here we develop the notion of geometric complexity, which is a measure of the variability of the model function, computed using a discrete Dirichlet energy. Using a combination of theoretical arguments and empirical results, we show that many common training heuristics such as parameter norm regularization, spectral norm regularization, flatness regularization, implicit gradient regularization, noise regularization and the choice of parameter initialization all act to control geometric complexity, providing a unifying framework in which to characterize the behavior of deep learning models.

The Geometric Occam's Razor Implicit in Deep Learning

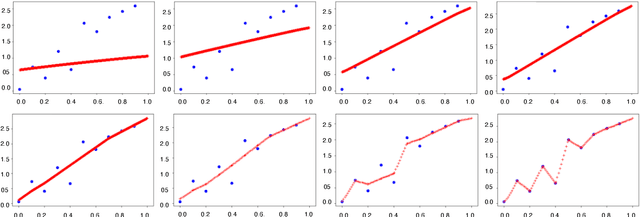
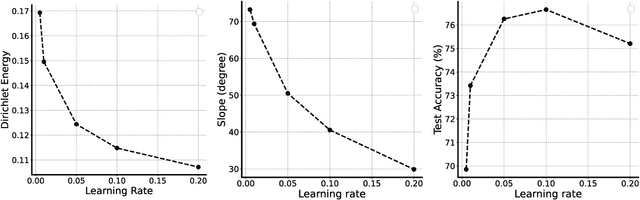
In over-parameterized deep neural networks there can be many possible parameter configurations that fit the training data exactly. However, the properties of these interpolating solutions are poorly understood. We argue that over-parameterized neural networks trained with stochastic gradient descent are subject to a Geometric Occam's Razor; that is, these networks are implicitly regularized by the geometric model complexity. For one-dimensional regression, the geometric model complexity is simply given by the arc length of the function. For higher-dimensional settings, the geometric model complexity depends on the Dirichlet energy of the function. We explore the relationship between this Geometric Occam's Razor, the Dirichlet energy and other known forms of implicit regularization. Finally, for ResNets trained on CIFAR-10, we observe that Dirichlet energy measurements are consistent with the action of this implicit Geometric Occam's Razor.

Discretization Drift in Two-Player Games

Gradient-based methods for two-player games produce rich dynamics that can solve challenging problems, yet can be difficult to stabilize and understand. Part of this complexity originates from the discrete update steps given by simultaneous or alternating gradient descent, which causes each player to drift away from the continuous gradient flow -- a phenomenon we call discretization drift. Using backward error analysis, we derive modified continuous dynamical systems that closely follow the discrete dynamics. These modified dynamics provide an insight into the notorious challenges associated with zero-sum games, including Generative Adversarial Networks. In particular, we identify distinct components of the discretization drift that can alter performance and in some cases destabilize the game. Finally, quantifying discretization drift allows us to identify regularizers that explicitly cancel harmful forms of drift or strengthen beneficial forms of drift, and thus improve performance of GAN training.

On the Origin of Implicit Regularization in Stochastic Gradient Descent

For infinitesimal learning rates, stochastic gradient descent (SGD) follows the path of gradient flow on the full batch loss function. However moderately large learning rates can achieve higher test accuracies, and this generalization benefit is not explained by convergence bounds, since the learning rate which maximizes test accuracy is often larger than the learning rate which minimizes training loss. To interpret this phenomenon we prove that for SGD with random shuffling, the mean SGD iterate also stays close to the path of gradient flow if the learning rate is small and finite, but on a modified loss. This modified loss is composed of the original loss function and an implicit regularizer, which penalizes the norms of the minibatch gradients. Under mild assumptions, when the batch size is small the scale of the implicit regularization term is proportional to the ratio of the learning rate to the batch size. We verify empirically that explicitly including the implicit regularizer in the loss can enhance the test accuracy when the learning rate is small.