Corridor Geometry in Gradient-Based Optimization
Paper and Code
Feb 13, 2024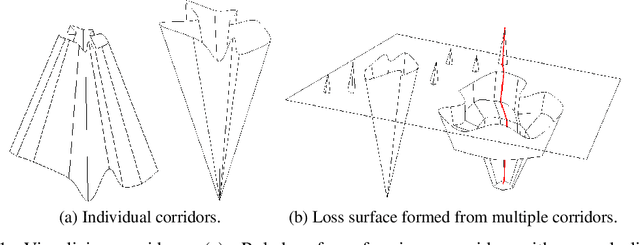
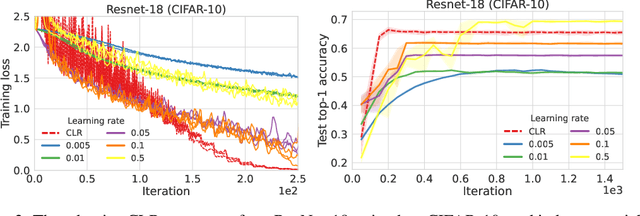
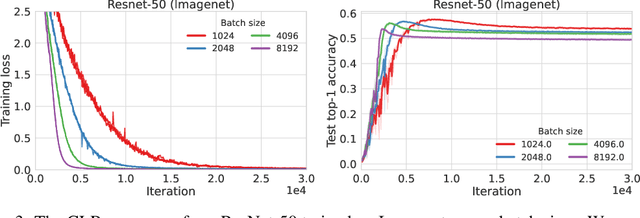
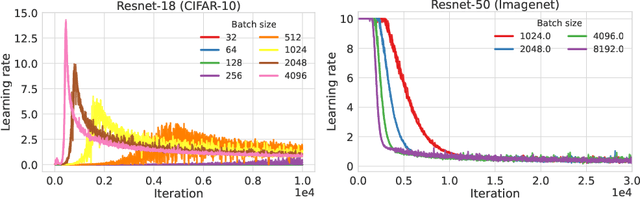
We characterize regions of a loss surface as corridors when the continuous curves of steepest descent -- the solutions of the gradient flow -- become straight lines. We show that corridors provide insights into gradient-based optimization, since corridors are exactly the regions where gradient descent and the gradient flow follow the same trajectory, while the loss decreases linearly. As a result, inside corridors there are no implicit regularization effects or training instabilities that have been shown to occur due to the drift between gradient descent and the gradient flow. Using the loss linear decrease on corridors, we devise a learning rate adaptation scheme for gradient descent; we call this scheme Corridor Learning Rate (CLR). The CLR formulation coincides with a special case of Polyak step-size, discovered in the context of convex optimization. The Polyak step-size has been shown recently to have also good convergence properties for neural networks; we further confirm this here with results on CIFAR-10 and ImageNet.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge