Neural Compression of Atmospheric States

Atmospheric states derived from reanalysis comprise a substantial portion of weather and climate simulation outputs. Many stakeholders -- such as researchers, policy makers, and insurers -- use this data to better understand the earth system and guide policy decisions. Atmospheric states have also received increased interest as machine learning approaches to weather prediction have shown promising results. A key issue for all audiences is that dense time series of these high-dimensional states comprise an enormous amount of data, precluding all but the most well resourced groups from accessing and using historical data and future projections. To address this problem, we propose a method for compressing atmospheric states using methods from the neural network literature, adapting spherical data to processing by conventional neural architectures through the use of the area-preserving HEALPix projection. We investigate two model classes for building neural compressors: the hyperprior model from the neural image compression literature and recent vector-quantised models. We show that both families of models satisfy the desiderata of small average error, a small number of high-error reconstructed pixels, faithful reproduction of extreme events such as hurricanes and heatwaves, preservation of the spectral power distribution across spatial scales. We demonstrate compression ratios in excess of 1000x, with compression and decompression at a rate of approximately one second per global atmospheric state.

Gemini 1.5: Unlocking multimodal understanding across millions of tokens of context

In this report, we present the latest model of the Gemini family, Gemini 1.5 Pro, a highly compute-efficient multimodal mixture-of-experts model capable of recalling and reasoning over fine-grained information from millions of tokens of context, including multiple long documents and hours of video and audio. Gemini 1.5 Pro achieves near-perfect recall on long-context retrieval tasks across modalities, improves the state-of-the-art in long-document QA, long-video QA and long-context ASR, and matches or surpasses Gemini 1.0 Ultra's state-of-the-art performance across a broad set of benchmarks. Studying the limits of Gemini 1.5 Pro's long-context ability, we find continued improvement in next-token prediction and near-perfect retrieval (>99%) up to at least 10M tokens, a generational leap over existing models such as Claude 2.1 (200k) and GPT-4 Turbo (128k). Finally, we highlight surprising new capabilities of large language models at the frontier; when given a grammar manual for Kalamang, a language with fewer than 200 speakers worldwide, the model learns to translate English to Kalamang at a similar level to a person who learned from the same content.

Corridor Geometry in Gradient-Based Optimization

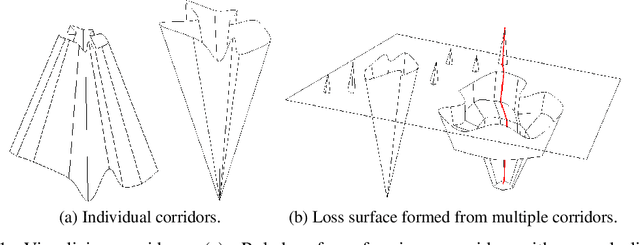
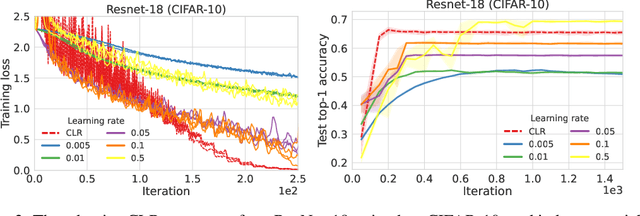
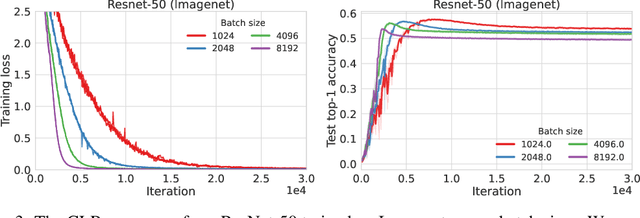
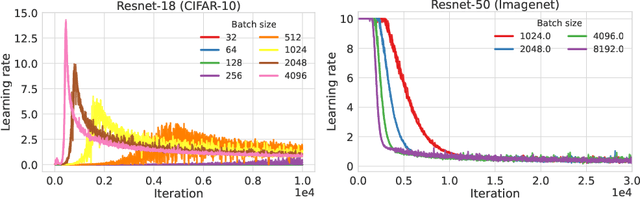
We characterize regions of a loss surface as corridors when the continuous curves of steepest descent -- the solutions of the gradient flow -- become straight lines. We show that corridors provide insights into gradient-based optimization, since corridors are exactly the regions where gradient descent and the gradient flow follow the same trajectory, while the loss decreases linearly. As a result, inside corridors there are no implicit regularization effects or training instabilities that have been shown to occur due to the drift between gradient descent and the gradient flow. Using the loss linear decrease on corridors, we devise a learning rate adaptation scheme for gradient descent; we call this scheme Corridor Learning Rate (CLR). The CLR formulation coincides with a special case of Polyak step-size, discovered in the context of convex optimization. The Polyak step-size has been shown recently to have also good convergence properties for neural networks; we further confirm this here with results on CIFAR-10 and ImageNet.

Implicit regularisation in stochastic gradient descent: from single-objective to two-player games

Recent years have seen many insights on deep learning optimisation being brought forward by finding implicit regularisation effects of commonly used gradient-based optimisers. Understanding implicit regularisation can not only shed light on optimisation dynamics, but it can also be used to improve performance and stability across problem domains, from supervised learning to two-player games such as Generative Adversarial Networks. An avenue for finding such implicit regularisation effects has been quantifying the discretisation errors of discrete optimisers via continuous-time flows constructed by backward error analysis (BEA). The current usage of BEA is not without limitations, since not all the vector fields of continuous-time flows obtained using BEA can be written as a gradient, hindering the construction of modified losses revealing implicit regularisers. In this work, we provide a novel approach to use BEA, and show how our approach can be used to construct continuous-time flows with vector fields that can be written as gradients. We then use this to find previously unknown implicit regularisation effects, such as those induced by multiple stochastic gradient descent steps while accounting for the exact data batches used in the updates, and in generally differentiable two-player games.

Investigating the Edge of Stability Phenomenon in Reinforcement Learning

Recent progress has been made in understanding optimisation dynamics in neural networks trained with full-batch gradient descent with momentum with the uncovering of the edge of stability phenomenon in supervised learning. The edge of stability phenomenon occurs as the leading eigenvalue of the Hessian reaches the divergence threshold of the underlying optimisation algorithm for a quadratic loss, after which it starts oscillating around the threshold, and the loss starts to exhibit local instability but decreases over long time frames. In this work, we explore the edge of stability phenomenon in reinforcement learning (RL), specifically off-policy Q-learning algorithms across a variety of data regimes, from offline to online RL. Our experiments reveal that, despite significant differences to supervised learning, such as non-stationarity of the data distribution and the use of bootstrapping, the edge of stability phenomenon can be present in off-policy deep RL. Unlike supervised learning, however, we observe strong differences depending on the underlying loss, with DQN -- using a Huber loss -- showing a strong edge of stability effect that we do not observe with C51 -- using a cross entropy loss. Our results suggest that, while neural network structure can lead to optimisation dynamics that transfer between problem domains, certain aspects of deep RL optimisation can differentiate it from domains such as supervised learning.

On a continuous time model of gradient descent dynamics and instability in deep learning

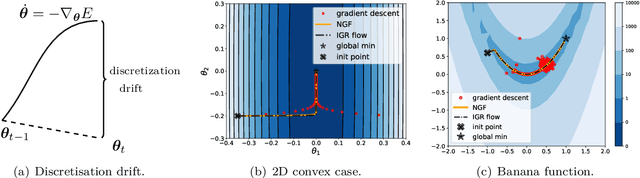
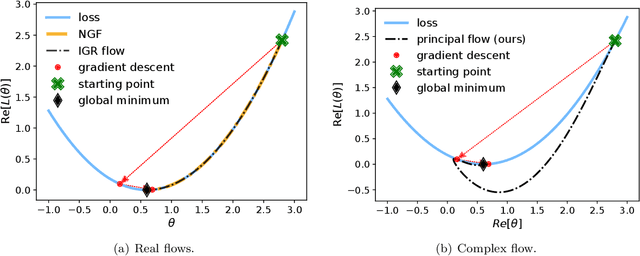
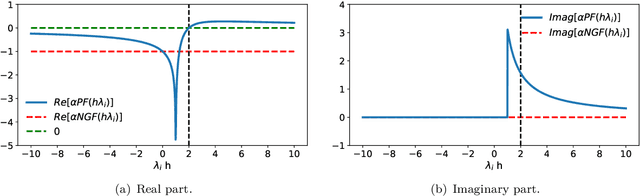
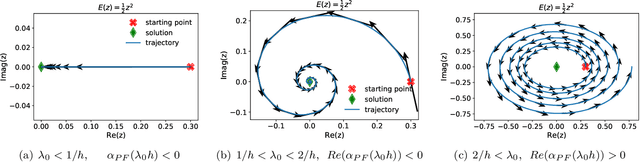
The recipe behind the success of deep learning has been the combination of neural networks and gradient-based optimization. Understanding the behavior of gradient descent however, and particularly its instability, has lagged behind its empirical success. To add to the theoretical tools available to study gradient descent we propose the principal flow (PF), a continuous time flow that approximates gradient descent dynamics. To our knowledge, the PF is the only continuous flow that captures the divergent and oscillatory behaviors of gradient descent, including escaping local minima and saddle points. Through its dependence on the eigendecomposition of the Hessian the PF sheds light on the recently observed edge of stability phenomena in deep learning. Using our new understanding of instability we propose a learning rate adaptation method which enables us to control the trade-off between training stability and test set evaluation performance.

Why neural networks find simple solutions: the many regularizers of geometric complexity

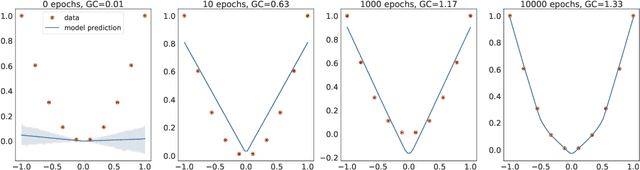
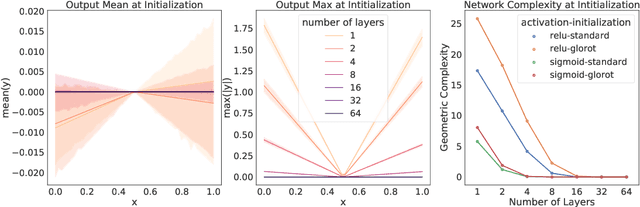
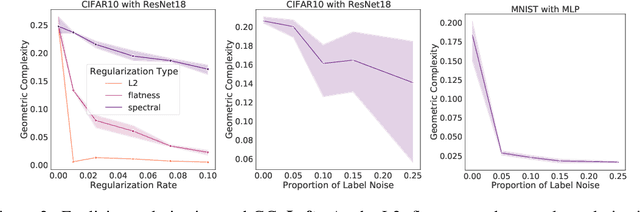
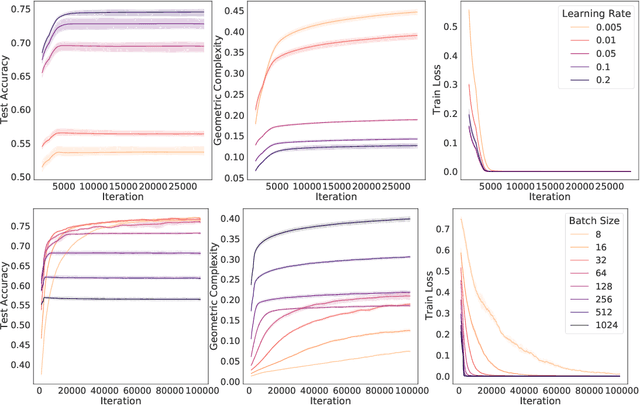
In many contexts, simpler models are preferable to more complex models and the control of this model complexity is the goal for many methods in machine learning such as regularization, hyperparameter tuning and architecture design. In deep learning, it has been difficult to understand the underlying mechanisms of complexity control, since many traditional measures are not naturally suitable for deep neural networks. Here we develop the notion of geometric complexity, which is a measure of the variability of the model function, computed using a discrete Dirichlet energy. Using a combination of theoretical arguments and empirical results, we show that many common training heuristics such as parameter norm regularization, spectral norm regularization, flatness regularization, implicit gradient regularization, noise regularization and the choice of parameter initialization all act to control geometric complexity, providing a unifying framework in which to characterize the behavior of deep learning models.

Discretization Drift in Two-Player Games

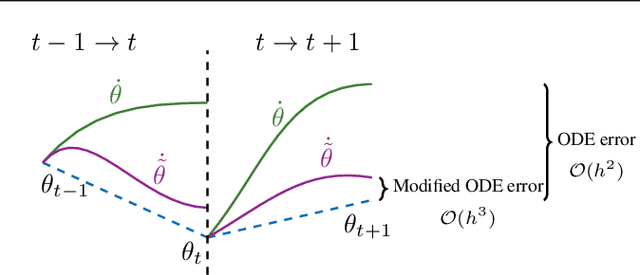
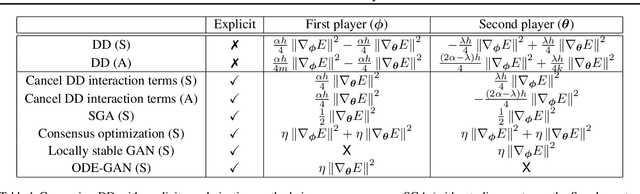
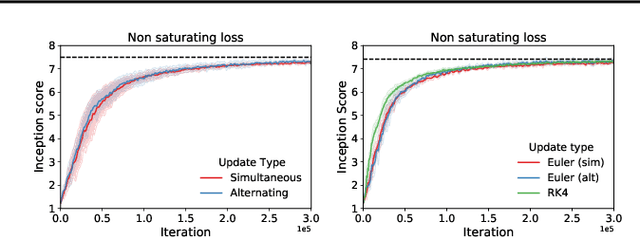
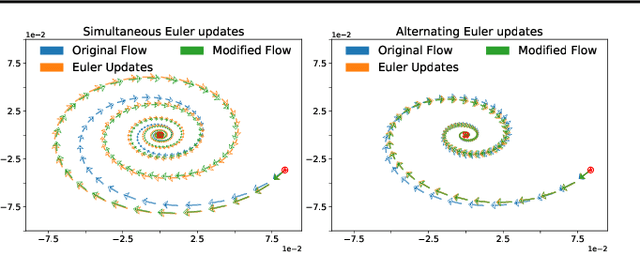
Gradient-based methods for two-player games produce rich dynamics that can solve challenging problems, yet can be difficult to stabilize and understand. Part of this complexity originates from the discrete update steps given by simultaneous or alternating gradient descent, which causes each player to drift away from the continuous gradient flow -- a phenomenon we call discretization drift. Using backward error analysis, we derive modified continuous dynamical systems that closely follow the discrete dynamics. These modified dynamics provide an insight into the notorious challenges associated with zero-sum games, including Generative Adversarial Networks. In particular, we identify distinct components of the discretization drift that can alter performance and in some cases destabilize the game. Finally, quantifying discretization drift allows us to identify regularizers that explicitly cancel harmful forms of drift or strengthen beneficial forms of drift, and thus improve performance of GAN training.

Spectral Normalisation for Deep Reinforcement Learning: an Optimisation Perspective

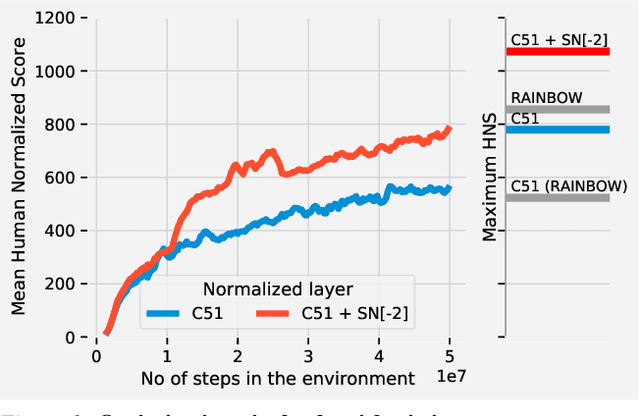
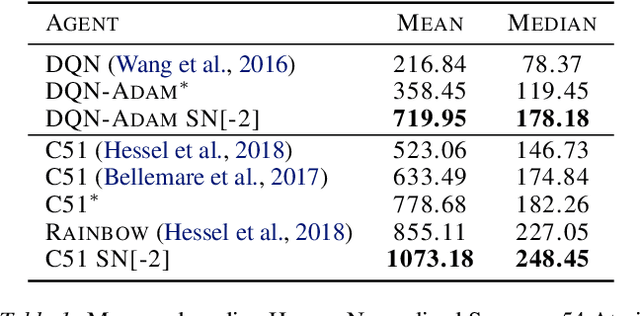
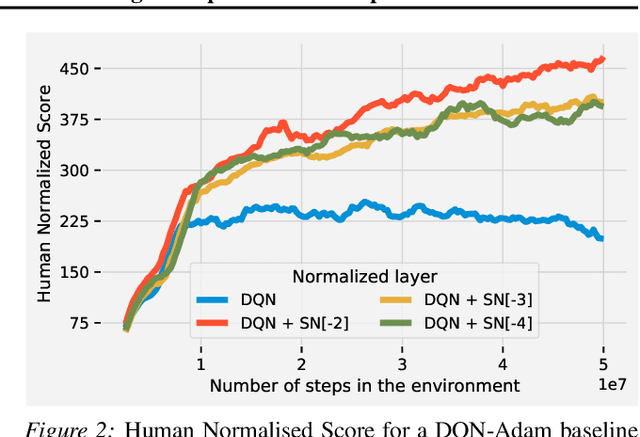
Most of the recent deep reinforcement learning advances take an RL-centric perspective and focus on refinements of the training objective. We diverge from this view and show we can recover the performance of these developments not by changing the objective, but by regularising the value-function estimator. Constraining the Lipschitz constant of a single layer using spectral normalisation is sufficient to elevate the performance of a Categorical-DQN agent to that of a more elaborated \rainbow{} agent on the challenging Atari domain. We conduct ablation studies to disentangle the various effects normalisation has on the learning dynamics and show that is sufficient to modulate the parameter updates to recover most of the performance of spectral normalisation. These findings hint towards the need to also focus on the neural component and its learning dynamics to tackle the peculiarities of Deep Reinforcement Learning.

A case for new neural network smoothness constraints

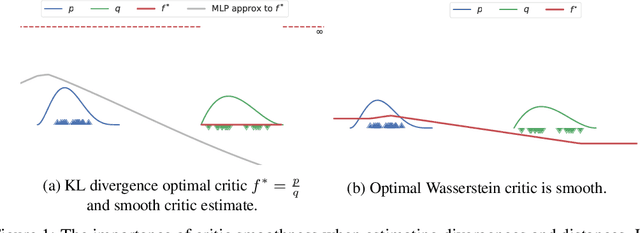
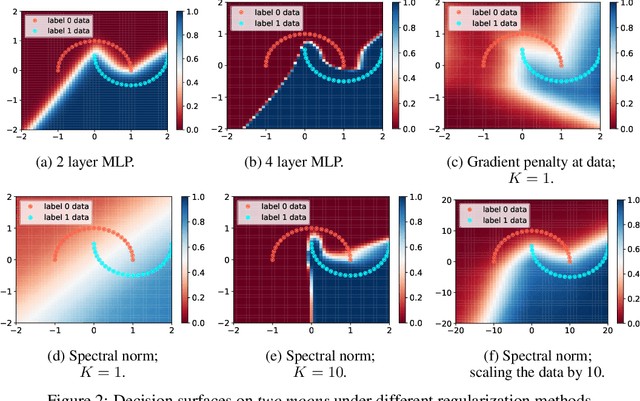
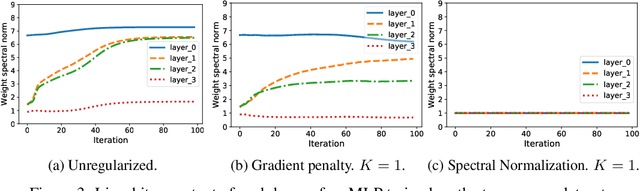
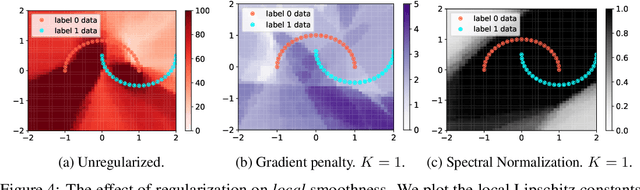
How sensitive should machine learning models be to input changes? We tackle the question of model smoothness and show that it is a useful inductive bias which aids generalization, adversarial robustness, generative modeling and reinforcement learning. We explore current methods of imposing smoothness constraints and observe they lack the flexibility to adapt to new tasks, they don't account for data modalities, they interact with losses, architectures and optimization in ways not yet fully understood. We conclude that new advances in the field are hinging on finding ways to incorporate data, tasks and learning into our definitions of smoothness.