Incremental Sequence Classification with Temporal Consistency

We address the problem of incremental sequence classification, where predictions are updated as new elements in the sequence are revealed. Drawing on temporal-difference learning from reinforcement learning, we identify a temporal-consistency condition that successive predictions should satisfy. We leverage this condition to develop a novel loss function for training incremental sequence classifiers. Through a concrete example, we demonstrate that optimizing this loss can offer substantial gains in data efficiency. We apply our method to text classification tasks and show that it improves predictive accuracy over competing approaches on several benchmark datasets. We further evaluate our approach on the task of verifying large language model generations for correctness in grade-school math problems. Our results show that models trained with our method are better able to distinguish promising generations from unpromising ones after observing only a few tokens.

Finding Increasingly Large Extremal Graphs with AlphaZero and Tabu Search

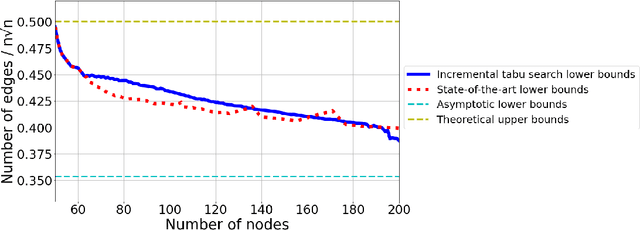
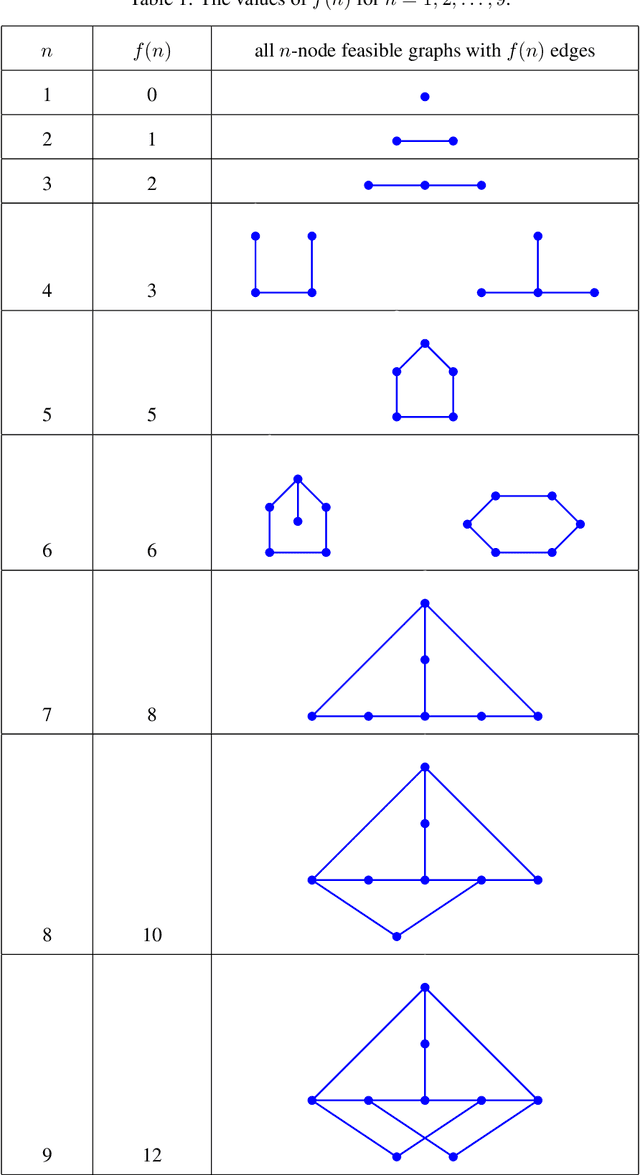
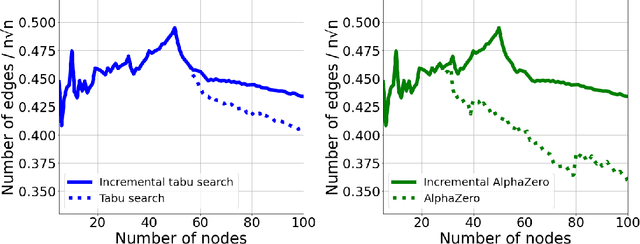
This work studies a central extremal graph theory problem inspired by a 1975 conjecture of Erd\H{o}s, which aims to find graphs with a given size (number of nodes) that maximize the number of edges without having 3- or 4-cycles. We formulate this problem as a sequential decision-making problem and compare AlphaZero, a neural network-guided tree search, with tabu search, a heuristic local search method. Using either method, by introducing a curriculum -- jump-starting the search for larger graphs using good graphs found at smaller sizes -- we improve the state-of-the-art lower bounds for several sizes. We also propose a flexible graph-generation environment and a permutation-invariant network architecture for learning to search in the space of graphs.

When Does Re-initialization Work?

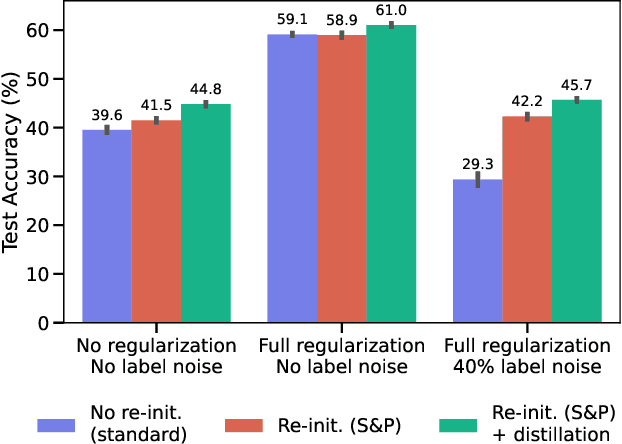
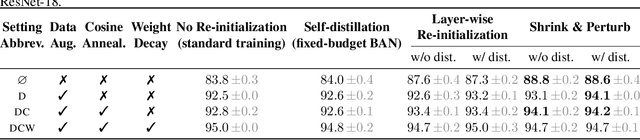
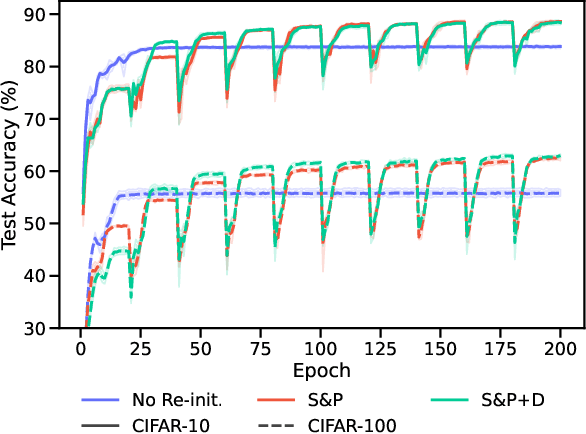
Re-initializing a neural network during training has been observed to improve generalization in recent works. Yet it is neither widely adopted in deep learning practice nor is it often used in state-of-the-art training protocols. This raises the question of when re-initialization works, and whether it should be used together with regularization techniques such as data augmentation, weight decay and learning rate schedules. In this work, we conduct an extensive empirical comparison of standard training with a selection of re-initialization methods to answer this question, training over 15,000 models on a variety of image classification benchmarks. We first establish that such methods are consistently beneficial for generalization in the absence of any other regularization. However, when deployed alongside other carefully tuned regularization techniques, re-initialization methods offer little to no added benefit for generalization, although optimal generalization performance becomes less sensitive to the choice of learning rate and weight decay hyperparameters. To investigate the impact of re-initialization methods on noisy data, we also consider learning under label noise. Surprisingly, in this case, re-initialization significantly improves upon standard training, even in the presence of other carefully tuned regularization techniques.

A study on the plasticity of neural networks

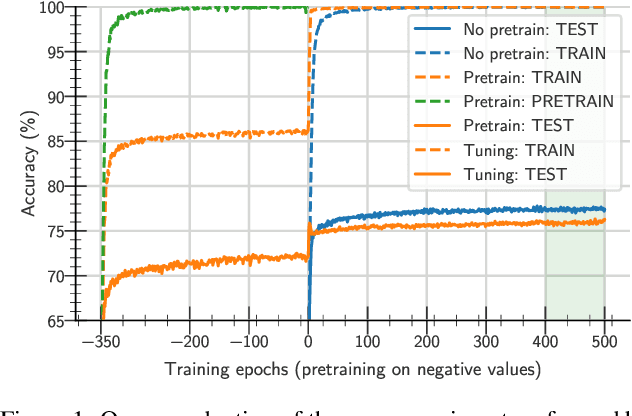
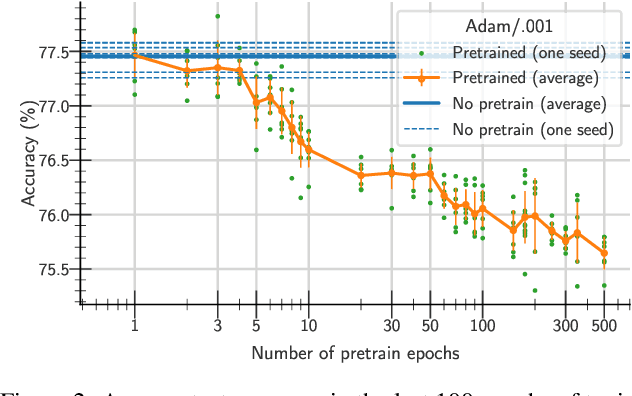
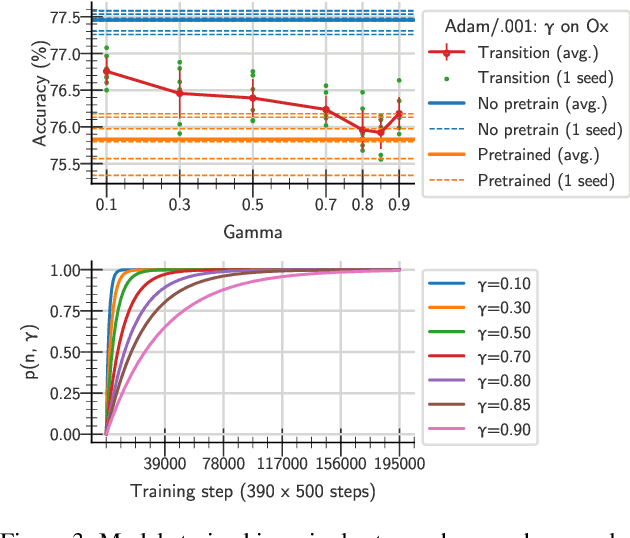
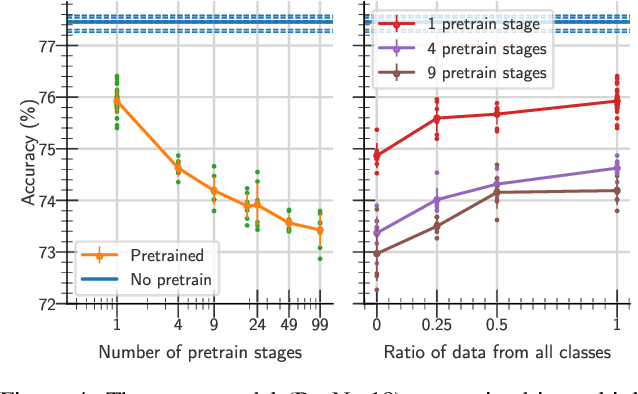
One aim shared by multiple settings, such as continual learning or transfer learning, is to leverage previously acquired knowledge to converge faster on the current task. Usually this is done through fine-tuning, where an implicit assumption is that the network maintains its plasticity, meaning that the performance it can reach on any given task is not affected negatively by previously seen tasks. It has been observed recently that a pretrained model on data from the same distribution as the one it is fine-tuned on might not reach the same generalisation as a freshly initialised one. We build and extend this observation, providing a hypothesis for the mechanics behind it. We discuss the implication of losing plasticity for continual learning which heavily relies on optimising pretrained models.

Spectral Normalisation for Deep Reinforcement Learning: an Optimisation Perspective

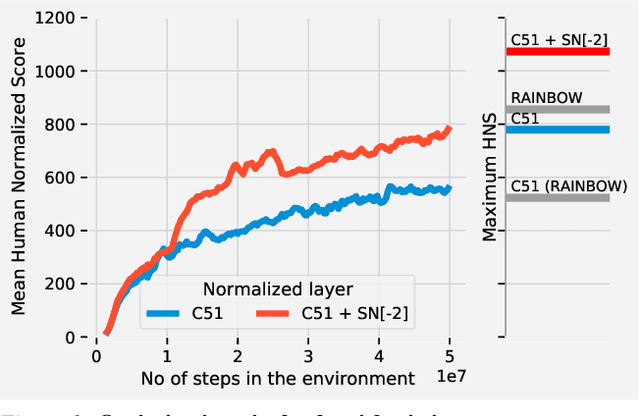
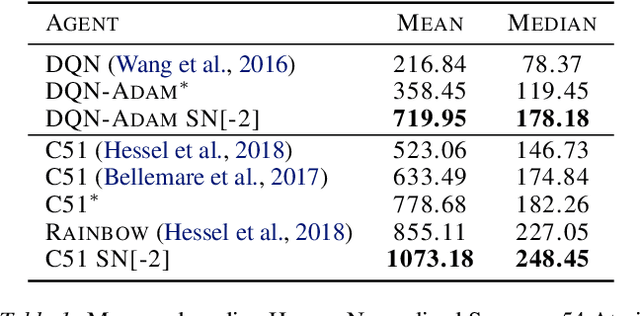
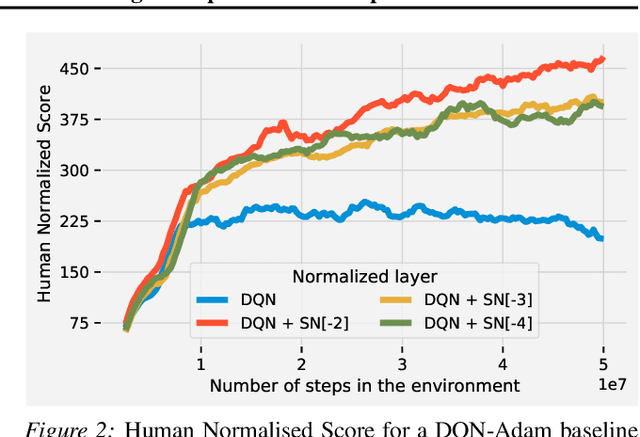
Most of the recent deep reinforcement learning advances take an RL-centric perspective and focus on refinements of the training objective. We diverge from this view and show we can recover the performance of these developments not by changing the objective, but by regularising the value-function estimator. Constraining the Lipschitz constant of a single layer using spectral normalisation is sufficient to elevate the performance of a Categorical-DQN agent to that of a more elaborated \rainbow{} agent on the challenging Atari domain. We conduct ablation studies to disentangle the various effects normalisation has on the learning dynamics and show that is sufficient to modulate the parameter updates to recover most of the performance of spectral normalisation. These findings hint towards the need to also focus on the neural component and its learning dynamics to tackle the peculiarities of Deep Reinforcement Learning.