Hyunjik Kim
MANZANO: A Simple and Scalable Unified Multimodal Model with a Hybrid Vision Tokenizer
Sep 19, 2025
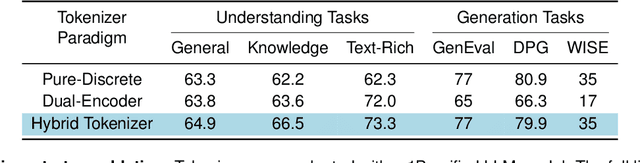
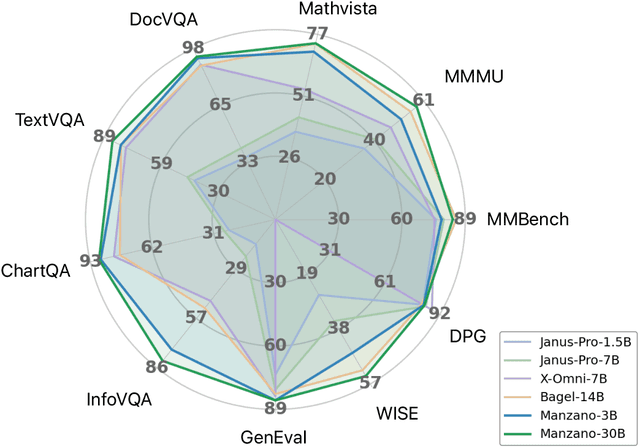
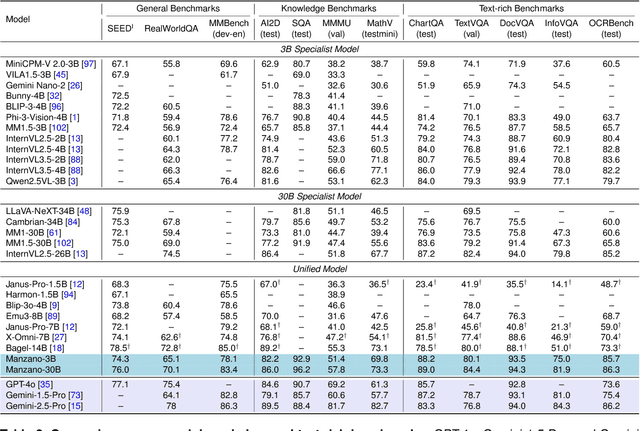
Abstract:Unified multimodal Large Language Models (LLMs) that can both understand and generate visual content hold immense potential. However, existing open-source models often suffer from a performance trade-off between these capabilities. We present Manzano, a simple and scalable unified framework that substantially reduces this tension by coupling a hybrid image tokenizer with a well-curated training recipe. A single shared vision encoder feeds two lightweight adapters that produce continuous embeddings for image-to-text understanding and discrete tokens for text-to-image generation within a common semantic space. A unified autoregressive LLM predicts high-level semantics in the form of text and image tokens, with an auxiliary diffusion decoder subsequently translating the image tokens into pixels. The architecture, together with a unified training recipe over understanding and generation data, enables scalable joint learning of both capabilities. Manzano achieves state-of-the-art results among unified models, and is competitive with specialist models, particularly on text-rich evaluation. Our studies show minimal task conflicts and consistent gains from scaling model size, validating our design choice of a hybrid tokenizer.
Good, Cheap, and Fast: Overfitted Image Compression with Wasserstein Distortion
Nov 30, 2024Abstract:Inspired by the success of generative image models, recent work on learned image compression increasingly focuses on better probabilistic models of the natural image distribution, leading to excellent image quality. This, however, comes at the expense of a computational complexity that is several orders of magnitude higher than today's commercial codecs, and thus prohibitive for most practical applications. With this paper, we demonstrate that by focusing on modeling visual perception rather than the data distribution, we can achieve a very good trade-off between visual quality and bit rate similar to "generative" compression models such as HiFiC, while requiring less than 1% of the multiply-accumulate operations (MACs) for decompression. We do this by optimizing C3, an overfitted image codec, for Wasserstein Distortion (WD), and evaluating the image reconstructions with a human rater study. The study also reveals that WD outperforms other perceptual quality metrics such as LPIPS, DISTS, and MS-SSIM, both as an optimization objective and as a predictor of human ratings, achieving over 94% Pearson correlation with Elo scores.
Neural Compression of Atmospheric States
Jul 16, 2024



Abstract:Atmospheric states derived from reanalysis comprise a substantial portion of weather and climate simulation outputs. Many stakeholders -- such as researchers, policy makers, and insurers -- use this data to better understand the earth system and guide policy decisions. Atmospheric states have also received increased interest as machine learning approaches to weather prediction have shown promising results. A key issue for all audiences is that dense time series of these high-dimensional states comprise an enormous amount of data, precluding all but the most well resourced groups from accessing and using historical data and future projections. To address this problem, we propose a method for compressing atmospheric states using methods from the neural network literature, adapting spherical data to processing by conventional neural architectures through the use of the area-preserving HEALPix projection. We investigate two model classes for building neural compressors: the hyperprior model from the neural image compression literature and recent vector-quantised models. We show that both families of models satisfy the desiderata of small average error, a small number of high-error reconstructed pixels, faithful reproduction of extreme events such as hurricanes and heatwaves, preservation of the spectral power distribution across spatial scales. We demonstrate compression ratios in excess of 1000x, with compression and decompression at a rate of approximately one second per global atmospheric state.
C3: High-performance and low-complexity neural compression from a single image or video
Dec 05, 2023Abstract:Most neural compression models are trained on large datasets of images or videos in order to generalize to unseen data. Such generalization typically requires large and expressive architectures with a high decoding complexity. Here we introduce C3, a neural compression method with strong rate-distortion (RD) performance that instead overfits a small model to each image or video separately. The resulting decoding complexity of C3 can be an order of magnitude lower than neural baselines with similar RD performance. C3 builds on COOL-CHIC (Ladune et al.) and makes several simple and effective improvements for images. We further develop new methodology to apply C3 to videos. On the CLIC2020 image benchmark, we match the RD performance of VTM, the reference implementation of the H.266 codec, with less than 3k MACs/pixel for decoding. On the UVG video benchmark, we match the RD performance of the Video Compression Transformer (Mentzer et al.), a well-established neural video codec, with less than 5k MACs/pixel for decoding.
Finding Increasingly Large Extremal Graphs with AlphaZero and Tabu Search
Nov 06, 2023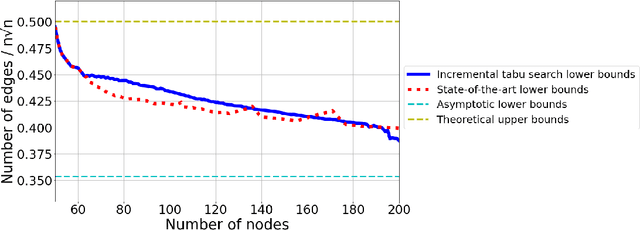
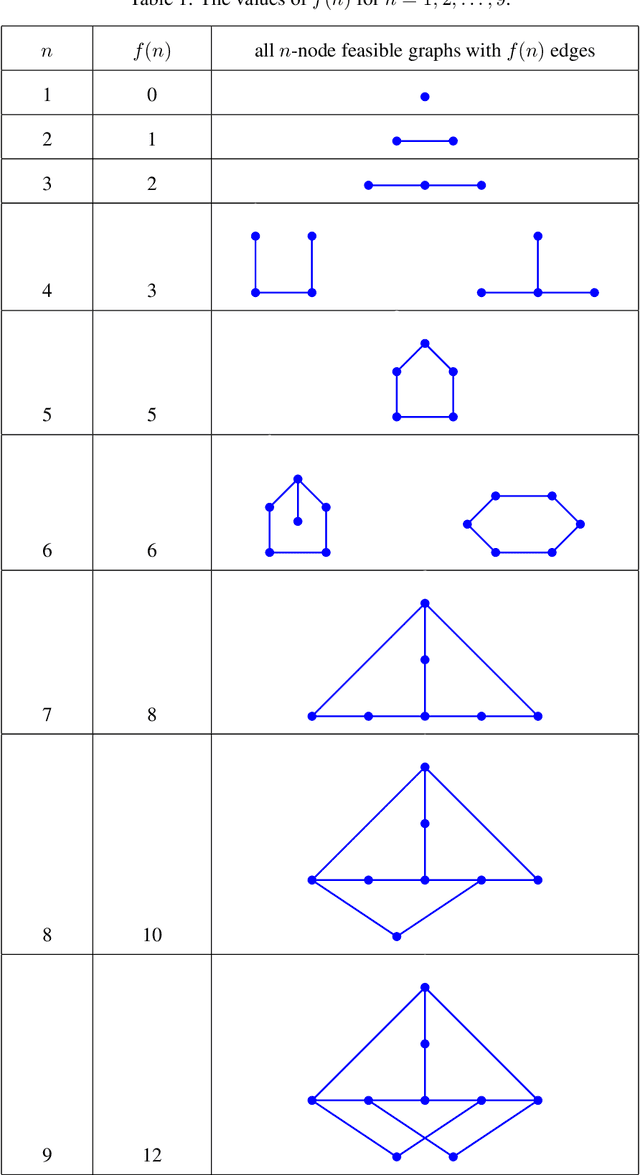
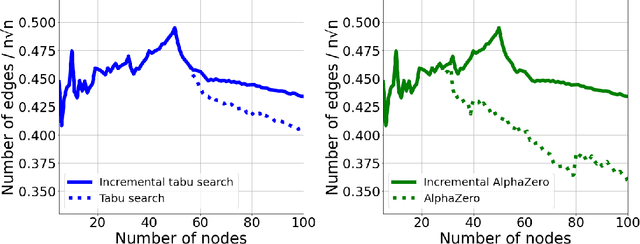

Abstract:This work studies a central extremal graph theory problem inspired by a 1975 conjecture of Erd\H{o}s, which aims to find graphs with a given size (number of nodes) that maximize the number of edges without having 3- or 4-cycles. We formulate this problem as a sequential decision-making problem and compare AlphaZero, a neural network-guided tree search, with tabu search, a heuristic local search method. Using either method, by introducing a curriculum -- jump-starting the search for larger graphs using good graphs found at smaller sizes -- we improve the state-of-the-art lower bounds for several sizes. We also propose a flexible graph-generation environment and a permutation-invariant network architecture for learning to search in the space of graphs.
Spatial Functa: Scaling Functa to ImageNet Classification and Generation
Feb 09, 2023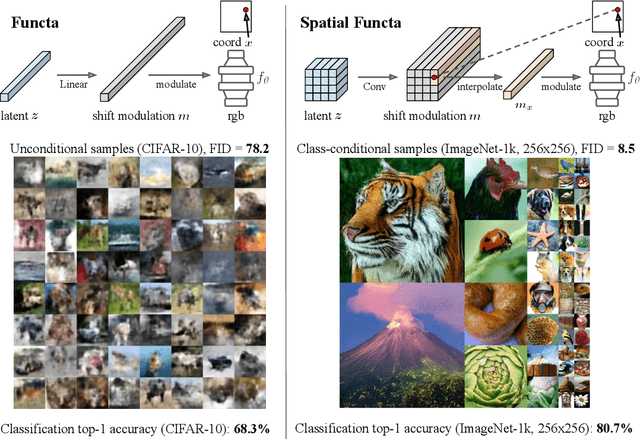
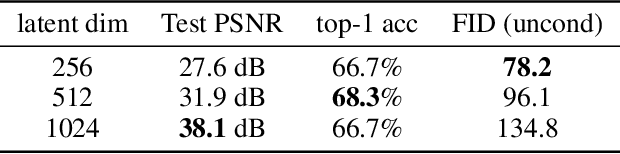


Abstract:Neural fields, also known as implicit neural representations, have emerged as a powerful means to represent complex signals of various modalities. Based on this Dupont et al. (2022) introduce a framework that views neural fields as data, termed *functa*, and proposes to do deep learning directly on this dataset of neural fields. In this work, we show that the proposed framework faces limitations when scaling up to even moderately complex datasets such as CIFAR-10. We then propose *spatial functa*, which overcome these limitations by using spatially arranged latent representations of neural fields, thereby allowing us to scale up the approach to ImageNet-1k at 256x256 resolution. We demonstrate competitive performance to Vision Transformers (Steiner et al., 2022) on classification and Latent Diffusion (Rombach et al., 2022) on image generation respectively.
When Does Re-initialization Work?
Jun 20, 2022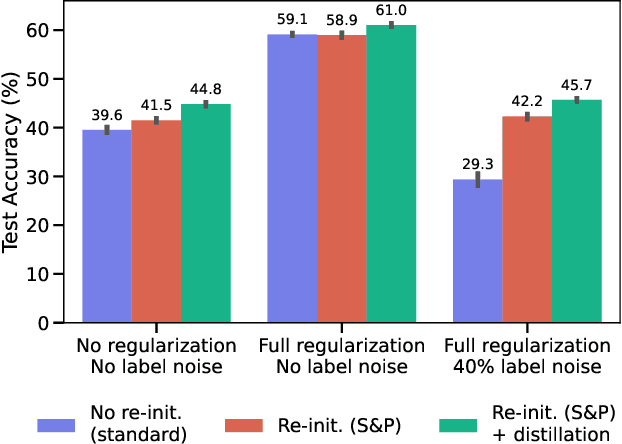
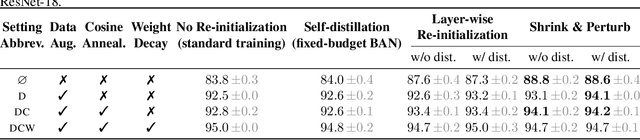
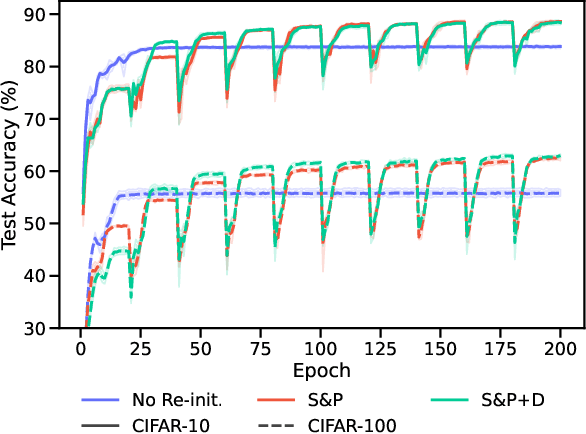

Abstract:Re-initializing a neural network during training has been observed to improve generalization in recent works. Yet it is neither widely adopted in deep learning practice nor is it often used in state-of-the-art training protocols. This raises the question of when re-initialization works, and whether it should be used together with regularization techniques such as data augmentation, weight decay and learning rate schedules. In this work, we conduct an extensive empirical comparison of standard training with a selection of re-initialization methods to answer this question, training over 15,000 models on a variety of image classification benchmarks. We first establish that such methods are consistently beneficial for generalization in the absence of any other regularization. However, when deployed alongside other carefully tuned regularization techniques, re-initialization methods offer little to no added benefit for generalization, although optimal generalization performance becomes less sensitive to the choice of learning rate and weight decay hyperparameters. To investigate the impact of re-initialization methods on noisy data, we also consider learning under label noise. Surprisingly, in this case, re-initialization significantly improves upon standard training, even in the presence of other carefully tuned regularization techniques.
Pre-training via Denoising for Molecular Property Prediction
May 31, 2022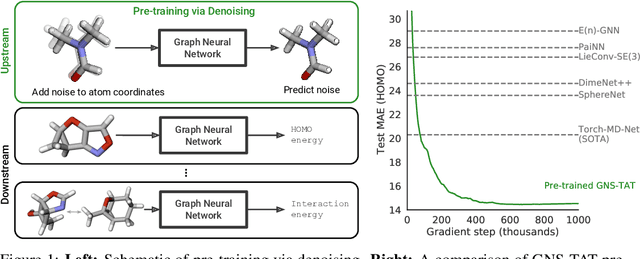
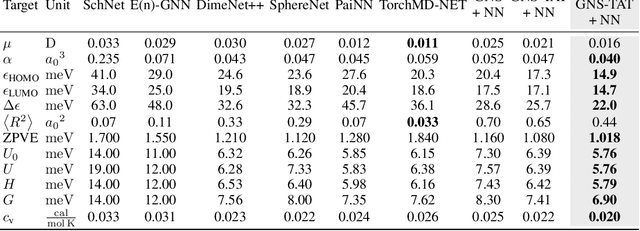
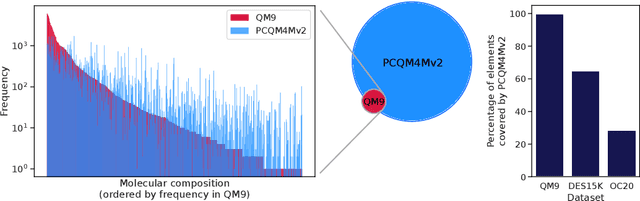
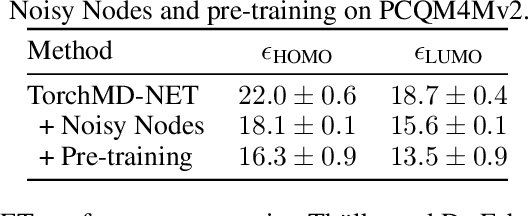
Abstract:Many important problems involving molecular property prediction from 3D structures have limited data, posing a generalization challenge for neural networks. In this paper, we describe a pre-training technique that utilizes large datasets of 3D molecular structures at equilibrium to learn meaningful representations for downstream tasks. Inspired by recent advances in noise regularization, our pre-training objective is based on denoising. Relying on the well-known link between denoising autoencoders and score-matching, we also show that the objective corresponds to learning a molecular force field -- arising from approximating the physical state distribution with a mixture of Gaussians -- directly from equilibrium structures. Our experiments demonstrate that using this pre-training objective significantly improves performance on multiple benchmarks, achieving a new state-of-the-art on the majority of targets in the widely used QM9 dataset. Our analysis then provides practical insights into the effects of different factors -- dataset sizes, model size and architecture, and the choice of upstream and downstream datasets -- on pre-training.
Learning Instance-Specific Data Augmentations
May 31, 2022
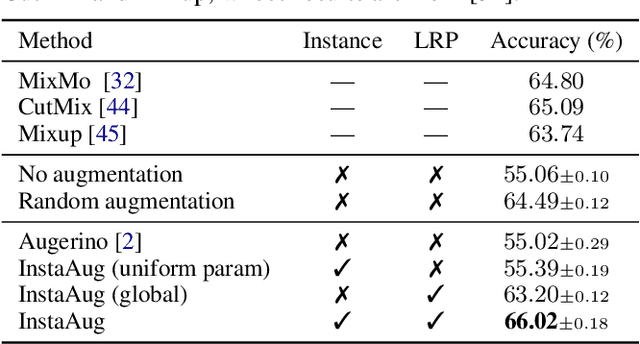
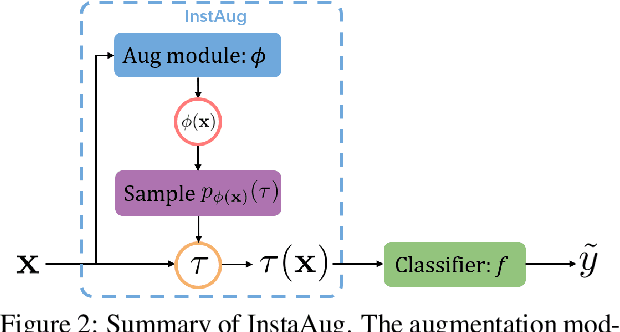
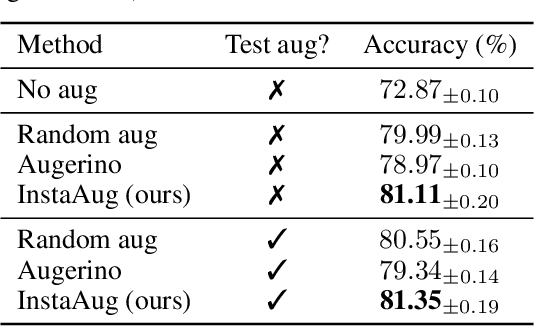
Abstract:Existing data augmentation methods typically assume independence between transformations and inputs: they use the same transformation distribution for all input instances. We explain why this can be problematic and propose InstaAug, a method for automatically learning input-specific augmentations from data. This is achieved by introducing an augmentation module that maps an input to a distribution over transformations. This is simultaneously trained alongside the base model in a fully end-to-end manner using only the training data. We empirically demonstrate that InstaAug learns meaningful augmentations for a wide range of transformation classes, which in turn provides better performance on supervised and self-supervised tasks compared with augmentations that assume input--transformation independence.
From data to functa: Your data point is a function and you should treat it like one
Jan 28, 2022



Abstract:It is common practice in deep learning to represent a measurement of the world on a discrete grid, e.g. a 2D grid of pixels. However, the underlying signal represented by these measurements is often continuous, e.g. the scene depicted in an image. A powerful continuous alternative is then to represent these measurements using an implicit neural representation, a neural function trained to output the appropriate measurement value for any input spatial location. In this paper, we take this idea to its next level: what would it take to perform deep learning on these functions instead, treating them as data? In this context we refer to the data as functa, and propose a framework for deep learning on functa. This view presents a number of challenges around efficient conversion from data to functa, compact representation of functa, and effectively solving downstream tasks on functa. We outline a recipe to overcome these challenges and apply it to a wide range of data modalities including images, 3D shapes, neural radiance fields (NeRF) and data on manifolds. We demonstrate that this approach has various compelling properties across data modalities, in particular on the canonical tasks of generative modeling, data imputation, novel view synthesis and classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge