Rethinking Aleatoric and Epistemic Uncertainty

The ideas of aleatoric and epistemic uncertainty are widely used to reason about the probabilistic predictions of machine-learning models. We identify incoherence in existing discussions of these ideas and suggest this stems from the aleatoric-epistemic view being insufficiently expressive to capture all of the distinct quantities that researchers are interested in. To explain and address this we derive a simple delineation of different model-based uncertainties and the data-generating processes associated with training and evaluation. Using this in place of the aleatoric-epistemic view could produce clearer discourse as the field moves forward.

Highly Accurate Real-space Electron Densities with Neural Networks

Variational ab-initio methods in quantum chemistry stand out among other methods in providing direct access to the wave function. This allows in principle straightforward extraction of any other observable of interest, besides the energy, but in practice this extraction is often technically difficult and computationally impractical. Here, we consider the electron density as a central observable in quantum chemistry and introduce a novel method to obtain accurate densities from real-space many-electron wave functions by representing the density with a neural network that captures known asymptotic properties and is trained from the wave function by score matching and noise-contrastive estimation. We use variational quantum Monte Carlo with deep-learning ans\"atze (deep QMC) to obtain highly accurate wave functions free of basis set errors, and from them, using our novel method, correspondingly accurate electron densities, which we demonstrate by calculating dipole moments, nuclear forces, contact densities, and other density-based properties.

Amortized Active Causal Induction with Deep Reinforcement Learning

We present Causal Amortized Active Structure Learning (CAASL), an active intervention design policy that can select interventions that are adaptive, real-time and that does not require access to the likelihood. This policy, an amortized network based on the transformer, is trained with reinforcement learning on a simulator of the design environment, and a reward function that measures how close the true causal graph is to a causal graph posterior inferred from the gathered data. On synthetic data and a single-cell gene expression simulator, we demonstrate empirically that the data acquired through our policy results in a better estimate of the underlying causal graph than alternative strategies. Our design policy successfully achieves amortized intervention design on the distribution of the training environment while also generalizing well to distribution shifts in test-time design environments. Further, our policy also demonstrates excellent zero-shot generalization to design environments with dimensionality higher than that during training, and to intervention types that it has not been trained on.

Making Better Use of Unlabelled Data in Bayesian Active Learning

Fully supervised models are predominant in Bayesian active learning. We argue that their neglect of the information present in unlabelled data harms not just predictive performance but also decisions about what data to acquire. Our proposed solution is a simple framework for semi-supervised Bayesian active learning. We find it produces better-performing models than either conventional Bayesian active learning or semi-supervised learning with randomly acquired data. It is also easier to scale up than the conventional approach. As well as supporting a shift towards semi-supervised models, our findings highlight the importance of studying models and acquisition methods in conjunction.

Prediction-Oriented Bayesian Active Learning

Information-theoretic approaches to active learning have traditionally focused on maximising the information gathered about the model parameters, most commonly by optimising the BALD score. We highlight that this can be suboptimal from the perspective of predictive performance. For example, BALD lacks a notion of an input distribution and so is prone to prioritise data of limited relevance. To address this we propose the expected predictive information gain (EPIG), an acquisition function that measures information gain in the space of predictions rather than parameters. We find that using EPIG leads to stronger predictive performance compared with BALD across a range of datasets and models, and thus provides an appealing drop-in replacement.

Modern Bayesian Experimental Design

Bayesian experimental design (BED) provides a powerful and general framework for optimizing the design of experiments. However, its deployment often poses substantial computational challenges that can undermine its practical use. In this review, we outline how recent advances have transformed our ability to overcome these challenges and thus utilize BED effectively, before discussing some key areas for future development in the field.

CO-BED: Information-Theoretic Contextual Optimization via Bayesian Experimental Design

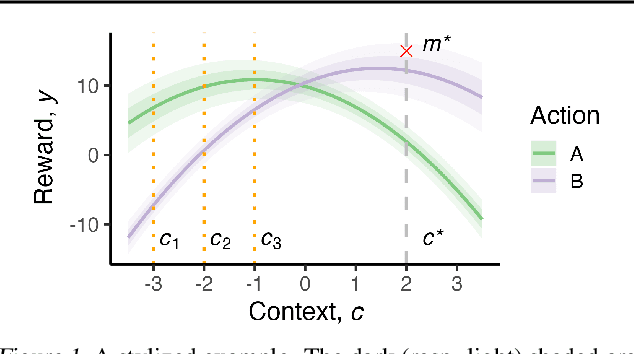
We formalize the problem of contextual optimization through the lens of Bayesian experimental design and propose CO-BED -- a general, model-agnostic framework for designing contextual experiments using information-theoretic principles. After formulating a suitable information-based objective, we employ black-box variational methods to simultaneously estimate it and optimize the designs in a single stochastic gradient scheme. We further introduce a relaxation scheme to allow discrete actions to be accommodated. As a result, CO-BED provides a general and automated solution to a wide range of contextual optimization problems. We illustrate its effectiveness in a number of experiments, where CO-BED demonstrates competitive performance even when compared to bespoke, model-specific alternatives.

Differentiable Multi-Target Causal Bayesian Experimental Design

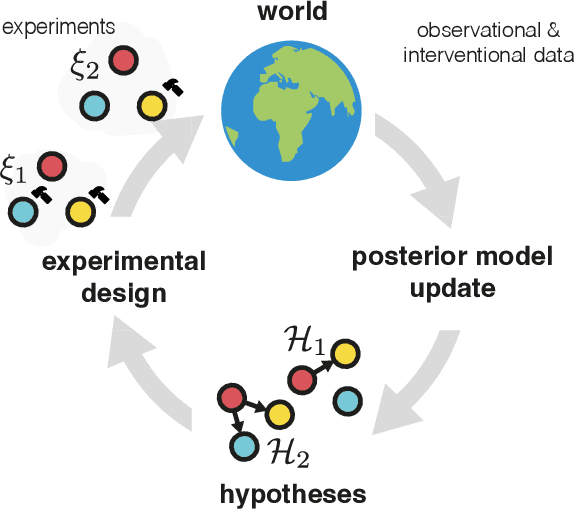
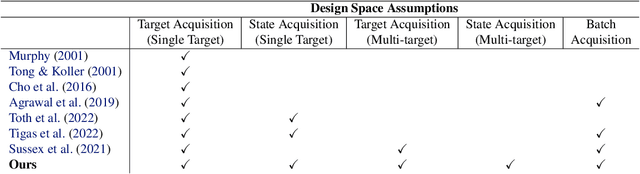
We introduce a gradient-based approach for the problem of Bayesian optimal experimental design to learn causal models in a batch setting -- a critical component for causal discovery from finite data where interventions can be costly or risky. Existing methods rely on greedy approximations to construct a batch of experiments while using black-box methods to optimize over a single target-state pair to intervene with. In this work, we completely dispose of the black-box optimization techniques and greedy heuristics and instead propose a conceptually simple end-to-end gradient-based optimization procedure to acquire a set of optimal intervention target-state pairs. Such a procedure enables parameterization of the design space to efficiently optimize over a batch of multi-target-state interventions, a setting which has hitherto not been explored due to its complexity. We demonstrate that our proposed method outperforms baselines and existing acquisition strategies in both single-target and multi-target settings across a number of synthetic datasets.

Efficient Real-world Testing of Causal Decision Making via Bayesian Experimental Design for Contextual Optimisation

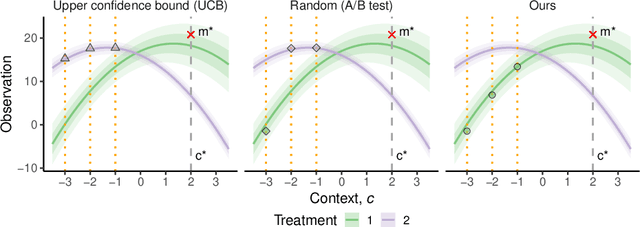
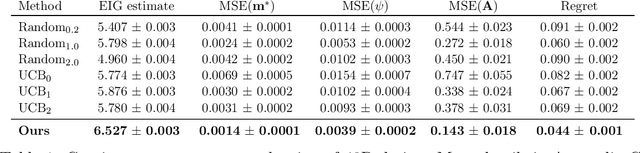
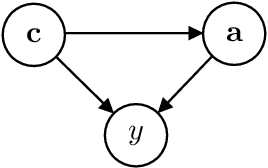
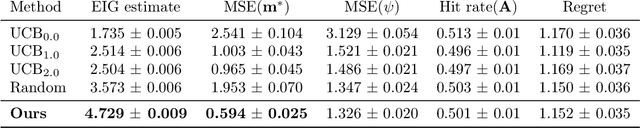
The real-world testing of decisions made using causal machine learning models is an essential prerequisite for their successful application. We focus on evaluating and improving contextual treatment assignment decisions: these are personalised treatments applied to e.g. customers, each with their own contextual information, with the aim of maximising a reward. In this paper we introduce a model-agnostic framework for gathering data to evaluate and improve contextual decision making through Bayesian Experimental Design. Specifically, our method is used for the data-efficient evaluation of the regret of past treatment assignments. Unlike approaches such as A/B testing, our method avoids assigning treatments that are known to be highly sub-optimal, whilst engaging in some exploration to gather pertinent information. We achieve this by introducing an information-based design objective, which we optimise end-to-end. Our method applies to discrete and continuous treatments. Comparing our information-theoretic approach to baselines in several simulation studies demonstrates the superior performance of our proposed approach.

Learning Instance-Specific Data Augmentations

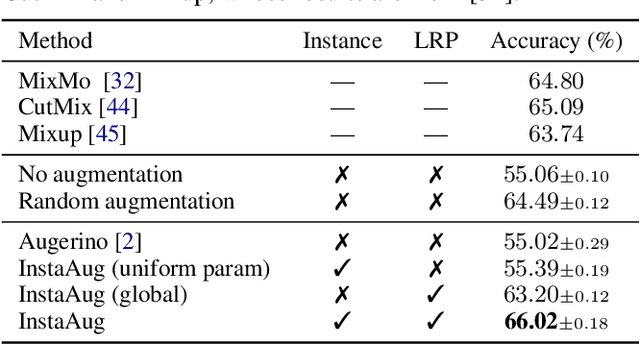
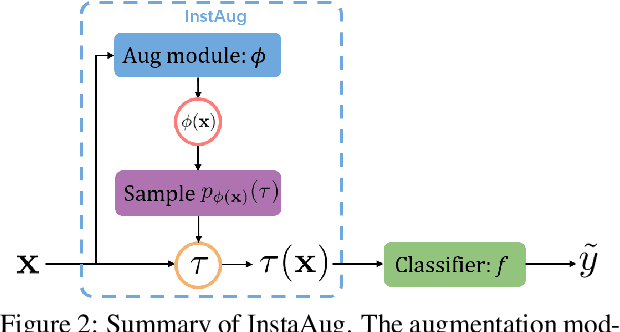
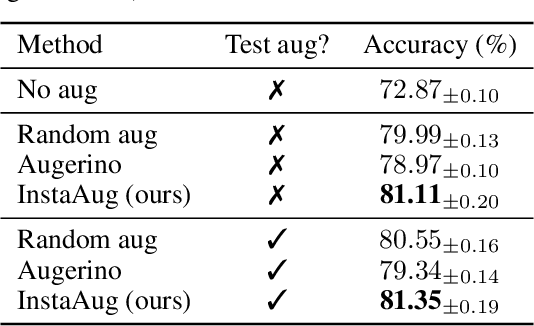
Existing data augmentation methods typically assume independence between transformations and inputs: they use the same transformation distribution for all input instances. We explain why this can be problematic and propose InstaAug, a method for automatically learning input-specific augmentations from data. This is achieved by introducing an augmentation module that maps an input to a distribution over transformations. This is simultaneously trained alongside the base model in a fully end-to-end manner using only the training data. We empirically demonstrate that InstaAug learns meaningful augmentations for a wide range of transformation classes, which in turn provides better performance on supervised and self-supervised tasks compared with augmentations that assume input--transformation independence.