FiP: a Fixed-Point Approach for Causal Generative Modeling

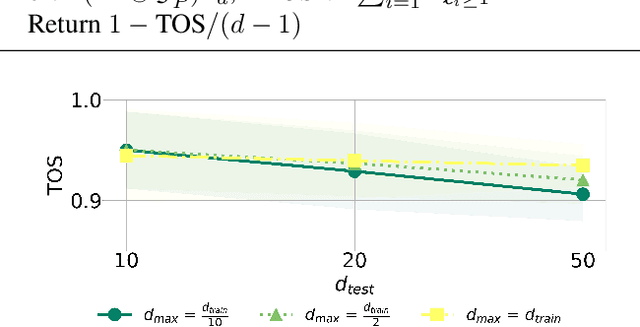
Modeling true world data-generating processes lies at the heart of empirical science. Structural Causal Models (SCMs) and their associated Directed Acyclic Graphs (DAGs) provide an increasingly popular answer to such problems by defining the causal generative process that transforms random noise into observations. However, learning them from observational data poses an ill-posed and NP-hard inverse problem in general. In this work, we propose a new and equivalent formalism that does not require DAGs to describe them, viewed as fixed-point problems on the causally ordered variables, and we show three important cases where they can be uniquely recovered given the topological ordering (TO). To the best of our knowledge, we obtain the weakest conditions for their recovery when TO is known. Based on this, we design a two-stage causal generative model that first infers the causal order from observations in a zero-shot manner, thus by-passing the search, and then learns the generative fixed-point SCM on the ordered variables. To infer TOs from observations, we propose to amortize the learning of TOs on generated datasets by sequentially predicting the leaves of graphs seen during training. To learn fixed-point SCMs, we design a transformer-based architecture that exploits a new attention mechanism enabling the modeling of causal structures, and show that this parameterization is consistent with our formalism. Finally, we conduct an extensive evaluation of each method individually, and show that when combined, our model outperforms various baselines on generated out-of-distribution problems.

Neural Structure Learning with Stochastic Differential Equations

Discovering the underlying relationships among variables from temporal observations has been a longstanding challenge in numerous scientific disciplines, including biology, finance, and climate science. The dynamics of such systems are often best described using continuous-time stochastic processes. Unfortunately, most existing structure learning approaches assume that the underlying process evolves in discrete-time and/or observations occur at regular time intervals. These mismatched assumptions can often lead to incorrect learned structures and models. In this work, we introduce a novel structure learning method, SCOTCH, which combines neural stochastic differential equations (SDE) with variational inference to infer a posterior distribution over possible structures. This continuous-time approach can naturally handle both learning from and predicting observations at arbitrary time points. Theoretically, we establish sufficient conditions for an SDE and SCOTCH to be structurally identifiable, and prove its consistency under infinite data limits. Empirically, we demonstrate that our approach leads to improved structure learning performance on both synthetic and real-world datasets compared to relevant baselines under regular and irregular sampling intervals.

Towards Causal Foundation Model: on Duality between Causal Inference and Attention

Foundation models have brought changes to the landscape of machine learning, demonstrating sparks of human-level intelligence across a diverse array of tasks. However, a gap persists in complex tasks such as causal inference, primarily due to challenges associated with intricate reasoning steps and high numerical precision requirements. In this work, we take a first step towards building causally-aware foundation models for complex tasks. We propose a novel, theoretically sound method called Causal Inference with Attention (CInA), which utilizes multiple unlabeled datasets to perform self-supervised causal learning, and subsequently enables zero-shot causal inference on unseen tasks with new data. This is based on our theoretical results that demonstrate the primal-dual connection between optimal covariate balancing and self-attention, facilitating zero-shot causal inference through the final layer of a trained transformer-type architecture. We demonstrate empirically that our approach CInA effectively generalizes to out-of-distribution datasets and various real-world datasets, matching or even surpassing traditional per-dataset causal inference methodologies.

BayesDAG: Gradient-Based Posterior Sampling for Causal Discovery

Bayesian causal discovery aims to infer the posterior distribution over causal models from observed data, quantifying epistemic uncertainty and benefiting downstream tasks. However, computational challenges arise due to joint inference over combinatorial space of Directed Acyclic Graphs (DAGs) and nonlinear functions. Despite recent progress towards efficient posterior inference over DAGs, existing methods are either limited to variational inference on node permutation matrices for linear causal models, leading to compromised inference accuracy, or continuous relaxation of adjacency matrices constrained by a DAG regularizer, which cannot ensure resulting graphs are DAGs. In this work, we introduce a scalable Bayesian causal discovery framework based on stochastic gradient Markov Chain Monte Carlo (SG-MCMC) that overcomes these limitations. Our approach directly samples DAGs from the posterior without requiring any DAG regularization, simultaneously draws function parameter samples and is applicable to both linear and nonlinear causal models. To enable our approach, we derive a novel equivalence to the permutation-based DAG learning, which opens up possibilities of using any relaxed gradient estimator defined over permutations. To our knowledge, this is the first framework applying gradient-based MCMC sampling for causal discovery. Empirical evaluations on synthetic and real-world datasets demonstrate our approach's effectiveness compared to state-of-the-art baselines.

Understanding Causality with Large Language Models: Feasibility and Opportunities

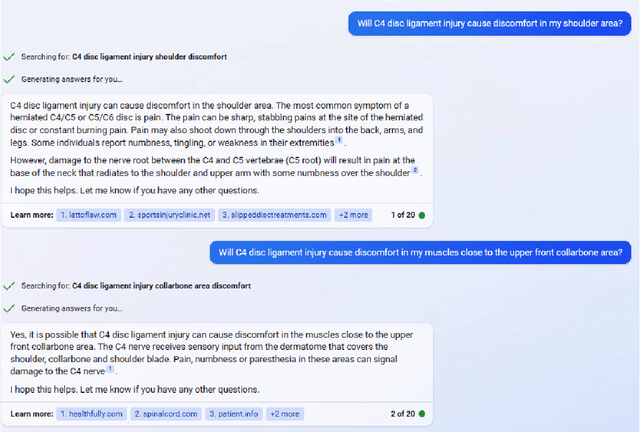
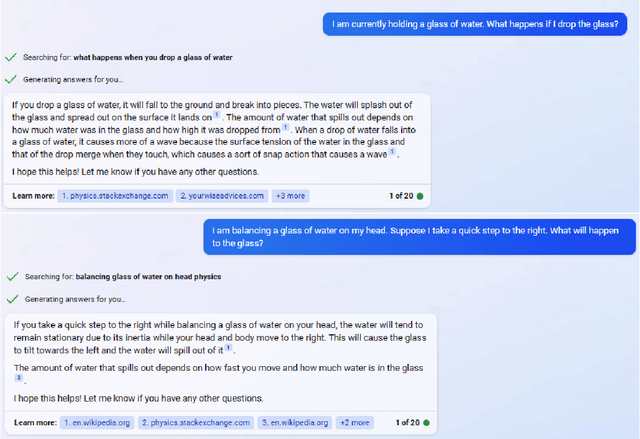
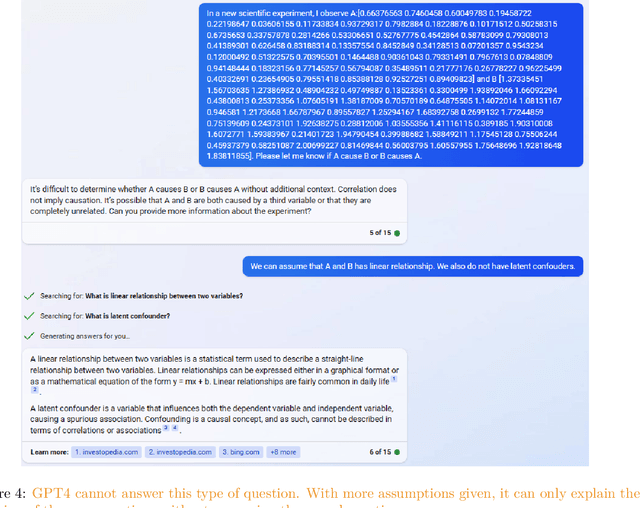
We assess the ability of large language models (LLMs) to answer causal questions by analyzing their strengths and weaknesses against three types of causal question. We believe that current LLMs can answer causal questions with existing causal knowledge as combined domain experts. However, they are not yet able to provide satisfactory answers for discovering new knowledge or for high-stakes decision-making tasks with high precision. We discuss possible future directions and opportunities, such as enabling explicit and implicit causal modules as well as deep causal-aware LLMs. These will not only enable LLMs to answer many different types of causal questions for greater impact but also enable LLMs to be more trustworthy and efficient in general.

Causal Reasoning in the Presence of Latent Confounders via Neural ADMG Learning

Latent confounding has been a long-standing obstacle for causal reasoning from observational data. One popular approach is to model the data using acyclic directed mixed graphs (ADMGs), which describe ancestral relations between variables using directed and bidirected edges. However, existing methods using ADMGs are based on either linear functional assumptions or a discrete search that is complicated to use and lacks computational tractability for large datasets. In this work, we further extend the existing body of work and develop a novel gradient-based approach to learning an ADMG with non-linear functional relations from observational data. We first show that the presence of latent confounding is identifiable under the assumptions of bow-free ADMGs with non-linear additive noise models. With this insight, we propose a novel neural causal model based on autoregressive flows for ADMG learning. This not only enables us to determine complex causal structural relationships behind the data in the presence of latent confounding, but also estimate their functional relationships (hence treatment effects) simultaneously. We further validate our approach via experiments on both synthetic and real-world datasets, and demonstrate the competitive performance against relevant baselines.

CO-BED: Information-Theoretic Contextual Optimization via Bayesian Experimental Design

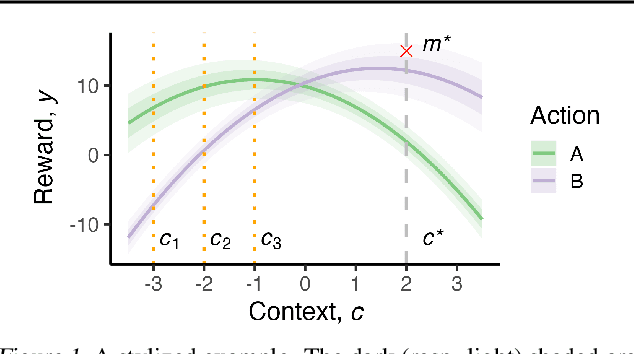
We formalize the problem of contextual optimization through the lens of Bayesian experimental design and propose CO-BED -- a general, model-agnostic framework for designing contextual experiments using information-theoretic principles. After formulating a suitable information-based objective, we employ black-box variational methods to simultaneously estimate it and optimize the designs in a single stochastic gradient scheme. We further introduce a relaxation scheme to allow discrete actions to be accommodated. As a result, CO-BED provides a general and automated solution to a wide range of contextual optimization problems. We illustrate its effectiveness in a number of experiments, where CO-BED demonstrates competitive performance even when compared to bespoke, model-specific alternatives.

Rhino: Deep Causal Temporal Relationship Learning With History-dependent Noise

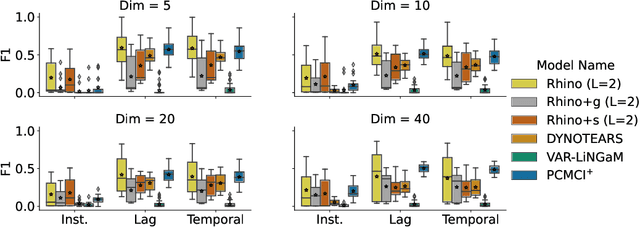
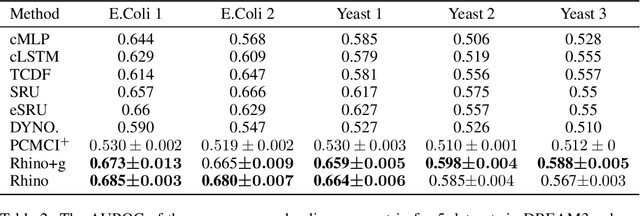
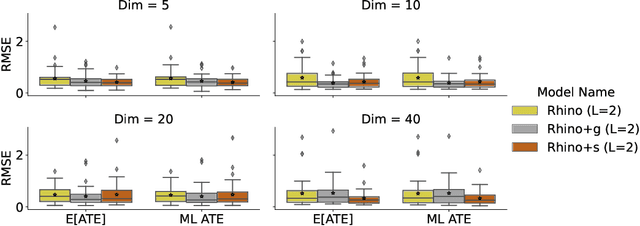
Discovering causal relationships between different variables from time series data has been a long-standing challenge for many domains such as climate science, finance, and healthcare. Given the complexity of real-world relationships and the nature of observations in discrete time, causal discovery methods need to consider non-linear relations between variables, instantaneous effects and history-dependent noise (the change of noise distribution due to past actions). However, previous works do not offer a solution addressing all these problems together. In this paper, we propose a novel causal relationship learning framework for time-series data, called Rhino, which combines vector auto-regression, deep learning and variational inference to model non-linear relationships with instantaneous effects while allowing the noise distribution to be modulated by historical observations. Theoretically, we prove the structural identifiability of Rhino. Our empirical results from extensive synthetic experiments and two real-world benchmarks demonstrate better discovery performance compared to relevant baselines, with ablation studies revealing its robustness under model misspecification.

NeurIPS Competition Instructions and Guide: Causal Insights for Learning Paths in Education

In this competition, participants will address two fundamental causal challenges in machine learning in the context of education using time-series data. The first is to identify the causal relationships between different constructs, where a construct is defined as the smallest element of learning. The second challenge is to predict the impact of learning one construct on the ability to answer questions on other constructs. Addressing these challenges will enable optimisation of students' knowledge acquisition, which can be deployed in a real edtech solution impacting millions of students. Participants will run these tasks in an idealised environment with synthetic data and a real-world scenario with evaluation data collected from a series of A/B tests.

Efficient Real-world Testing of Causal Decision Making via Bayesian Experimental Design for Contextual Optimisation

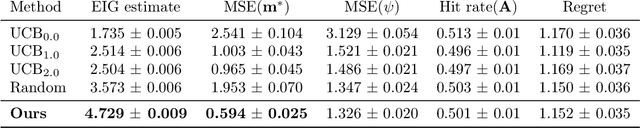
The real-world testing of decisions made using causal machine learning models is an essential prerequisite for their successful application. We focus on evaluating and improving contextual treatment assignment decisions: these are personalised treatments applied to e.g. customers, each with their own contextual information, with the aim of maximising a reward. In this paper we introduce a model-agnostic framework for gathering data to evaluate and improve contextual decision making through Bayesian Experimental Design. Specifically, our method is used for the data-efficient evaluation of the regret of past treatment assignments. Unlike approaches such as A/B testing, our method avoids assigning treatments that are known to be highly sub-optimal, whilst engaging in some exploration to gather pertinent information. We achieve this by introducing an information-based design objective, which we optimise end-to-end. Our method applies to discrete and continuous treatments. Comparing our information-theoretic approach to baselines in several simulation studies demonstrates the superior performance of our proposed approach.