In-Context In-Context Learning with Transformer Neural Processes

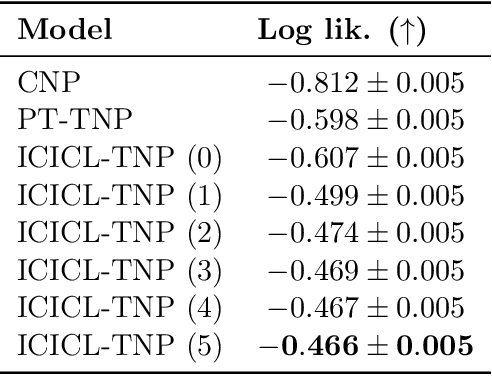
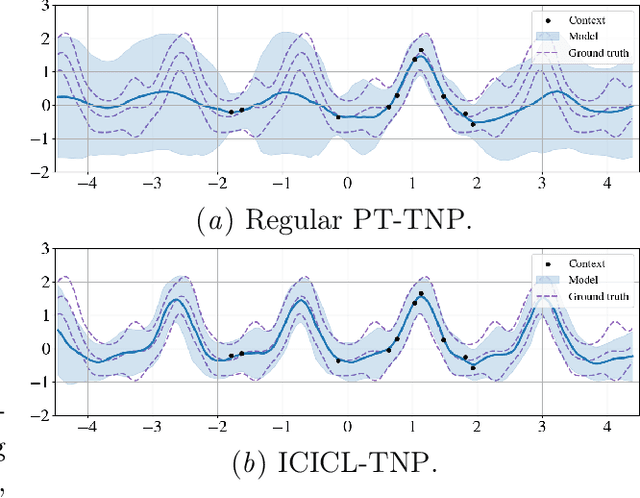
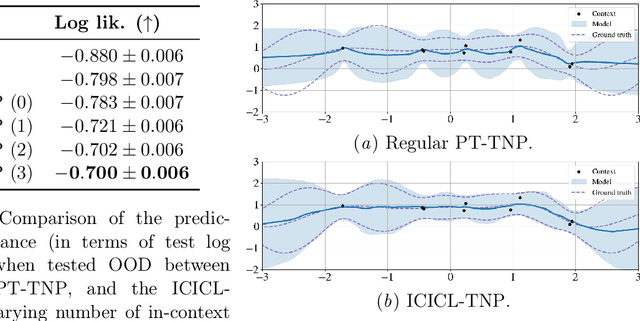
Neural processes (NPs) are a powerful family of meta-learning models that seek to approximate the posterior predictive map of the ground-truth stochastic process from which each dataset in a meta-dataset is sampled. There are many cases in which practitioners, besides having access to the dataset of interest, may also have access to other datasets that share similarities with it. In this case, integrating these datasets into the NP can improve predictions. We equip NPs with this functionality and describe this paradigm as in-context in-context learning. Standard NP architectures, such as the convolutional conditional NP (ConvCNP) or the family of transformer neural processes (TNPs), are not capable of in-context in-context learning, as they are only able to condition on a single dataset. We address this shortcoming by developing the in-context in-context learning pseudo-token TNP (ICICL-TNP). The ICICL-TNP builds on the family of PT-TNPs, which utilise pseudo-token-based transformer architectures to sidestep the quadratic computational complexity associated with regular transformer architectures. Importantly, the ICICL-TNP is capable of conditioning on both sets of datapoints and sets of datasets, enabling it to perform in-context in-context learning. We demonstrate the importance of in-context in-context learning and the effectiveness of the ICICL-TNP in a number of experiments.

Approximately Equivariant Neural Processes

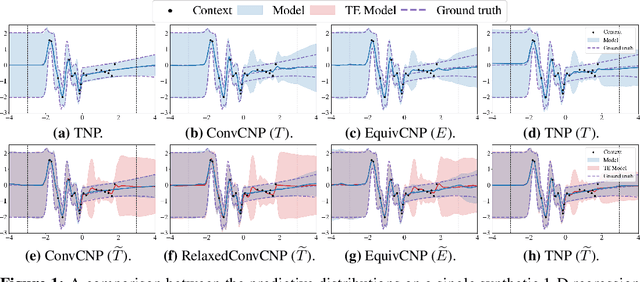
Equivariant deep learning architectures exploit symmetries in learning problems to improve the sample efficiency of neural-network-based models and their ability to generalise. However, when modelling real-world data, learning problems are often not exactly equivariant, but only approximately. For example, when estimating the global temperature field from weather station observations, local topographical features like mountains break translation equivariance. In these scenarios, it is desirable to construct architectures that can flexibly depart from exact equivariance in a data-driven way. In this paper, we develop a general approach to achieving this using existing equivariant architectures. Our approach is agnostic to both the choice of symmetry group and model architecture, making it widely applicable. We consider the use of approximately equivariant architectures in neural processes (NPs), a popular family of meta-learning models. We demonstrate the effectiveness of our approach on a number of synthetic and real-world regression experiments, demonstrating that approximately equivariant NP models can outperform both their non-equivariant and strictly equivariant counterparts.

Translation Equivariant Transformer Neural Processes

The effectiveness of neural processes (NPs) in modelling posterior prediction maps -- the mapping from data to posterior predictive distributions -- has significantly improved since their inception. This improvement can be attributed to two principal factors: (1) advancements in the architecture of permutation invariant set functions, which are intrinsic to all NPs; and (2) leveraging symmetries present in the true posterior predictive map, which are problem dependent. Transformers are a notable development in permutation invariant set functions, and their utility within NPs has been demonstrated through the family of models we refer to as TNPs. Despite significant interest in TNPs, little attention has been given to incorporating symmetries. Notably, the posterior prediction maps for data that are stationary -- a common assumption in spatio-temporal modelling -- exhibit translation equivariance. In this paper, we introduce of a new family of translation equivariant TNPs that incorporate translation equivariance. Through an extensive range of experiments on synthetic and real-world spatio-temporal data, we demonstrate the effectiveness of TE-TNPs relative to their non-translation-equivariant counterparts and other NP baselines.

Noise-Aware Differentially Private Regression via Meta-Learning

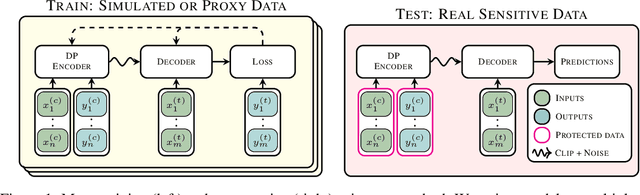
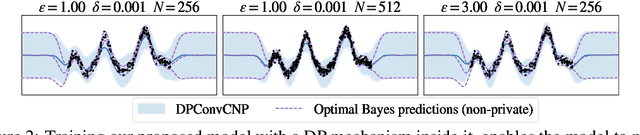
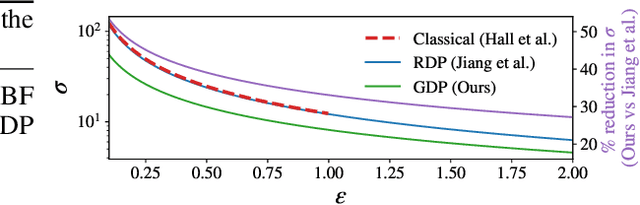
Many high-stakes applications require machine learning models that protect user privacy and provide well-calibrated, accurate predictions. While Differential Privacy (DP) is the gold standard for protecting user privacy, standard DP mechanisms typically significantly impair performance. One approach to mitigating this issue is pre-training models on simulated data before DP learning on the private data. In this work we go a step further, using simulated data to train a meta-learning model that combines the Convolutional Conditional Neural Process (ConvCNP) with an improved functional DP mechanism of Hall et al. [2013] yielding the DPConvCNP. DPConvCNP learns from simulated data how to map private data to a DP predictive model in one forward pass, and then provides accurate, well-calibrated predictions. We compare DPConvCNP with a DP Gaussian Process (GP) baseline with carefully tuned hyperparameters. The DPConvCNP outperforms the GP baseline, especially on non-Gaussian data, yet is much faster at test time and requires less tuning.

Amortised Inference in Neural Networks for Small-Scale Probabilistic Meta-Learning

The global inducing point variational approximation for BNNs is based on using a set of inducing inputs to construct a series of conditional distributions that accurately approximate the conditionals of the true posterior distribution. Our key insight is that these inducing inputs can be replaced by the actual data, such that the variational distribution consists of a set of approximate likelihoods for each datapoint. This structure lends itself to amortised inference, in which the parameters of each approximate likelihood are obtained by passing each datapoint through a meta-model known as the inference network. By training this inference network across related datasets, we can meta-learn Bayesian inference over task-specific BNNs.

Causal Reasoning in the Presence of Latent Confounders via Neural ADMG Learning

Latent confounding has been a long-standing obstacle for causal reasoning from observational data. One popular approach is to model the data using acyclic directed mixed graphs (ADMGs), which describe ancestral relations between variables using directed and bidirected edges. However, existing methods using ADMGs are based on either linear functional assumptions or a discrete search that is complicated to use and lacks computational tractability for large datasets. In this work, we further extend the existing body of work and develop a novel gradient-based approach to learning an ADMG with non-linear functional relations from observational data. We first show that the presence of latent confounding is identifiable under the assumptions of bow-free ADMGs with non-linear additive noise models. With this insight, we propose a novel neural causal model based on autoregressive flows for ADMG learning. This not only enables us to determine complex causal structural relationships behind the data in the presence of latent confounding, but also estimate their functional relationships (hence treatment effects) simultaneously. We further validate our approach via experiments on both synthetic and real-world datasets, and demonstrate the competitive performance against relevant baselines.

Differentially private partitioned variational inference

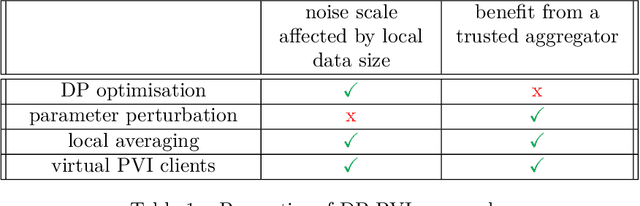
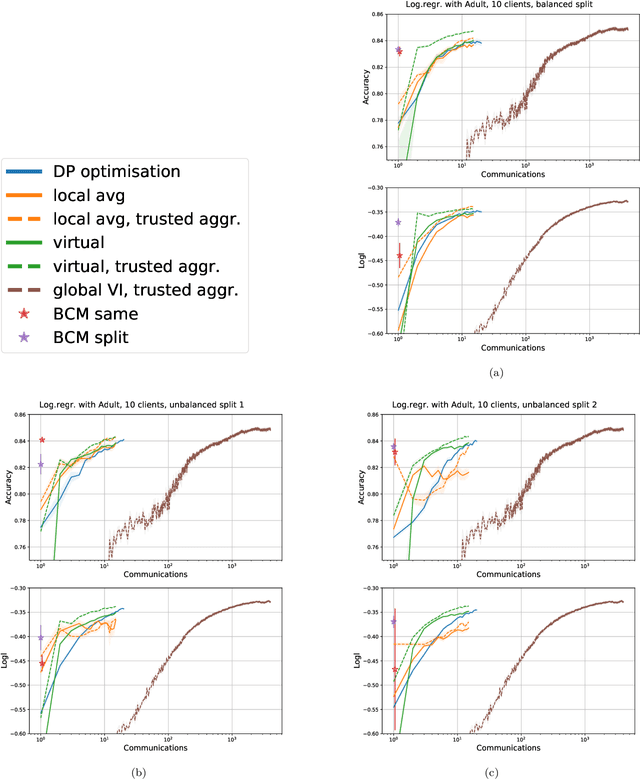
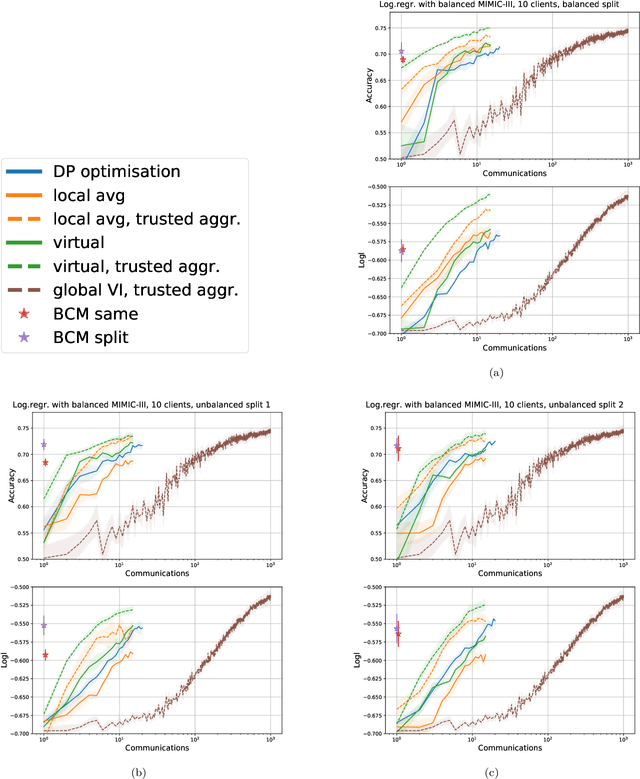
Learning a privacy-preserving model from distributed sensitive data is an increasingly important problem, often formulated in the federated learning context. Variational inference has recently been extended to the non-private federated learning setting via the partitioned variational inference algorithm. For privacy protection, the current gold standard is called differential privacy. Differential privacy guarantees privacy in a strong, mathematically clearly defined sense. In this paper, we present differentially private partitioned variational inference, the first general framework for learning a variational approximation to a Bayesian posterior distribution in the federated learning setting while minimising the number of communication rounds and providing differential privacy guarantees for data subjects. We propose three alternative implementations in the general framework, one based on perturbing local optimisation done by individual parties, and two based on perturbing global updates (one using a version of federated averaging, one adding virtual parties to the protocol), and compare their properties both theoretically and empirically. We show that perturbing the local optimisation works well with simple and complex models as long as each party has enough local data. However, the privacy is always guaranteed independently by each party. In contrast, perturbing the global updates works best with relatively simple models. Given access to suitable secure primitives, such as secure aggregation or secure shuffling, the performance can be improved by all parties guaranteeing privacy jointly.

Partitioned Variational Inference: A Framework for Probabilistic Federated Learning

The proliferation of computing devices has brought about an opportunity to deploy machine learning models on new problem domains using previously inaccessible data. Traditional algorithms for training such models often require data to be stored on a single machine with compute performed by a single node, making them unsuitable for decentralised training on multiple devices. This deficiency has motivated the development of federated learning algorithms, which allow multiple data owners to train collaboratively and use a shared model whilst keeping local data private. However, many of these algorithms focus on obtaining point estimates of model parameters, rather than probabilistic estimates capable of capturing model uncertainty, which is essential in many applications. Variational inference (VI) has become the method of choice for fitting many modern probabilistic models. In this paper we introduce partitioned variational inference (PVI), a general framework for performing VI in the federated setting. We develop new supporting theory for PVI, demonstrating a number of properties that make it an attractive choice for practitioners; use PVI to unify a wealth of fragmented, yet related literature; and provide empirical results that showcase the effectiveness of PVI in a variety of federated settings.

Do Concept Bottleneck Models Learn as Intended?

Concept bottleneck models map from raw inputs to concepts, and then from concepts to targets. Such models aim to incorporate pre-specified, high-level concepts into the learning procedure, and have been motivated to meet three desiderata: interpretability, predictability, and intervenability. However, we find that concept bottleneck models struggle to meet these goals. Using post hoc interpretability methods, we demonstrate that concepts do not correspond to anything semantically meaningful in input space, thus calling into question the usefulness of concept bottleneck models in their current form.

Sparse Gaussian Process Variational Autoencoders

Large, multi-dimensional spatio-temporal datasets are omnipresent in modern science and engineering. An effective framework for handling such data are Gaussian process deep generative models (GP-DGMs), which employ GP priors over the latent variables of DGMs. Existing approaches for performing inference in GP-DGMs do not support sparse GP approximations based on inducing points, which are essential for the computational efficiency of GPs, nor do they handle missing data -- a natural occurrence in many spatio-temporal datasets -- in a principled manner. We address these shortcomings with the development of the sparse Gaussian process variational autoencoder (SGP-VAE), characterised by the use of partial inference networks for parameterising sparse GP approximations. Leveraging the benefits of amortised variational inference, the SGP-VAE enables inference in multi-output sparse GPs on previously unobserved data with no additional training. The SGP-VAE is evaluated in a variety of experiments where it outperforms alternative approaches including multi-output GPs and structured VAEs.