Probabilistic Retrofitting of Learned Simulators

Dominant approaches for modelling Partial Differential Equations (PDEs) rely on deterministic predictions, yet many physical systems of interest are inherently chaotic and uncertain. While training probabilistic models from scratch is possible, it is computationally expensive and fails to leverage the significant resources already invested in high-performing deterministic backbones. In this work, we adopt a training-efficient strategy to transform pre-trained deterministic models into probabilistic ones via retrofitting with a proper scoring rule: the Continuous Ranked Probability Score (CRPS). Crucially, this approach is architecture-agnostic: it applies the same adaptation mechanism across distinct model backbones with minimal code modifications. The method proves highly effective across different scales of pre-training: for models trained on single dynamical systems, we achieve 20-54% reductions in rollout CRPS and up to 30% improvements in variance-normalised RMSE (VRMSE) relative to compute-matched deterministic fine-tuning. We further validate our approach on a PDE foundation model, trained on multiple systems and retrofitted on the dataset of interest, to show that our probabilistic adaptation yields an improvement of up to 40% in CRPS and up to 15% in VRMSE compared to deterministic fine-tuning. Validated across diverse architectures and dynamics, our results show that probabilistic PDE modelling need not require retraining from scratch, but can be unlocked from existing deterministic backbones with modest additional training cost.

Incremental Transformer Neural Processes

Neural Processes (NPs), and specifically Transformer Neural Processes (TNPs), have demonstrated remarkable performance across tasks ranging from spatiotemporal forecasting to tabular data modelling. However, many of these applications are inherently sequential, involving continuous data streams such as real-time sensor readings or database updates. In such settings, models should support cheap, incremental updates rather than recomputing internal representations from scratch for every new observation -- a capability existing TNP variants lack. Drawing inspiration from Large Language Models, we introduce the Incremental TNP (incTNP). By leveraging causal masking, Key-Value (KV) caching, and a data-efficient autoregressive training strategy, incTNP matches the predictive performance of standard TNPs while reducing the computational cost of updates from quadratic to linear time complexity. We empirically evaluate our model on a range of synthetic and real-world tasks, including tabular regression and temperature prediction. Our results show that, surprisingly, incTNP delivers performance comparable to -- or better than -- non-causal TNPs while unlocking orders-of-magnitude speedups for sequential inference. Finally, we assess the consistency of the model's updates -- by adapting a metric of ``implicit Bayesianness", we show that incTNP retains a prediction rule as implicitly Bayesian as standard non-causal TNPs, demonstrating that incTNP achieves the computational benefits of causal masking without sacrificing the consistency required for streaming inference.

Error Propagation and Model Collapse in Diffusion Models: A Theoretical Study

Machine learning models are increasingly trained or fine-tuned on synthetic data. Recursively training on such data has been observed to significantly degrade performance in a wide range of tasks, often characterized by a progressive drift away from the target distribution. In this work, we theoretically analyze this phenomenon in the setting of score-based diffusion models. For a realistic pipeline where each training round uses a combination of synthetic data and fresh samples from the target distribution, we obtain upper and lower bounds on the accumulated divergence between the generated and target distributions. This allows us to characterize different regimes of drift, depending on the score estimation error and the proportion of fresh data used in each generation. We also provide empirical results on synthetic data and images to illustrate the theory.

Probabilistic Modelling is Sufficient for Causal Inference

Causal inference is a key research area in machine learning, yet confusion reigns over the tools needed to tackle it. There are prevalent claims in the machine learning literature that you need a bespoke causal framework or notation to answer causal questions. In this paper, we want to make it clear that you \emph{can} answer any causal inference question within the realm of probabilistic modelling and inference, without causal-specific tools or notation. Through concrete examples, we demonstrate how causal questions can be tackled by writing down the probability of everything. Lastly, we reinterpret causal tools as emerging from standard probabilistic modelling and inference, elucidating their necessity and utility.

Wavelet-Induced Rotary Encodings: RoPE Meets Graphs

We introduce WIRE: Wavelet-Induced Rotary Encodings. WIRE extends Rotary Position Encodings (RoPE), a popular algorithm in LLMs and ViTs, to graph-structured data. We demonstrate that WIRE is more general than RoPE, recovering the latter in the special case of grid graphs. WIRE also enjoys a host of desirable theoretical properties, including equivariance under node ordering permutation, compatibility with linear attention, and (under select assumptions) asymptotic dependence on graph resistive distance. We test WIRE on a range of synthetic and real-world tasks, including identifying monochromatic subgraphs, semantic segmentation of point clouds, and more standard graph benchmarks. We find it to be effective in settings where the underlying graph structure is important.

Language models' activations linearly encode training-order recency

We show that language models' activations linearly encode when information was learned during training. Our setup involves creating a model with a known training order by sequentially fine-tuning Llama-3.2-1B on six disjoint but otherwise similar datasets about named entities. We find that the average activations of test samples for the six training datasets encode the training order: when projected into a 2D subspace, these centroids are arranged exactly in the order of training and lie on a straight line. Further, we show that linear probes can accurately (~90%) distinguish "early" vs. "late" entities, generalizing to entities unseen during the probes' own training. The model can also be fine-tuned to explicitly report an unseen entity's training stage (~80% accuracy). Interestingly, this temporal signal does not seem attributable to simple differences in activation magnitudes, losses, or model confidence. Our paper demonstrates that models are capable of differentiating information by its acquisition time, and carries significant implications for how they might manage conflicting data and respond to knowledge modifications.

Graph Random Features for Scalable Gaussian Processes

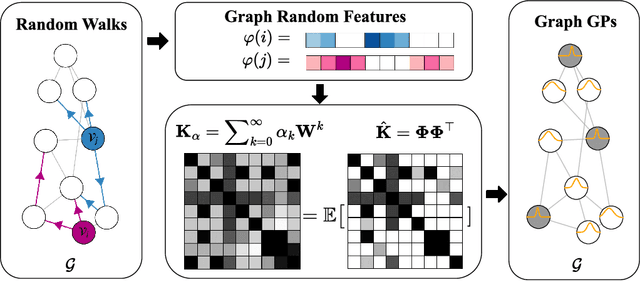
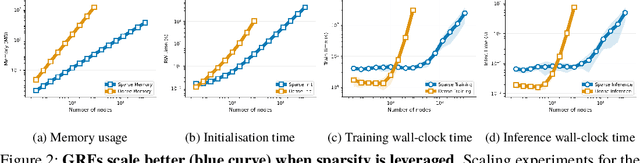
We study the application of graph random features (GRFs) - a recently introduced stochastic estimator of graph node kernels - to scalable Gaussian processes on discrete input spaces. We prove that (under mild assumptions) Bayesian inference with GRFs enjoys $O(N^{3/2})$ time complexity with respect to the number of nodes $N$, compared to $O(N^3)$ for exact kernels. Substantial wall-clock speedups and memory savings unlock Bayesian optimisation on graphs with over $10^6$ nodes on a single computer chip, whilst preserving competitive performance.

Distributional Training Data Attribution

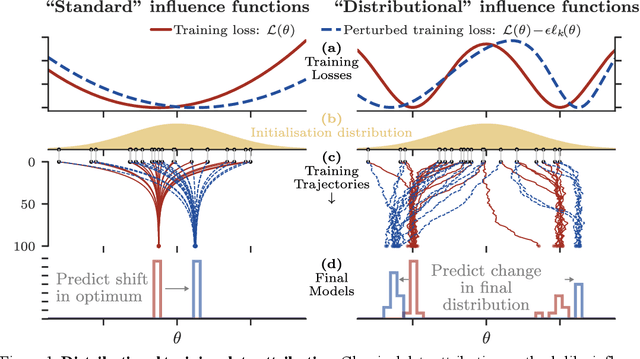
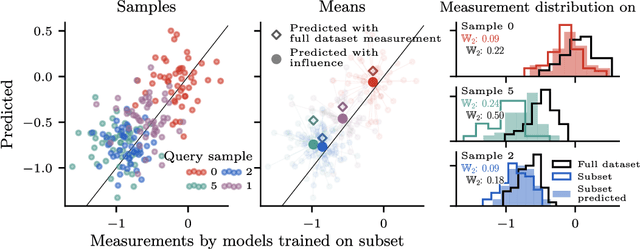
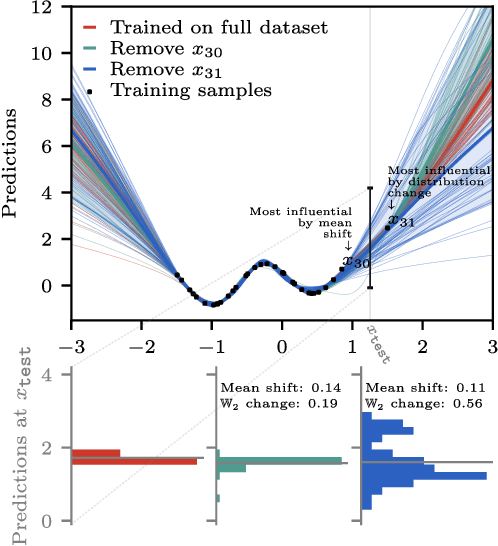
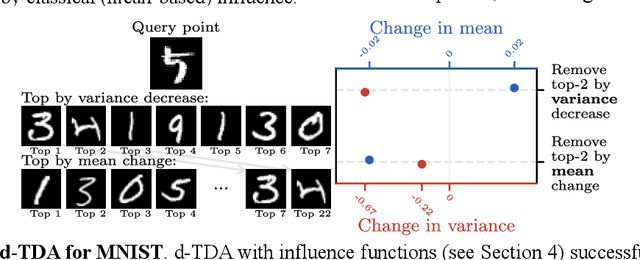
Randomness is an unavoidable part of training deep learning models, yet something that traditional training data attribution algorithms fail to rigorously account for. They ignore the fact that, due to stochasticity in the initialisation and batching, training on the same dataset can yield different models. In this paper, we address this shortcoming through introducing distributional training data attribution (d-TDA), the goal of which is to predict how the distribution of model outputs (over training runs) depends upon the dataset. We demonstrate the practical significance of d-TDA in experiments, e.g. by identifying training examples that drastically change the distribution of some target measurement without necessarily changing the mean. Intriguingly, we also find that influence functions (IFs), a popular but poorly-understood data attribution tool, emerge naturally from our distributional framework as the limit to unrolled differentiation; without requiring restrictive convexity assumptions. This provides a new mathematical motivation for their efficacy in deep learning, and helps to characterise their limitations.

JoLT: Joint Probabilistic Predictions on Tabular Data Using LLMs

We introduce a simple method for probabilistic predictions on tabular data based on Large Language Models (LLMs) called JoLT (Joint LLM Process for Tabular data). JoLT uses the in-context learning capabilities of LLMs to define joint distributions over tabular data conditioned on user-specified side information about the problem, exploiting the vast repository of latent problem-relevant knowledge encoded in LLMs. JoLT defines joint distributions for multiple target variables with potentially heterogeneous data types without any data conversion, data preprocessing, special handling of missing data, or model training, making it accessible and efficient for practitioners. Our experiments show that JoLT outperforms competitive methods on low-shot single-target and multi-target tabular classification and regression tasks. Furthermore, we show that JoLT can automatically handle missing data and perform data imputation by leveraging textual side information. We argue that due to its simplicity and generality, JoLT is an effective approach for a wide variety of real prediction problems.

Spectral-factorized Positive-definite Curvature Learning for NN Training

Many training methods, such as Adam(W) and Shampoo, learn a positive-definite curvature matrix and apply an inverse root before preconditioning. Recently, non-diagonal training methods, such as Shampoo, have gained significant attention; however, they remain computationally inefficient and are limited to specific types of curvature information due to the costly matrix root computation via matrix decomposition. To address this, we propose a Riemannian optimization approach that dynamically adapts spectral-factorized positive-definite curvature estimates, enabling the efficient application of arbitrary matrix roots and generic curvature learning. We demonstrate the efficacy and versatility of our approach in positive-definite matrix optimization and covariance adaptation for gradient-free optimization, as well as its efficiency in curvature learning for neural net training.