Decomposable Transformer Point Processes

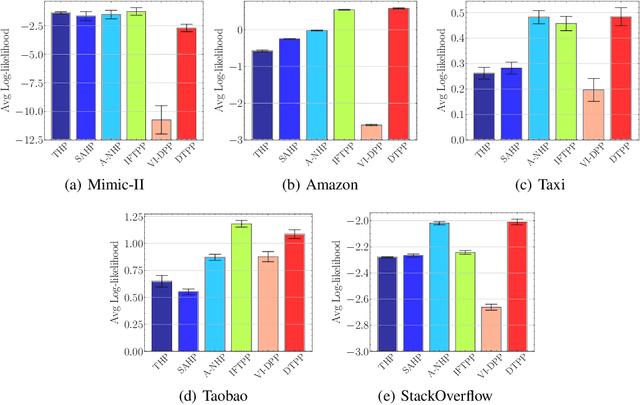
The standard paradigm of modeling marked point processes is by parameterizing the intensity function using an attention-based (Transformer-style) architecture. Despite the flexibility of these methods, their inference is based on the computationally intensive thinning algorithm. In this work, we propose a framework where the advantages of the attention-based architecture are maintained and the limitation of the thinning algorithm is circumvented. The framework depends on modeling the conditional distribution of inter-event times with a mixture of log-normals satisfying a Markov property and the conditional probability mass function for the marks with a Transformer-based architecture. The proposed method attains state-of-the-art performance in predicting the next event of a sequence given its history. The experiments also reveal the efficacy of the methods that do not rely on the thinning algorithm during inference over the ones they do. Finally, we test our method on the challenging long-horizon prediction task and find that it outperforms a baseline developed specifically for tackling this task; importantly, inference requires just a fraction of time compared to the thinning-based baseline.

Imperfect Vision Encoders: Efficient and Robust Tuning for Vision-Language Models

Vision language models (VLMs) demonstrate impressive capabilities in visual question answering and image captioning, acting as a crucial link between visual and language models. However, existing open-source VLMs heavily rely on pretrained and frozen vision encoders (such as CLIP). Despite CLIP's robustness across diverse domains, it still exhibits non-negligible image understanding errors. These errors propagate to the VLM responses, resulting in sub-optimal performance. In our work, we propose an efficient and robust method for updating vision encoders within VLMs. Our approach selectively and locally updates encoders, leading to substantial performance improvements on data where previous mistakes occurred, while maintaining overall robustness. Furthermore, we demonstrate the effectiveness of our method during continual few-shot updates. Theoretical grounding, generality, and computational efficiency characterize our approach.

First Session Adaptation: A Strong Replay-Free Baseline for Class-Incremental Learning

In Class-Incremental Learning (CIL) an image classification system is exposed to new classes in each learning session and must be updated incrementally. Methods approaching this problem have updated both the classification head and the feature extractor body at each session of CIL. In this work, we develop a baseline method, First Session Adaptation (FSA), that sheds light on the efficacy of existing CIL approaches and allows us to assess the relative performance contributions from head and body adaption. FSA adapts a pre-trained neural network body only on the first learning session and fixes it thereafter; a head based on linear discriminant analysis (LDA), is then placed on top of the adapted body, allowing exact updates through CIL. FSA is replay-free i.e.~it does not memorize examples from previous sessions of continual learning. To empirically motivate FSA, we first consider a diverse selection of 22 image-classification datasets, evaluating different heads and body adaptation techniques in high/low-shot offline settings. We find that the LDA head performs well and supports CIL out-of-the-box. We also find that Featurewise Layer Modulation (FiLM) adapters are highly effective in the few-shot setting, and full-body adaption in the high-shot setting. Second, we empirically investigate various CIL settings including high-shot CIL and few-shot CIL, including settings that have previously been used in the literature. We show that FSA significantly improves over the state-of-the-art in 15 of the 16 settings considered. FSA with FiLM adapters is especially performant in the few-shot setting. These results indicate that current approaches to continuous body adaptation are not working as expected. Finally, we propose a measure that can be applied to a set of unlabelled inputs which is predictive of the benefits of body adaptation.

How Good are Low-Rank Approximations in Gaussian Process Regression?

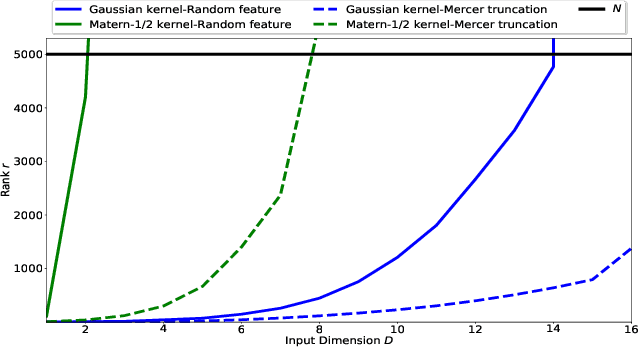
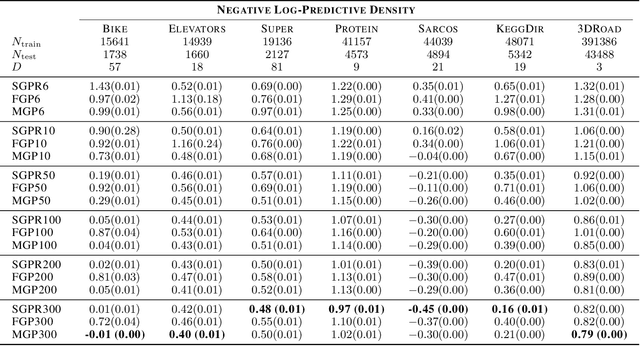
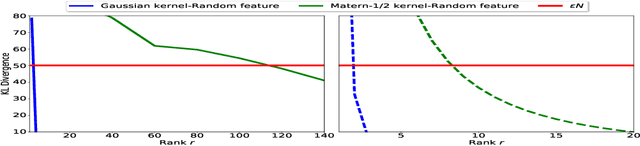
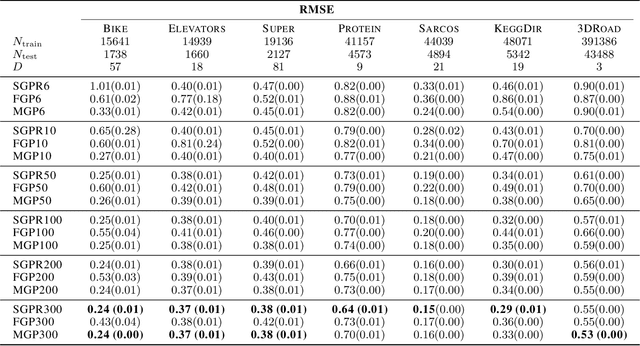
We provide guarantees for approximate Gaussian Process (GP) regression resulting from two common low-rank kernel approximations: based on random Fourier features, and based on truncating the kernel's Mercer expansion. In particular, we bound the Kullback-Leibler divergence between an exact GP and one resulting from one of the afore-described low-rank approximations to its kernel, as well as between their corresponding predictive densities, and we also bound the error between predictive mean vectors and between predictive covariance matrices computed using the exact versus using the approximate GP. We provide experiments on both simulated data and standard benchmarks to evaluate the effectiveness of our theoretical bounds.

Scalable and Interpretable Marked Point Processes

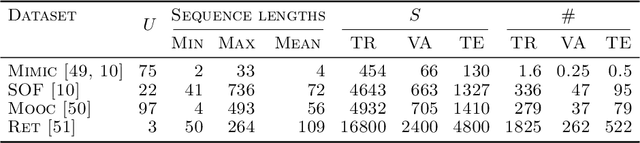
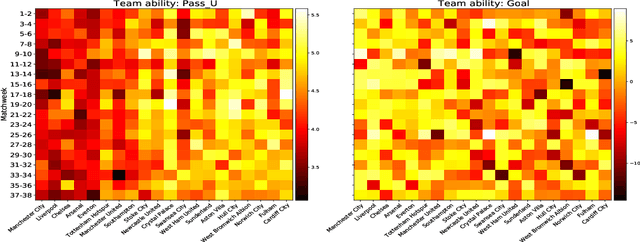
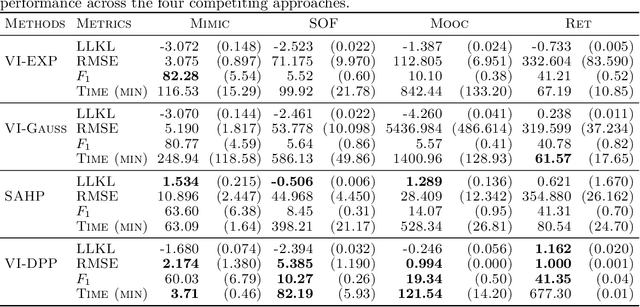
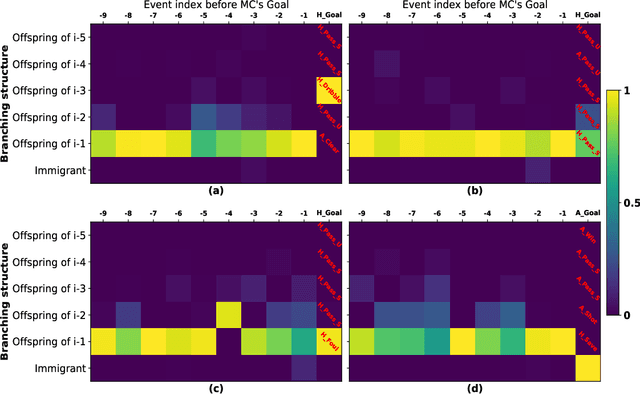
We introduce a novel inferential framework for marked point processes that enjoys both scalability and interpretability. The framework is based on variational inference and it aims to speed up inference for a flexible family of marked point processes where the joint distribution of times and marks can be specified in terms of the conditional distribution of times given the process filtration, and of the conditional distribution of marks given the process filtration and the current time. We assess the predictive ability of our proposed method over four real-world datasets where results show its competitive performance against other baselines. The attractiveness of our framework for the modelling of marked point processes is illustrated through a case study of association football data where scalability and interpretability are exploited for extracting useful informative patterns.

Faster Gaussian Processes via Deep Embeddings

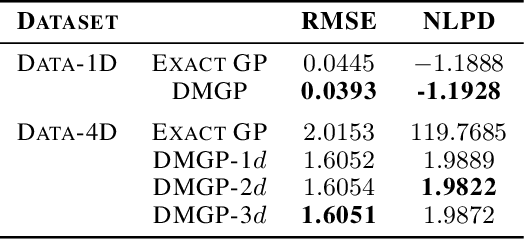
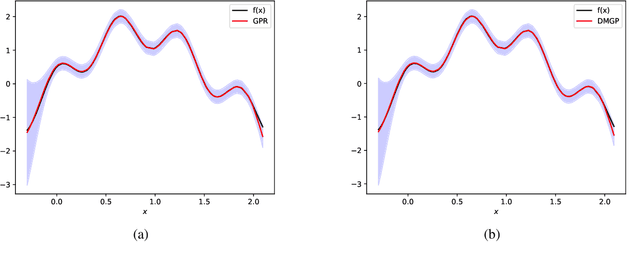
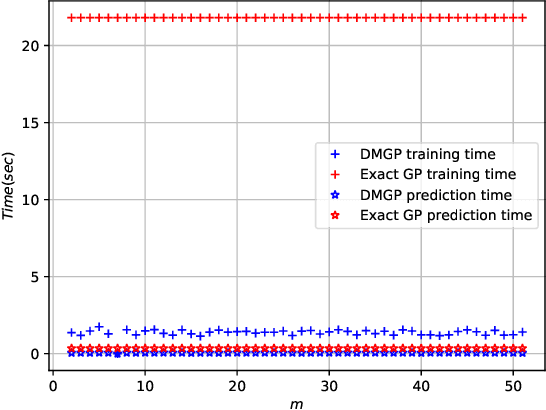
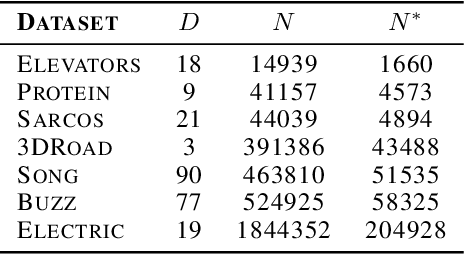
Gaussian processes provide a probabilistic framework for quantifying uncertainty of prediction and have been adopted in many applications in Statistics and Bayesian optimization. Unfortunately, they are hard to scale to large datasets as they necessitate inverting matrices whose size is linear in the number of observations. Moreover, they necessitate an a priori chosen functional form for their kernels with predetermined features. Our contribution is a framework that addresses both challenges. We use deep neural networks for automatic feature extraction, combined with explicit functional forms for the eigenspectrum of Gaussian processes with Gaussian kernels, to derive a Gaussian process inference and prediction framework whose complexity scales linearly in the number of observations and which accommodates automatic feature extraction. On a series of datasets, our method outperforms state of the art scalable Gaussian process approximations.

Fully Scalable Gaussian Processes using Subspace Inducing Inputs

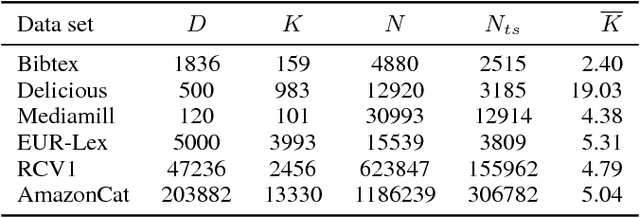
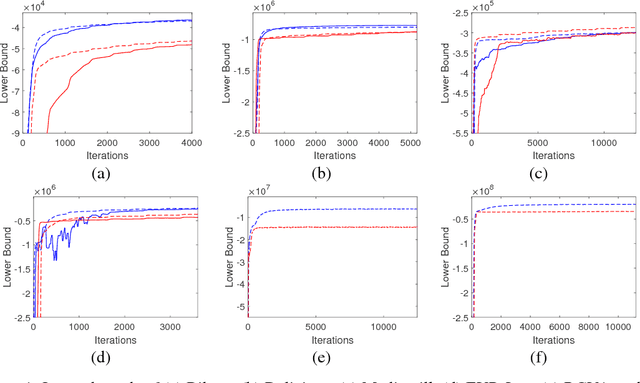
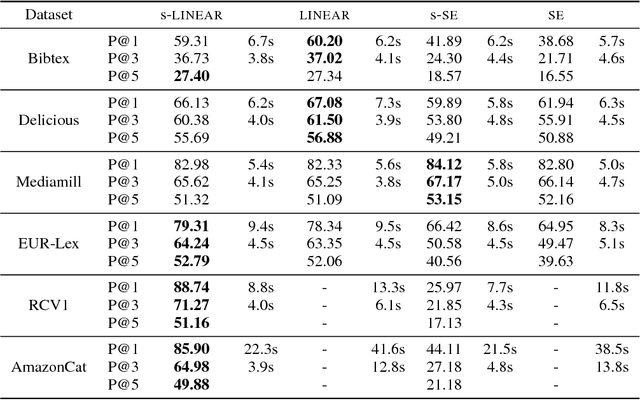
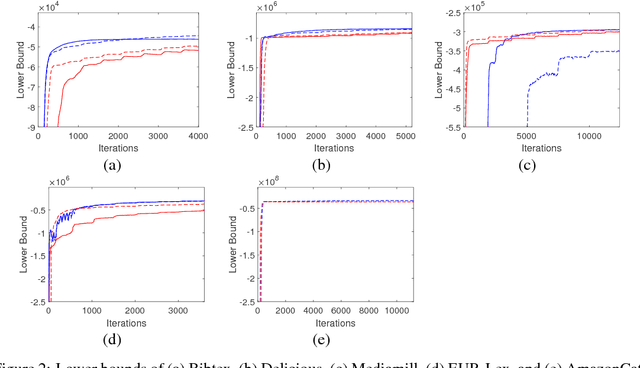
We introduce fully scalable Gaussian processes, an implementation scheme that tackles the problem of treating a high number of training instances together with high dimensional input data. Our key idea is a representation trick over the inducing variables called subspace inducing inputs. This is combined with certain matrix-preconditioning based parametrizations of the variational distributions that lead to simplified and numerically stable variational lower bounds. Our illustrative applications are based on challenging extreme multi-label classification problems with the extra burden of the very large number of class labels. We demonstrate the usefulness of our approach by presenting predictive performances together with low computational times in datasets with extremely large number of instances and input dimensions.