Can independent Metropolis beat crude Monte Carlo?

Assume that we would like to estimate the expected value of a function $F$ with respect to a density $\pi$. We prove that if $\pi$ is close enough under KL divergence to another density $q$, an independent Metropolis sampler estimator that obtains samples from $\pi$ with proposal density $q$, enriched with a variance reduction computational strategy based on control variates, achieves smaller asymptotic variance than that of the crude Monte Carlo estimator. The control variates construction requires no extra computational effort but assumes that the expected value of $F$ under $q$ is analytically available. We illustrate this result by calculating the marginal likelihood in a linear regression model with prior-likelihood conflict and a non-conjugate prior. Furthermore, we propose an adaptive independent Metropolis algorithm that adapts the proposal density such that its KL divergence with the target is being reduced. We demonstrate its applicability in a Bayesian logistic and Gaussian process regression problems and we rigorously justify our asymptotic arguments under easily verifiable and essentially minimal conditions.

Probabilistic Multi-Layer Perceptrons for Wind Farm Condition Monitoring

We provide a condition monitoring system for wind farms, based on normal behaviour modelling using a probabilistic multi-layer perceptron with transfer learning via fine-tuning. The model predicts the output power of the wind turbine under normal behaviour based on features retrieved from supervisory control and data acquisition (SCADA) systems. Its advantages are that (i) it can be trained with SCADA data of at least a few years, (ii) it can incorporate all SCADA data of all wind turbines in a wind farm as features, (iii) it assumes that the output power follows a normal density with heteroscedastic variance and (iv) it can predict the output of one wind turbine by borrowing strength from the data of all other wind turbines in a farm. Probabilistic guidelines for condition monitoring are given via a CUSUM control chart. We illustrate the performance of our model in a real SCADA data example which provides evidence that it outperforms other probabilistic prediction models.

Learning variational autoencoders via MCMC speed measures

Variational autoencoders (VAEs) are popular likelihood-based generative models which can be efficiently trained by maximizing an Evidence Lower Bound (ELBO). There has been much progress in improving the expressiveness of the variational distribution to obtain tighter variational bounds and increased generative performance. Whilst previous work has leveraged Markov chain Monte Carlo (MCMC) methods for the construction of variational densities, gradient-based methods for adapting the proposal distributions for deep latent variable models have received less attention. This work suggests an entropy-based adaptation for a short-run Metropolis-adjusted Langevin (MALA) or Hamiltonian Monte Carlo (HMC) chain while optimising a tighter variational bound to the log-evidence. Experiments show that this approach yields higher held-out log-likelihoods as well as improved generative metrics. Our implicit variational density can adapt to complicated posterior geometries of latent hierarchical representations arising in hierarchical VAEs.

How Good are Low-Rank Approximations in Gaussian Process Regression?

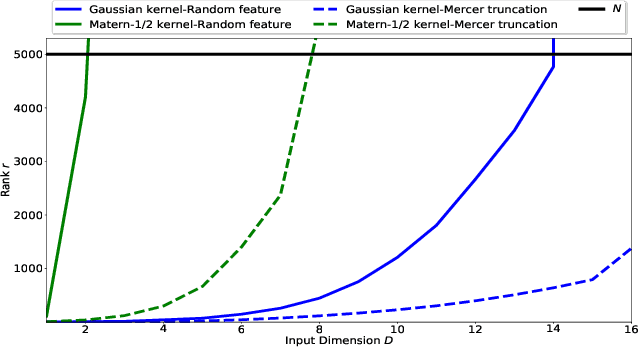
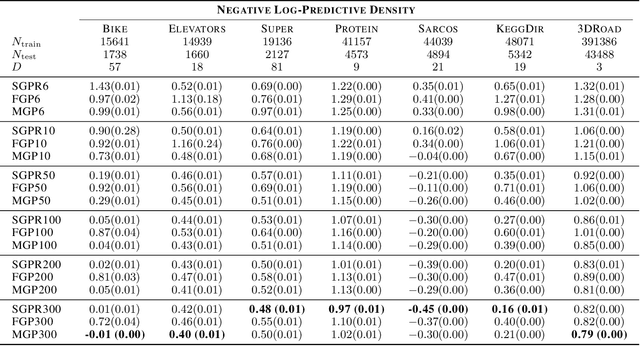
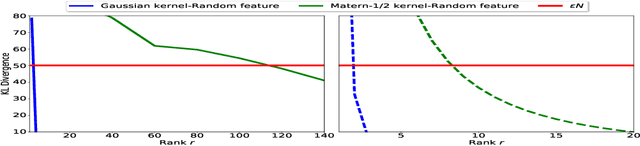
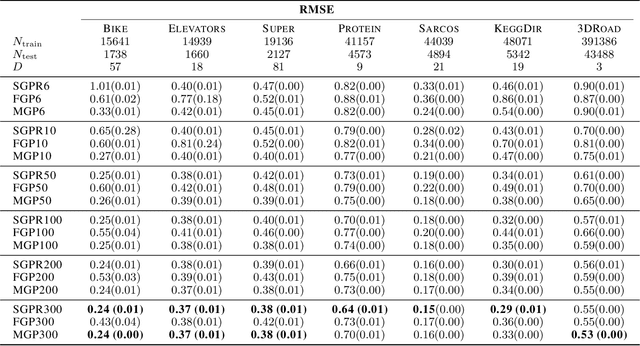
We provide guarantees for approximate Gaussian Process (GP) regression resulting from two common low-rank kernel approximations: based on random Fourier features, and based on truncating the kernel's Mercer expansion. In particular, we bound the Kullback-Leibler divergence between an exact GP and one resulting from one of the afore-described low-rank approximations to its kernel, as well as between their corresponding predictive densities, and we also bound the error between predictive mean vectors and between predictive covariance matrices computed using the exact versus using the approximate GP. We provide experiments on both simulated data and standard benchmarks to evaluate the effectiveness of our theoretical bounds.

Entropy-based adaptive Hamiltonian Monte Carlo

Hamiltonian Monte Carlo (HMC) is a popular Markov Chain Monte Carlo (MCMC) algorithm to sample from an unnormalized probability distribution. A leapfrog integrator is commonly used to implement HMC in practice, but its performance can be sensitive to the choice of mass matrix used therein. We develop a gradient-based algorithm that allows for the adaptation of the mass matrix by encouraging the leapfrog integrator to have high acceptance rates while also exploring all dimensions jointly. In contrast to previous work that adapt the hyperparameters of HMC using some form of expected squared jumping distance, the adaptation strategy suggested here aims to increase sampling efficiency by maximizing an approximation of the proposal entropy. We illustrate that using multiple gradients in the HMC proposal can be beneficial compared to a single gradient-step in Metropolis-adjusted Langevin proposals. Empirical evidence suggests that the adaptation method can outperform different versions of HMC schemes by adjusting the mass matrix to the geometry of the target distribution and by providing some control on the integration time.

Scalable and Interpretable Marked Point Processes

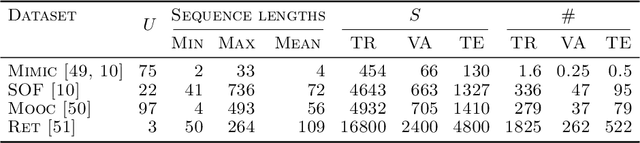
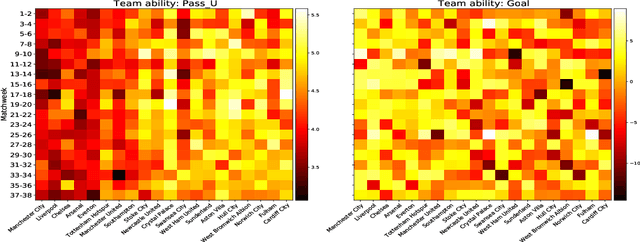
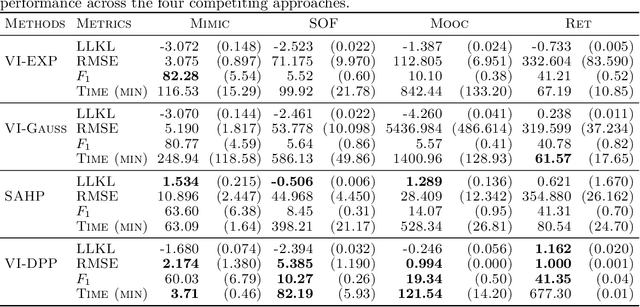
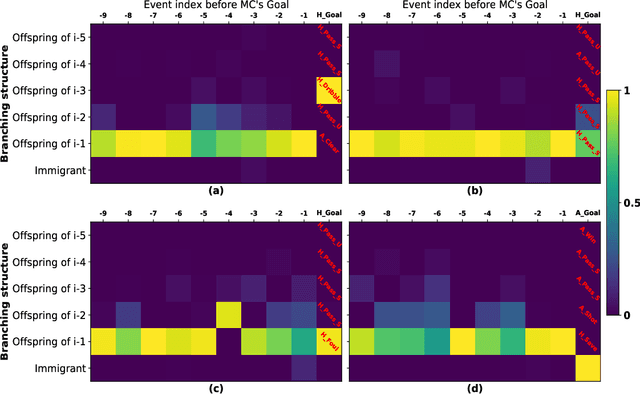
We introduce a novel inferential framework for marked point processes that enjoys both scalability and interpretability. The framework is based on variational inference and it aims to speed up inference for a flexible family of marked point processes where the joint distribution of times and marks can be specified in terms of the conditional distribution of times given the process filtration, and of the conditional distribution of marks given the process filtration and the current time. We assess the predictive ability of our proposed method over four real-world datasets where results show its competitive performance against other baselines. The attractiveness of our framework for the modelling of marked point processes is illustrated through a case study of association football data where scalability and interpretability are exploited for extracting useful informative patterns.

Faster Gaussian Processes via Deep Embeddings

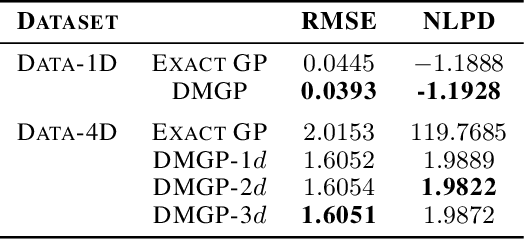
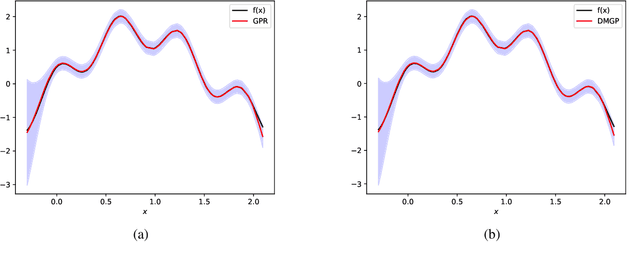
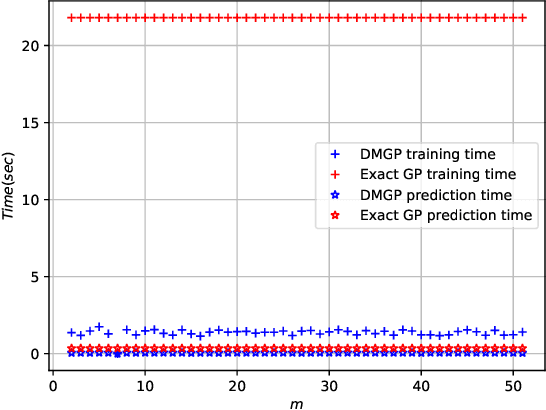
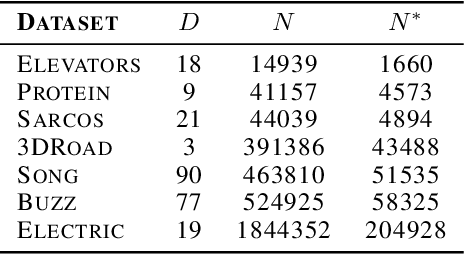
Gaussian processes provide a probabilistic framework for quantifying uncertainty of prediction and have been adopted in many applications in Statistics and Bayesian optimization. Unfortunately, they are hard to scale to large datasets as they necessitate inverting matrices whose size is linear in the number of observations. Moreover, they necessitate an a priori chosen functional form for their kernels with predetermined features. Our contribution is a framework that addresses both challenges. We use deep neural networks for automatic feature extraction, combined with explicit functional forms for the eigenspectrum of Gaussian processes with Gaussian kernels, to derive a Gaussian process inference and prediction framework whose complexity scales linearly in the number of observations and which accommodates automatic feature extraction. On a series of datasets, our method outperforms state of the art scalable Gaussian process approximations.

Gradient-based Adaptive Markov Chain Monte Carlo

We introduce a gradient-based learning method to automatically adapt Markov chain Monte Carlo (MCMC) proposal distributions to intractable targets. We define a maximum entropy regularised objective function, referred to as generalised speed measure, which can be robustly optimised over the parameters of the proposal distribution by applying stochastic gradient optimisation. An advantage of our method compared to traditional adaptive MCMC methods is that the adaptation occurs even when candidate state values are rejected. This is a highly desirable property of any adaptation strategy because the adaptation starts in early iterations even if the initial proposal distribution is far from optimum. We apply the framework for learning multivariate random walk Metropolis and Metropolis-adjusted Langevin proposals with full covariance matrices, and provide empirical evidence that our method can outperform other MCMC algorithms, including Hamiltonian Monte Carlo schemes.

Copula-like Variational Inference

This paper considers a new family of variational distributions motivated by Sklar's theorem. This family is based on new copula-like densities on the hypercube with non-uniform marginals which can be sampled efficiently, i.e. with a complexity linear in the dimension of state space. Then, the proposed variational densities that we suggest can be seen as arising from these copula-like densities used as base distributions on the hypercube with Gaussian quantile functions and sparse rotation matrices as normalizing flows. The latter correspond to a rotation of the marginals with complexity $\mathcal{O}(d \log d)$. We provide some empirical evidence that such a variational family can also approximate non-Gaussian posteriors and can be beneficial compared to Gaussian approximations. Our method performs largely comparably to state-of-the-art variational approximations on standard regression and classification benchmarks for Bayesian Neural Networks.

Scalable Bayesian Learning for State Space Models using Variational Inference with SMC Samplers

We present a scalable approach to performing approximate fully Bayesian inference in generic state space models. The proposed method is an alternative to particle MCMC that provides fully Bayesian inference of both the dynamic latent states and the static parameters of the model. We build up on recent advances in computational statistics that combine variational methods with sequential Monte Carlo sampling and we demonstrate the advantages of performing full Bayesian inference over the static parameters rather than just performing variational EM approximations. We illustrate how our approach enables scalable inference in multivariate stochastic volatility models and self-exciting point process models that allow for flexible dynamics in the latent intensity function.