Sparse Gaussian Processes: Structured Approximations and Power-EP Revisited

Inducing-point-based sparse variational Gaussian processes have become the standard workhorse for scaling up GP models. Recent advances show that these methods can be improved by introducing a diagonal scaling matrix to the conditional posterior density given the inducing points. This paper first considers an extension that employs a block-diagonal structure for the scaling matrix, provably tightening the variational lower bound. We then revisit the unifying framework of sparse GPs based on Power Expectation Propagation (PEP) and show that it can leverage and benefit from the new structured approximate posteriors. Through extensive regression experiments, we show that the proposed block-diagonal approximation consistently performs similarly to or better than existing diagonal approximations while maintaining comparable computational costs. Furthermore, the new PEP framework with structured posteriors provides competitive performance across various power hyperparameter settings, offering practitioners flexible alternatives to standard variational approaches.

Gaussian Invariant Markov Chain Monte Carlo

We develop sampling methods, which consist of Gaussian invariant versions of random walk Metropolis (RWM), Metropolis adjusted Langevin algorithm (MALA) and second order Hessian or Manifold MALA. Unlike standard RWM and MALA we show that Gaussian invariant sampling can lead to ergodic estimators with improved statistical efficiency. This is due to a remarkable property of Gaussian invariance that allows us to obtain exact analytical solutions to the Poisson equation for Gaussian targets. These solutions can be used to construct efficient and easy to use control variates for variance reduction of estimators under any intractable target. We demonstrate the new samplers and estimators in several examples, including high dimensional targets in latent Gaussian models where we compare against several advanced methods and obtain state-of-the-art results. We also provide theoretical results regarding geometric ergodicity, and an optimal scaling analysis that shows the dependence of the optimal acceptance rate on the Gaussianity of the target.

Learning-Order Autoregressive Models with Application to Molecular Graph Generation

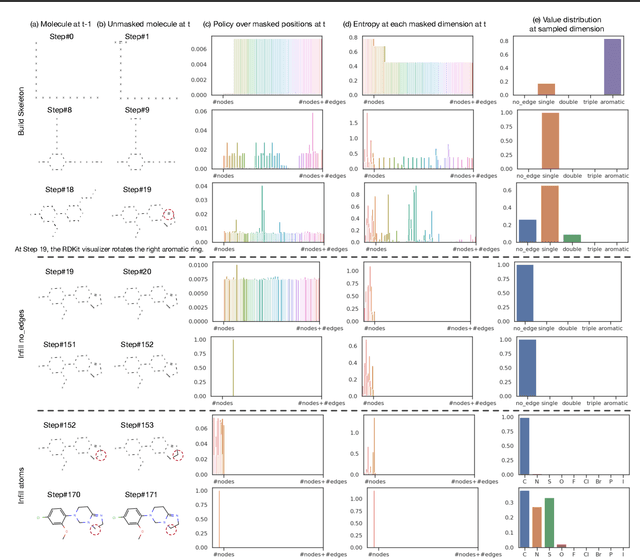
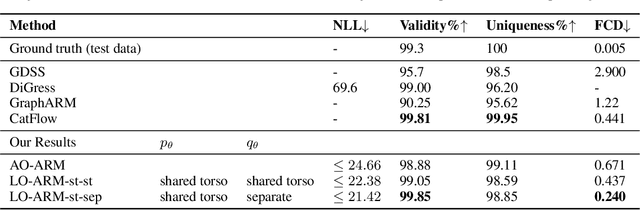
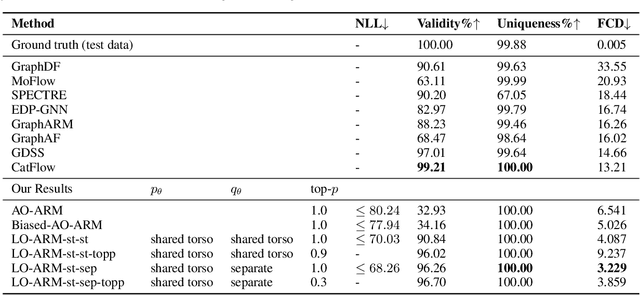
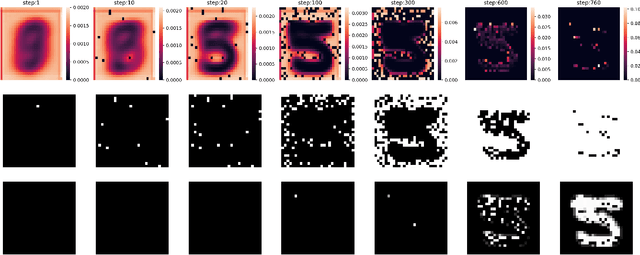
Autoregressive models (ARMs) have become the workhorse for sequence generation tasks, since many problems can be modeled as next-token prediction. While there appears to be a natural ordering for text (i.e., left-to-right), for many data types, such as graphs, the canonical ordering is less obvious. To address this problem, we introduce a variant of ARM that generates high-dimensional data using a probabilistic ordering that is sequentially inferred from data. This model incorporates a trainable probability distribution, referred to as an \emph{order-policy}, that dynamically decides the autoregressive order in a state-dependent manner. To train the model, we introduce a variational lower bound on the exact log-likelihood, which we optimize with stochastic gradient estimation. We demonstrate experimentally that our method can learn meaningful autoregressive orderings in image and graph generation. On the challenging domain of molecular graph generation, we achieve state-of-the-art results on the QM9 and ZINC250k benchmarks, evaluated using the Fr\'{e}chet ChemNet Distance (FCD).

New Bounds for Sparse Variational Gaussian Processes

Sparse variational Gaussian processes (GPs) construct tractable posterior approximations to GP models. At the core of these methods is the assumption that the true posterior distribution over training function values ${\bf f}$ and inducing variables ${\bf u}$ is approximated by a variational distribution that incorporates the conditional GP prior $p({\bf f} | {\bf u})$ in its factorization. While this assumption is considered as fundamental, we show that for model training we can relax it through the use of a more general variational distribution $q({\bf f} | {\bf u})$ that depends on $N$ extra parameters, where $N$ is the number of training examples. In GP regression, we can analytically optimize the evidence lower bound over the extra parameters and express a tractable collapsed bound that is tighter than the previous bound. The new bound is also amenable to stochastic optimization and its implementation requires minor modifications to existing sparse GP code. Further, we also describe extensions to non-Gaussian likelihoods. On several datasets we demonstrate that our method can reduce bias when learning the hyperpaparameters and can lead to better predictive performance.

Non-Stationary Learning of Neural Networks with Automatic Soft Parameter Reset

Neural networks are traditionally trained under the assumption that data come from a stationary distribution. However, settings which violate this assumption are becoming more popular; examples include supervised learning under distributional shifts, reinforcement learning, continual learning and non-stationary contextual bandits. In this work we introduce a novel learning approach that automatically models and adapts to non-stationarity, via an Ornstein-Uhlenbeck process with an adaptive drift parameter. The adaptive drift tends to draw the parameters towards the initialisation distribution, so the approach can be understood as a form of soft parameter reset. We show empirically that our approach performs well in non-stationary supervised and off-policy reinforcement learning settings.

Can independent Metropolis beat crude Monte Carlo?

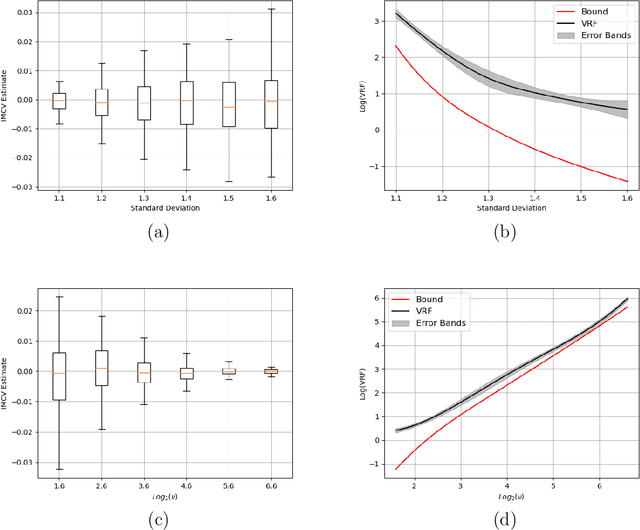
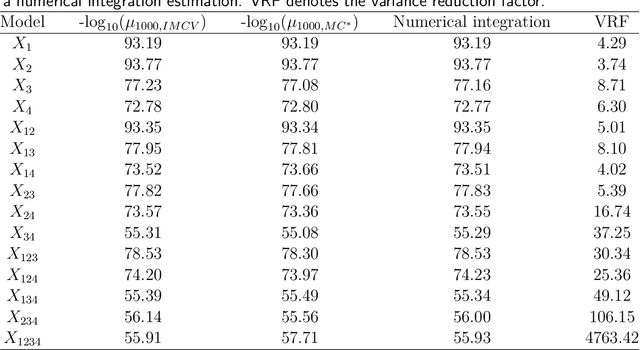
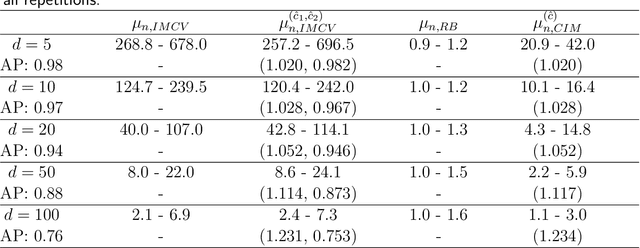
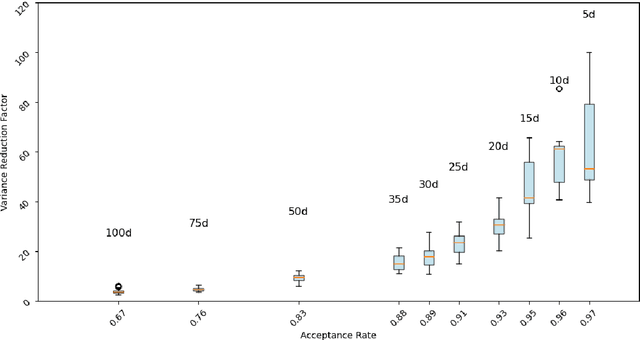
Assume that we would like to estimate the expected value of a function $F$ with respect to a density $\pi$. We prove that if $\pi$ is close enough under KL divergence to another density $q$, an independent Metropolis sampler estimator that obtains samples from $\pi$ with proposal density $q$, enriched with a variance reduction computational strategy based on control variates, achieves smaller asymptotic variance than that of the crude Monte Carlo estimator. The control variates construction requires no extra computational effort but assumes that the expected value of $F$ under $q$ is analytically available. We illustrate this result by calculating the marginal likelihood in a linear regression model with prior-likelihood conflict and a non-conjugate prior. Furthermore, we propose an adaptive independent Metropolis algorithm that adapts the proposal density such that its KL divergence with the target is being reduced. We demonstrate its applicability in a Bayesian logistic and Gaussian process regression problems and we rigorously justify our asymptotic arguments under easily verifiable and essentially minimal conditions.

Simplified and Generalized Masked Diffusion for Discrete Data

Masked (or absorbing) diffusion is actively explored as an alternative to autoregressive models for generative modeling of discrete data. However, existing work in this area has been hindered by unnecessarily complex model formulations and unclear relationships between different perspectives, leading to suboptimal parameterization, training objectives, and ad hoc adjustments to counteract these issues. In this work, we aim to provide a simple and general framework that unlocks the full potential of masked diffusion models. We show that the continuous-time variational objective of masked diffusion models is a simple weighted integral of cross-entropy losses. Our framework also enables training generalized masked diffusion models with state-dependent masking schedules. When evaluated by perplexity, our models trained on OpenWebText surpass prior diffusion language models at GPT-2 scale and demonstrate superior performance on 4 out of 5 zero-shot language modeling tasks. Furthermore, our models vastly outperform previous discrete diffusion models on pixel-level image modeling, achieving 2.78~(CIFAR-10) and 3.42 (ImageNet 64$\times$64) bits per dimension that are comparable or better than autoregressive models of similar sizes.

Revisiting Dynamic Evaluation: Online Adaptation for Large Language Models

We consider the problem of online fine tuning the parameters of a language model at test time, also known as dynamic evaluation. While it is generally known that this approach improves the overall predictive performance, especially when considering distributional shift between training and evaluation data, we here emphasize the perspective that online adaptation turns parameters into temporally changing states and provides a form of context-length extension with memory in weights, more in line with the concept of memory in neuroscience. We pay particular attention to the speed of adaptation (in terms of sample efficiency),sensitivity to the overall distributional drift, and the computational overhead for performing gradient computations and parameter updates. Our empirical study provides insights on when online adaptation is particularly interesting. We highlight that with online adaptation the conceptual distinction between in-context learning and fine tuning blurs: both are methods to condition the model on previously observed tokens.

Kalman Filter for Online Classification of Non-Stationary Data

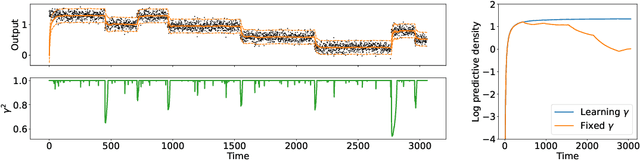
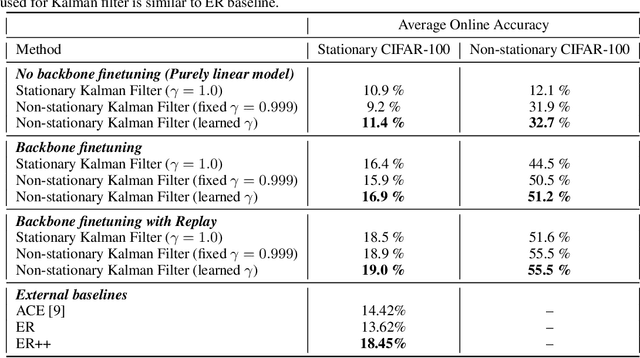
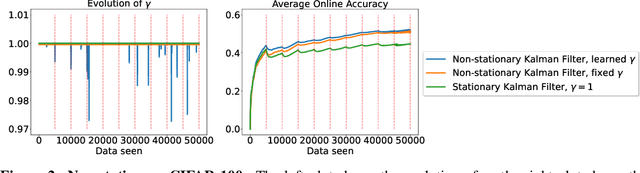
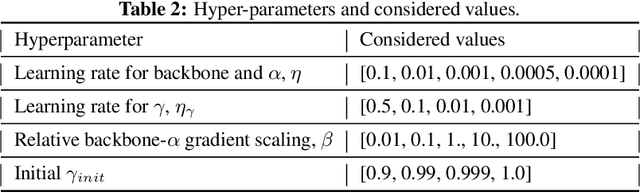
In Online Continual Learning (OCL) a learning system receives a stream of data and sequentially performs prediction and training steps. Important challenges in OCL are concerned with automatic adaptation to the particular non-stationary structure of the data, and with quantification of predictive uncertainty. Motivated by these challenges we introduce a probabilistic Bayesian online learning model by using a (possibly pretrained) neural representation and a state space model over the linear predictor weights. Non-stationarity over the linear predictor weights is modelled using a parameter drift transition density, parametrized by a coefficient that quantifies forgetting. Inference in the model is implemented with efficient Kalman filter recursions which track the posterior distribution over the linear weights, while online SGD updates over the transition dynamics coefficient allows to adapt to the non-stationarity seen in data. While the framework is developed assuming a linear Gaussian model, we also extend it to deal with classification problems and for fine-tuning the deep learning representation. In a set of experiments in multi-class classification using data sets such as CIFAR-100 and CLOC we demonstrate the predictive ability of the model and its flexibility to capture non-stationarity.

Optimal Preconditioning and Fisher Adaptive Langevin Sampling

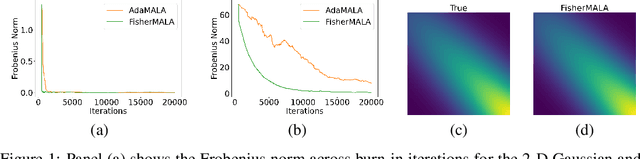
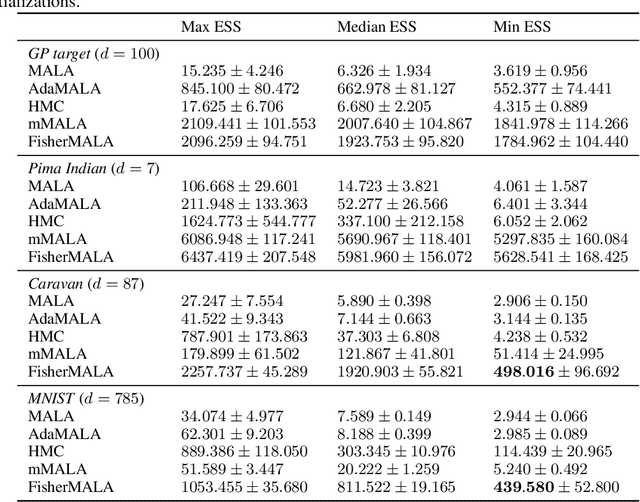
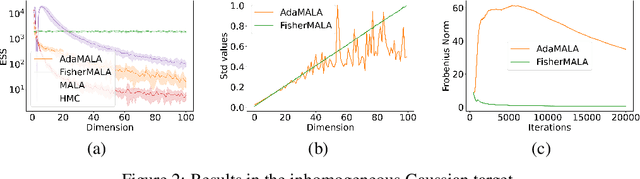
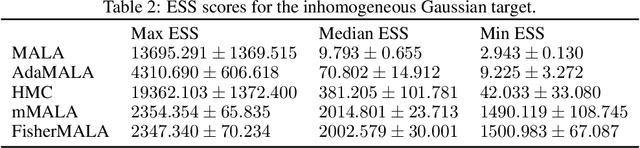
We define an optimal preconditioning for the Langevin diffusion by analytically maximizing the expected squared jumped distance. This yields as the optimal preconditioning an inverse Fisher information covariance matrix, where the covariance matrix is computed as the outer product of log target gradients averaged under the target. We apply this result to the Metropolis adjusted Langevin algorithm (MALA) and derive a computationally efficient adaptive MCMC scheme that learns the preconditioning from the history of gradients produced as the algorithm runs. We show in several experiments that the proposed algorithm is very robust in high dimensions and significantly outperforms other methods, including a closely related adaptive MALA scheme that learns the preconditioning with standard adaptive MCMC as well as the position-dependent Riemannian manifold MALA sampler.