Non-Stationary Learning of Neural Networks with Automatic Soft Parameter Reset

Neural networks are traditionally trained under the assumption that data come from a stationary distribution. However, settings which violate this assumption are becoming more popular; examples include supervised learning under distributional shifts, reinforcement learning, continual learning and non-stationary contextual bandits. In this work we introduce a novel learning approach that automatically models and adapts to non-stationarity, via an Ornstein-Uhlenbeck process with an adaptive drift parameter. The adaptive drift tends to draw the parameters towards the initialisation distribution, so the approach can be understood as a form of soft parameter reset. We show empirically that our approach performs well in non-stationary supervised and off-policy reinforcement learning settings.

Toward Understanding In-context vs. In-weight Learning

It has recently been demonstrated empirically that in-context learning emerges in transformers when certain distributional properties are present in the training data, but this ability can also diminish upon further training. We provide a new theoretical understanding of these phenomena by identifying simplified distributional properties that give rise to the emergence and eventual disappearance of in-context learning. We do so by first analyzing a simplified model that uses a gating mechanism to choose between an in-weight and an in-context predictor. Through a combination of a generalization error and regret analysis we identify conditions where in-context and in-weight learning emerge. These theoretical findings are then corroborated experimentally by comparing the behaviour of a full transformer on the simplified distributions to that of the stylized model, demonstrating aligned results. We then extend the study to a full large language model, showing how fine-tuning on various collections of natural language prompts can elicit similar in-context and in-weight learning behaviour.

Learning Continually by Spectral Regularization

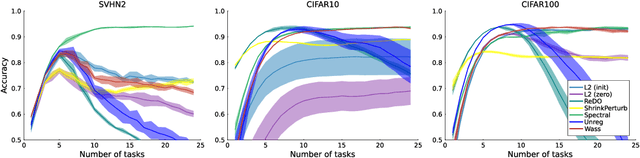
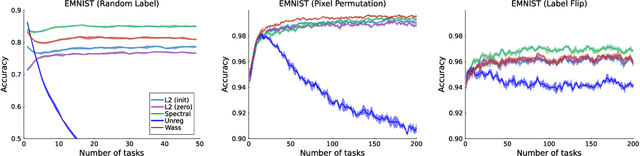
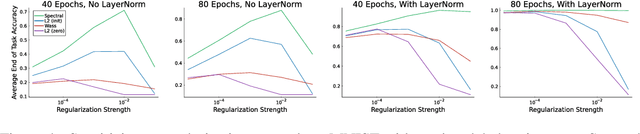
Loss of plasticity is a phenomenon where neural networks become more difficult to train during the course of learning. Continual learning algorithms seek to mitigate this effect by sustaining good predictive performance while maintaining network trainability. We develop new techniques for improving continual learning by first reconsidering how initialization can ensure trainability during early phases of learning. From this perspective, we derive new regularization strategies for continual learning that ensure beneficial initialization properties are better maintained throughout training. In particular, we investigate two new regularization techniques for continual learning: (i) Wasserstein regularization toward the initial weight distribution, which is less restrictive than regularizing toward initial weights; and (ii) regularizing weight matrix singular values, which directly ensures gradient diversity is maintained throughout training. We present an experimental analysis that shows these alternative regularizers can improve continual learning performance across a range of supervised learning tasks and model architectures. The alternative regularizers prove to be less sensitive to hyperparameters while demonstrating better training in individual tasks, sustaining trainability as new tasks arrive, and achieving better generalization performance.

Prior-Dependent Allocations for Bayesian Fixed-Budget Best-Arm Identification in Structured Bandits

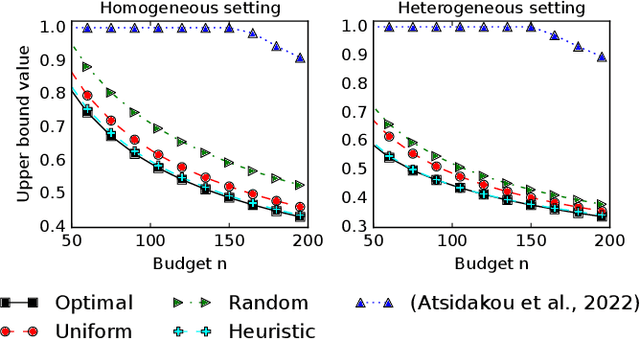
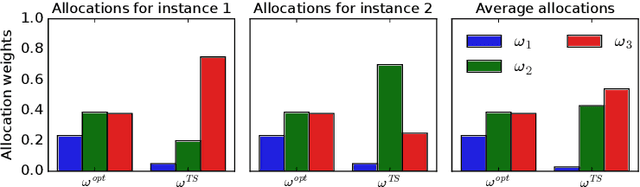
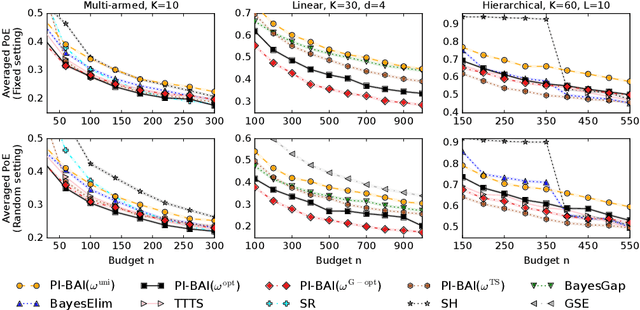
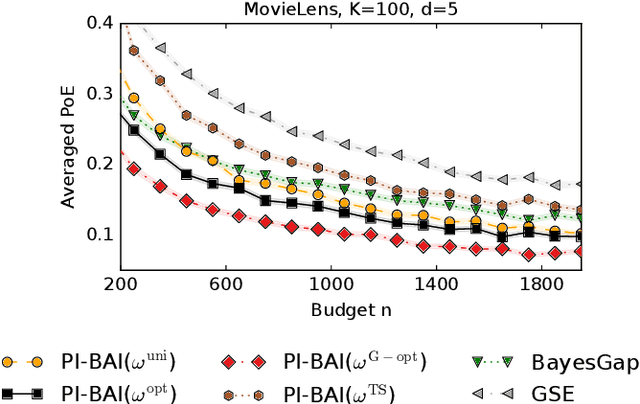
We study the problem of Bayesian fixed-budget best-arm identification (BAI) in structured bandits. We propose an algorithm that uses fixed allocations based on the prior information and the structure of the environment. We provide theoretical bounds on its performance across diverse models, including the first prior-dependent upper bounds for linear and hierarchical BAI. Our key contribution is introducing new proof methods that result in tighter bounds for multi-armed BAI compared to existing methods. We extensively compare our approach to other fixed-budget BAI methods, demonstrating its consistent and robust performance in various settings. Our work improves our understanding of Bayesian fixed-budget BAI in structured bandits and highlights the effectiveness of our approach in practical scenarios.

Online RL in Linearly $q^π$-Realizable MDPs Is as Easy as in Linear MDPs If You Learn What to Ignore

We consider online reinforcement learning (RL) in episodic Markov decision processes (MDPs) under the linear $q^\pi$-realizability assumption, where it is assumed that the action-values of all policies can be expressed as linear functions of state-action features. This class is known to be more general than linear MDPs, where the transition kernel and the reward function are assumed to be linear functions of the feature vectors. As our first contribution, we show that the difference between the two classes is the presence of states in linearly $q^\pi$-realizable MDPs where for any policy, all the actions have approximately equal values, and skipping over these states by following an arbitrarily fixed policy in those states transforms the problem to a linear MDP. Based on this observation, we derive a novel (computationally inefficient) learning algorithm for linearly $q^\pi$-realizable MDPs that simultaneously learns what states should be skipped over and runs another learning algorithm on the linear MDP hidden in the problem. The method returns an $\epsilon$-optimal policy after $\text{polylog}(H, d)/\epsilon^2$ interactions with the MDP, where $H$ is the time horizon and $d$ is the dimension of the feature vectors, giving the first polynomial-sample-complexity online RL algorithm for this setting. The results are proved for the misspecified case, where the sample complexity is shown to degrade gracefully with the misspecification error.

Optimistic Natural Policy Gradient: a Simple Efficient Policy Optimization Framework for Online RL

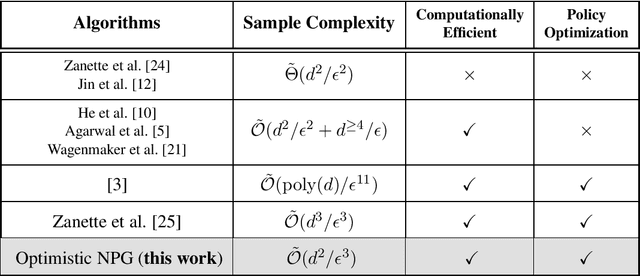
While policy optimization algorithms have played an important role in recent empirical success of Reinforcement Learning (RL), the existing theoretical understanding of policy optimization remains rather limited -- they are either restricted to tabular MDPs or suffer from highly suboptimal sample complexity, especial in online RL where exploration is necessary. This paper proposes a simple efficient policy optimization framework -- Optimistic NPG for online RL. Optimistic NPG can be viewed as simply combining of the classic natural policy gradient (NPG) algorithm [Kakade, 2001] with optimistic policy evaluation subroutines to encourage exploration. For $d$-dimensional linear MDPs, Optimistic NPG is computationally efficient, and learns an $\varepsilon$-optimal policy within $\tilde{O}(d^2/\varepsilon^3)$ samples, which is the first computationally efficient algorithm whose sample complexity has the optimal dimension dependence $\tilde{\Theta}(d^2)$. It also improves over state-of-the-art results of policy optimization algorithms [Zanette et al., 2021] by a factor of $d$. For general function approximation that subsumes linear MDPs, Optimistic NPG, to our best knowledge, is also the first policy optimization algorithm that achieves the polynomial sample complexity for learning near-optimal policies.

A Second-Order Method for Stochastic Bandit Convex Optimisation

We introduce a simple and efficient algorithm for unconstrained zeroth-order stochastic convex bandits and prove its regret is at most $(1 + r/d)[d^{1.5} \sqrt{n} + d^3] polylog(n, d, r)$ where $n$ is the horizon, $d$ the dimension and $r$ is the radius of a known ball containing the minimiser of the loss.

Optimistic Meta-Gradients

We study the connection between gradient-based meta-learning and convex op-timisation. We observe that gradient descent with momentum is a special case of meta-gradients, and building on recent results in optimisation, we prove convergence rates for meta-learning in the single task setting. While a meta-learned update rule can yield faster convergence up to constant factor, it is not sufficient for acceleration. Instead, some form of optimism is required. We show that optimism in meta-learning can be captured through Bootstrapped Meta-Gradients (Flennerhag et al., 2022), providing deeper insight into its underlying mechanics.

Generalization Bounds for Transfer Learning with Pretrained Classifiers

We study the ability of foundation models to learn representations for classification that are transferable to new, unseen classes. Recent results in the literature show that representations learned by a single classifier over many classes are competitive on few-shot learning problems with representations learned by special-purpose algorithms designed for such problems. We offer an explanation for this phenomenon based on the concept of class-features variability collapse, which refers to the training dynamics of deep classification networks where the feature embeddings of samples belonging to the same class tend to concentrate around their class means. More specifically, we examine the few-shot error of the learned feature map, which is the classification error of the nearest class-center classifier using centers learned from a small number of random samples from each class. Assuming that the classes appearing in the data are selected independently from a distribution, we show that the few-shot error generalizes from the training data to unseen test data, and we provide an upper bound on the expected few-shot error for new classes (selected from the same distribution) using the average few-shot error for the source classes. Additionally, we show that the few-shot error on the training data can be upper bounded using the degree of class-features variability collapse. This suggests that foundation models can provide feature maps that are transferable to new downstream tasks even with limited data available.

Understanding Self-Predictive Learning for Reinforcement Learning

We study the learning dynamics of self-predictive learning for reinforcement learning, a family of algorithms that learn representations by minimizing the prediction error of their own future latent representations. Despite its recent empirical success, such algorithms have an apparent defect: trivial representations (such as constants) minimize the prediction error, yet it is obviously undesirable to converge to such solutions. Our central insight is that careful designs of the optimization dynamics are critical to learning meaningful representations. We identify that a faster paced optimization of the predictor and semi-gradient updates on the representation, are crucial to preventing the representation collapse. Then in an idealized setup, we show self-predictive learning dynamics carries out spectral decomposition on the state transition matrix, effectively capturing information of the transition dynamics. Building on the theoretical insights, we propose bidirectional self-predictive learning, a novel self-predictive algorithm that learns two representations simultaneously. We examine the robustness of our theoretical insights with a number of small-scale experiments and showcase the promise of the novel representation learning algorithm with large-scale experiments.